
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм расчетов по методу молекулярной динамикиСодержание книги
Поиск на нашем сайте
Алгоритм включает следующие этапы. 1. Задание параметров, определяющих условия, при которых производится моделирование (например, начальная температура, количество частиц, плотность, временной шаг и т.д.). 2. Задаются начальные положения частиц и их скорости. 3. Рассчитываются силы, действующие на все частицы в системе. 4. Проводится интегрирование уравнений движения Ньютона. Этот шаг вместе с предыдущим составляет основу моделирования. Они повторяются до тех пор, пока не завершится расчет эволюции системы во времени на интересующем нас временном интервале. 5. После окончания главного цикла, вычисляются и выводятся средние значения рассчитываемых величин и происходит завершение программы. Рассмотрим теперь более подробно отдельные этапы алгоритма. Задание начальных значений параметров и положения частиц (инициализация)
Чтобы инициировать процесс моделирования необходимо задать начальные положения и скорости всех частиц в системе. Положения частиц должны быть выбраны совместимыми со структурой, которую мы стремимся воспроизвести. В любом случае частицы должны располагаться так, чтобы не было заметного перекрывания атомов и молекул. Часто это достигается за счет первоначального размещения частиц в узлах кубической решетки. Для задания начальных значений скоростей, каждой компоненте скорости, у каждой частицы, приписывается произвольное значение, с равномерным распределением, в интервале [- 0,5; 0,5]. атем производится сдвиг значений скоростей таким образом, чтобы суммарный импульс в системе стал равным нулю, а также проводится перемасштабирование скоростей для достижения желаемого значения средней кинетической энергии. В состоянии теплового равновесия выполняется следующее соотношение
где v α - α -я компонента скорости частицы. Соотношение (3) может быть использовано для определения мгновенной температуры T (t), в момент времени t:
Очевидно, что возможно подогнать значение мгновенной температуры T (t), к желаемому значению T, путем перемасштабирования всех скоростей, с коэффициентом Значения скоростей сами по себе не используются при решении уравнений Ньютона. Для предсказания положения частиц на следующем шаге используются положения частиц, в настоящий (X) и предыдущий (Xm) моменты времени, вместе с информацией о силах (f), действующих на частицу. В начале моделирования, для нормального выполнения алгоритма, необходимо искусственно задать положения частиц в предыдущий момент времени. Ограничиваясь учетом только закона сохранения импульса, можно оценить предыдущее положение частиц как:
Расчет сил
Расчет сил, действующих на каждую частицу, является наиболее трудоемким этапом моделирования методом молекулярной динамики. Если рассматривать модель системы с парными аддитивными взаимодействиями, необходимо учитывать вклад всех соседей рассматриваемой частицы. Если же рассматривать только взаимодействие между некоторой частицей и ближайшим образом другой частицы (периодические граничные условия), то для системы N частиц, необходимо вычислить N ·(N -1)/2, парных взаимодействий. Первоначально, необходимо рассчитать текущее расстояние в направлении x, y, z, для каждой пары частиц. Пусть это расстояние xr . При расчете межмолекулярных взаимодействий, с периодическими граничными условиями, используют обрезку потенциала, на расстоянии rc (где rc должен быть меньше половины диаметра периодической ячейки). В этом случае мы всегда можем свести расчет межмолекулярных взаимодействий между молекулами i и j, к взаимодействию между молекулой i, и ближайшим периодическим образом молекулы j. В случае использования простой кубической ячейки, с периодическими граничными условиями, расстояние в любом направлении, между i и ближайшим периодическим образом, молекулы j, всегда должно быть меньше (по абсолютной величине), чем половина диаметра периодической ячейки. Удобный способ вычислить расстояние между i и ближайшим периодическим образом j, заключается в использовании функции ближайшего целого, nint (x), которая округляет реальное число x, до ближайшего целого. Так, имея расстояние по x, между молекулами i и j, равное xr, расстояние, по x, между i, и ближайшим образом j, вычисляется как:
гдеbox – диаметр периодической ячейки. Вычислив, таким образом, все декартовы составляющие вектора расстояния r ij, между i и ближайшим периодическим образом j, определяется величина r ij 2. Далее проверяется будет ли r ij 2 меньше квадрата радиуса обрезки rc 2. Если нет, то сразу же производится переход к следующему значению. Если какие-либо две частицы расположены достаточно близко, чтобы они могли взаимодействовать друг с другом, тогда требуется рассчитать силы между этими частицами, а также вклад в потенциальную энергию. При этом, необходимо знать выражение для потенциальной энергии взаимодействия двух частиц, на расстоянии r. Так, x -составляющая силы fx (r), будет выражаться через потенциальную энергию взаимодействия u (r), в виде:
Рассмотрим пример взаимодействия молекул в неполярной жидкости. Энергия взаимодействия двух частиц в ней описывается потенциалом Ленард- Джонса (1924 год):
В уравнении (8) ε –глубина потенциальной ямы; σ – расстояние, на котором энергия взаимодействия становится равной нулю. Пример расчета сил взаимодействия в Леннард-Джонсовской жидкости
Выведем выражение для x -составляющей силы взаимодействия молекул, на расстоянии r. Введем безразмерные координаты: В новых переменных потенциал Леннард-Джонса примет вид:
Теперь x -составляющая силы взаимодействия fx молекул будет равна:
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

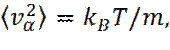 (3)
(3)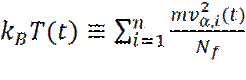 (4)
(4)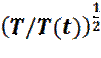 .
.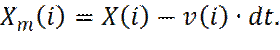 (5)
(5)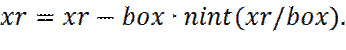 (6)
(6)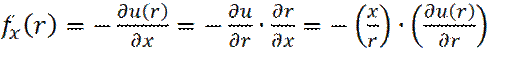 (7)
(7)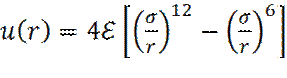 (8)
(8)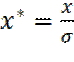 ,
, 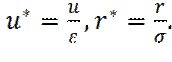
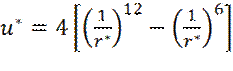 (9)
(9)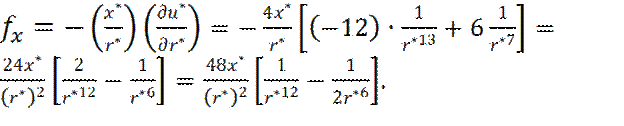 (10)
(10)


