
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика механической системыСодержание книги
Поиск на нашем сайте
Механическая система – это совокупность взаимодействующих между собой материальных точек (тел).
Классификация сил, действующих на материальные точки механической системы
– –
и реакции связей (реак-
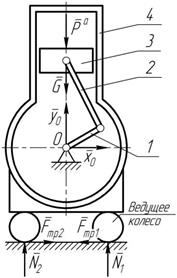
Рисунок 5.1 Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того какие тела входят в рассматриваемую систему. Например, рассмотрим механическую сис- тему (рисунок 5.1), состоящую из: кривошипа 1; шатуна 2; поршня 3; корпуса 4. Определим внешние и внутренние силы, активные и реакции связей (таблица 5.1).
Свойства внутренних сил: 1)
M j = å M (P j)= 0; 2)
Дифференциальные уравнения движения механической системы
dt 2 e + P j . (5.1)
дифференциальных уравнений. Для случаев, когда n > 3 решение уравнений имеют значительные математические трудности. Избежать этого помогут общие теоремы динамики для механической системы, основывающиеся на понятиях центра масс механической системы и момента инерции. Центр масс механической системы
масс m i всех точек (тел) входящих в эту систему (рисунок 5.2):
m = å m i .
Рисунок 5.2 Из статики известно (см. раздел I, тема 10, пункт 10.2):
Так как G = mg; G i = m i g, то = å r i G i .
C mg = å r i m i . (5.2)
Центром масс механической системы называется геометрическая точка C, радиус-вектор которой определяется равенством (5.2). В проекции на координатные оси получим: x C m y C m z C m Осевые моменты инерции твердого тела Характер распределения массы тел относительно плоскости, оси или центра существенно влияет на движение этих тел (системы тел) и характеризуется соответствующим моментом инерции. Ограничимся рассмотрением моментов инерции относительно оси (рисунок 5.3).
Рисунок 5.3
Для тонкостенного кольца (рисунок 5.4) рас-
есть величина постоянная равная R:
= mR 2.
Рисунок 5.4 Момент инерции любого тела можно представить в виде:
где r = i z – радиус инерции – расстояние от оси вращения, на котором необходимо разместить массу тела, чтобы момент инерции размещенной массы равнялся моменту инерции тела относительно этой оси, м. Для сложных тел, для которых момент инерции математически выразить затруднительно, определяется и задается именно радиус инерции. Момент инерции тела относительно оси проходящей через его центр масс (центральной оси) всегда наименьший.
Теорема Гюйгенса-Штейнера (рисунок 5.5)
расстояния между этими осями:
J z = J z + md 2. Моменты инерции некоторых однородных тел 1. Тонкий стержень (рисунок 5.6)
r. Его масса определится: m = r V = r Fl, Рисунок 5.6 где V – объем тела, м3. Разобьем стержень на элементарные участки длиной D x i, массы которых m i = r F D x i . Тогда момент инерции относительно оси z, проходящей перпендикулярно стержню через его край, будет равен: J = å m x 2 = å r F x 2D x = r F å x 2D x. z i i i i i i Перейдя к пределу суммы, получаем определенный интеграл: l r Fl 3 l 2 ml 2
0 3 3 3 С помощью теоремы Гюйгенса-Штейнера определим момент инерции
C относительно центральной оси z C параллельной оси z:
C = ml 2
- ml 2
ml 2
12
.
Момент инерции тонкого стержня относительно оси дящей через центр масс:
z C, прохо-
2. Круглый диск малой толщины и цилиндр (рисунок 5.7)
имеет весьма малую толщину h и плотность r. m = r V = r hF = r h p R 2. Разобьем диск на элементарные кольца шириной
Рисунок 5.7 D r i, массы которых m i = r hF i. æ D r ö2 æ D r ö2 F i = p ç r i + i ÷ - p ç r i - i ÷ = 2 p r i D r i; è 2 ø è 2 ø m i = 2 r h p r i D r i.
Перейдя к пределу суммы, получаем определенный интеграл:
= r h p R 2
mR 2
Момент инерции круглого диска относительно оси z: mR 2 J z = . (5.3)
инерции инерций J z D J z определим как сумму моментов элементарных пластинок толщиной
Рисунок 5.8 пользуясь формулой (5.3):
R 2 å
mR 2
. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ Теорема о движении центра масс механической системы
m P dt 2 e + å P j;
e j
Согласно свойству внутренних сил
å P j = 0, с учетом уравнения (5.2)
m P e ; dt 2
C i т.е. произведение массы механической системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил.
Центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы, и к которой приложены все внешние силы, действующие на систему.
Если å P e = R e = 0, то центр масс механической системы находится в покое или движется равномерно прямолинейно: u C = const. Теорема об изменении количества движения Количество движения – векторная мера, характеризующая способность одних тел передавать движение другим телам тоже в виде механического движения.
Рисунок 6.1 Запишем 2-й закон динамики в диф- ференциальном виде для движущейся под действием силы P материальной точки M (рисунок 6.1):
dt
dt
– количество движения материальной точки, кг × м.
Тогда получим:
dq = P. (6.2)
Производная по времени от количества движения материальной точки равна силе, приложенной к этой точке.
(u ) (t )
¾ п ¾ р и t ¾0 =0¾® q - q 0 = S, где
S = ò Pdt (t) – импульс силы P за промежуток времени t - t 0, Н× с.
Изменение количества движения материальной точки за конечный промежуток времени равно импульсу силы, приложенной к материальной точке, за тот же промежуток времени.
Количество движения механической системы Q равно геометриче-
ее точек:
r C m = å r i m i
, получим, что Q = m dr C
= m u C.
Найдем производную по времени от Q:
C i
dQ = å P e . (6.3)
внешних сил e равен нулю, то

количество движения механической системы Q остается неизменным:
= å S e. Изменение количества движения механической системы за конечный промежуток времени равно геометрической сумме импульсов всех внешних сил приложенных к механической системе, за тот же промежуток времени. Теорема об изменении момента количества движения
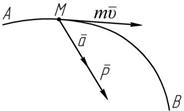
    M O (P)= r ´ P. M O (P)= r ´ P.
Момент количества движения L O
относительно этого же центра будет соответственно равен:
M O (m u) = L O = r ´ m u,
é кг × м2 ù
Найдем производную по времени от ë û
L O:
dL O = d (r ´ m u) = dr ´ m u + r ´ d ( mu ) = u ´ m u + r ´ ma.
Так как векторы u и m u направлены по одной прямой, то
= r ´ P = M O (P). (6.4) Производная по времени от момента количества движения материальной точки относительно произвольного неподвижного центра равна моменту силы, действующей на материальную точку, относительно того же центра. Кинетический момент механической системы
K O равен
геометрической сумме моментов количеств движения
L iO ее точек:
Тогда просуммировав выражение (6.4), с учетом того что
(P e ).
dt = å M (P e ). (6.5)
Дифференциальное уравнение вращательного движения твердого тела Определим кинетический момент твердого тела относительно оси его вращения (оси z), рассмотрев движение точки M i массой m i, принадлежащей телу и движущейся в плоскости перпендикулярной оси z на расстоянии r i (рисунок 6.3).
относительно оси z будет равен: L iz = m i u i r i. Так как u i = w r i, то L = m w r 2. iz i i Тогда кинетический момент определится: K = å L = å m w r 2 = w å m r 2 = J w. Рисунок 6.3 z iz i i i i z Производная от кинетического момента по времени будет равна: dK z = d (J w) = J dw.
dt dt z z dt С учетом уравнения (6.5) получим: J dw = å M (P e )
J e = å M (P e ). (6.6)
z z i Произведение момента инерции твердого тела относительно оси вращения на производную по времени от угловой скорости его вращения равно сумме моментов всех внешних сил, действующих на тело, относительно той же оси. Из выражения (6.6) видно, что момент инерции во вращательном движении играет ту же роль, что и масса тела при поступательном движении, т.е. является мерой инертности тела.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.169 (0.01 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Силы, действующие на механическую сис- тему, разделяют на:
Силы, действующие на механическую сис- тему, разделяют на:

 Таблица 5.1 – Разделение сил, действующих на механическую систему
Таблица 5.1 – Разделение сил, действующих на механическую систему Для механической системы, состоящей из n материальных точек, можно составить n векторных дифференциальных уравнений движений:
Для механической системы, состоящей из n материальных точек, можно составить n векторных дифференциальных уравнений движений: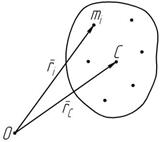 Масса механической системы m равна сумме
Масса механической системы m равна сумме
 G
G

 r = å r i m i g =
r = å r i m i g =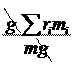

 m
m = å x i m i;
= å x i m i; = å y i m i;
= å y i m i; = å z i m i.
= å z i m i.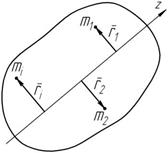 Момент инерции тела относительно оси – это сумма произведений массы каждой точки тела на квадрат расстояния от оси до точки:
Момент инерции тела относительно оси – это сумма произведений массы каждой точки тела на квадрат расстояния от оси до точки: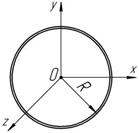 стояние r i
стояние r i Момент инерции тела относительно любой оси равен моменту инерции тела относительно параллельной оси, проходящей через центр его масс плюс произведение массы тела на квадрат
Момент инерции тела относительно любой оси равен моменту инерции тела относительно параллельной оси, проходящей через центр его масс плюс произведение массы тела на квадрат Предположим, что стержень длиной l имеет постоянное весьма малое сечение F и плотность
Предположим, что стержень длиной l имеет постоянное весьма малое сечение F и плотность

 J z = r F ò x 2 dx = = r Fl = .
J z = r F ò x 2 dx = = r Fl = . 3
3
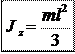 Момент инерции тонкого стержня относительно оси z:
Момент инерции тонкого стержня относительно оси z: .
. Предположим, что круглый диск радиусом R
Предположим, что круглый диск радиусом R J z = 2 r h p ò r 3 d r = 2 r h p
J z = 2 r h p ò r 3 d r = 2 r h p .
.
 2
2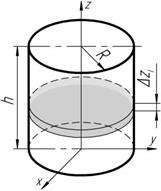 Для круглого цилиндра (рисунок 5.8) момент
Для круглого цилиндра (рисунок 5.8) момент


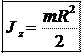 Момент инерции круглого цилиндра относительно оси z:
Момент инерции круглого цилиндра относительно оси z: Суммируя уравнение (5.1) получим:
Суммируя уравнение (5.1) получим:



 где m u = q
где m u = q с
с


 dt
dt dQ = d (m u C ) = m d u C dt dt dt
dQ = d (m u C ) = m d u C dt dt dt Пусть материальная точка M движется под действием силы P (рисунок 6.2). Момент этой силы относительно произвольного неподвижного центра O определится:
Пусть материальная точка M движется под действием силы P (рисунок 6.2). Момент этой силы относительно произвольного неподвижного центра O определится: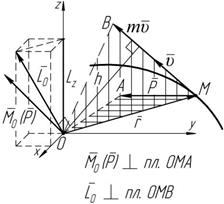 Рисунок 6.2
Рисунок 6.2 [ L O ] = ê с ú .
[ L O ] = ê с ú .


 dK O dt
dK O dt dK z
dK z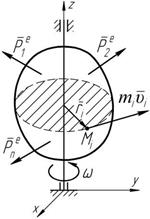 Момент количества движения точки M i
Момент количества движения точки M i



