
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр тяжести. Координаты центра тяжестиСодержание книги
Поиск на нашем сайте
Центр параллельных сил
Рассмотрим систему параллель- ных сил
P 1,
P 2, …,
P n, приложенных в Рисунок 10.1 точках B 1, B 2, …, B n, приводящуюся к
равнодействующей R, приложенной в точке C (рисунок 10.1). На основании теоремы Вариньона запишем:
В свою очередь M O (R)= r C ´ R;
C R
u P i, тогда после преобразований
R = å P i = u å P i = u R;
r C ´ u R = å r i ´ u P i ; r C R ´ u = å r i P i ´ u;
C R В проекции на координатные оси получим:
C R y = å y i P i;
z = å z i P i.
Центр тяжести твердого тела Вблизи поверхности Земли линии действия векторов сил тяжестей отдельных тел можно считать параллельными, так как на расстоянии 31 м угол между ними равен 0°01¢ . Центр тяжести тела – фиксированная в данном теле точка, через которую проходит равнодействующая параллельных сил тяжести всех частиц этого тела при любом положении тела. Необходимо отметить, что эта точка не обязательно будет принадлежать самому телу.
ность бесконечно малых объемов каждый из которых имеет свой вес G i. Если тело однородное, то: V i,
Рисунок 10.2 G = g V, G i = g V i ,
Согласно пункту (10.1): где V – объем тела, м3; g – вес единицы объема
Н/м3.
C G или в проекции на декартовы оси координат
C G y = å y i G i;
z = å z i G i,
где x i, y i, z i – координаты центров тяжестей элементарных объемов, м.
Тогда x = å x i G i = å x i g V i = g å x i V i = å x i V i.
C G g V g V V
C V y = å y i V i;
z = å z i V i.
Центр тяжести плоской фигуры
определяется двумя координатами x C, y C. Разобьем фигуру (рисунок 10.3) на элементар- ные площадки B i весом G i и площадью F i. Вес
Рисунок 10.3
где F – площадь фигуры, фигуры определится по формуле G = n F, а вес каждой площадки G i = n F i, м2;
Тогда x = å x i G i = å x i n F i = n å x i F i = å x i F i .
C G n F
C F
C F где x i, y i – координаты центров тяжестей элементарных площадок, м.
Рисунок 10.4 Центр тяжести линии
Вес линии выразим формулой G = rL, где r – вес единицы длины линии, Н/м; L – длина линии, м.
и весом G i = r l i.
Тогда x = å x i G i = å x i r l i = r å x i l i = å x i l i .
C G r L r L L
y = å y i l i; C L z = å z i l i, C L
x i, y i, z i – координаты центров тяжестей элементарных участков, м.
Методы определения центра тяжести Метод симметрии Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
2. Сложная фигура разбивается на совокупность простых фигур, для которых известны положения центра тяжести или легко определяются:
= x 1 F 1 + x 2 F 2.
C å F F + F Рисунок 10.5
3. Метод отрицательных площадей (рисунок 10.6)
Например, вместо разбиения фигуры на 4 обычных прямоугольника, ее можно представить как совокупность двух прямоугольников, один из Рисунок 10.6 которых имеет отрицательную площадь:
= x 1 F 1 + x 2 (- F 2 ) .
C å F F + (- F) Метод интегрирования Выполняется аналитическое интегрирование или численные методы интегрирования. Используется при наличии у фигуры контура описы- ваемым известным уравнением.
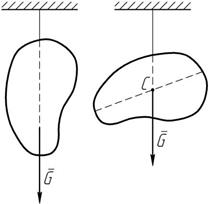
5. Метод подвешивания (экспериментальный) (рисунок 10.7)
Для определения положения центра C тяжести плоской фигуры достаточно подве- сить ее поочередно за две любые точки и Рисунок 10.7 прочертить соответствующие вертикали, на- пример, с помощью отвеса, и точка пере- сечений этих прямых соответствует положению центра тяжести фигуры.
6. Метод взвешивания (экспериментальный) (рисунки 10.8–10.10) Этот метод применяется для определения центра тяжести сложных объемных тел. Пример. Определить центр C тяжести грузовика по заданным его геометрическим параметрам (AB, HD, d). 1. Определим вес грузовика, взвешивая поочередно переднюю ось и заднюю ось. При этом узнаем вес, приходящийся на каждую ось грузовика
алгебраической сумме:
G = G A + G B.
2. Определим плоскость действия силы G. Взвесив заднюю ось (рисунок 10.8), определили модуль реакции
N B.
3.
 
Пересечение полученных плоскостей определяет прямую ab, на которой лежит центр тяжести C грузовика. 4.
Для определения положения центра тяжести (точки C) на прямой ab, повторим опыт, но при этом расположим грузовик, как показано на рисунке 10.10. При этом: å M L (P i )= - G l 3 + N K d = 0.
Тогда определим удаление l 3
плоскости действия силы G от линии
действия N L (плоскость yOz, которая в плоскости xOz изображена
РАЗДЕЛ II. КИНЕМАТИКА Кинематика – раздел механики, изучающий движение материальных точек (тел) в пространстве с геометрической точки зрения, без учета их масс и сил вызывающих это движение. Материальная точка – точка имеющая массу. Тело конечной массы, размерами и различием движения отдельных точек которого можно пренебречь в условиях данной задачи, принимают за материальную точку. Движущаяся точка описывает в пространстве некоторую линию – геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета. Эта линия называется траекторией точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Изучение движения точки заключается в определении основных кинематических параметров этого движения: положение точки, ее скорость и ускорение. Эта задача решается различными способами. Существуют три основных способа задания движения точки: – векторный; – координатный; – естественный. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ Векторный способ задания движения
однозначной, непрерывной и Рисунок 1.1 дважды дифференцируемой:
Кривая AB – траектория точки. Линия, образованная концами переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора.
Скорость – векторная величина, характеризующая изменение положения точки в единицу времени.
точка переместилась из положения
M 1 (рисунок 1.1). Отношение вектора перемещения D r к промежутку времени D t представляет собой вектор средней скорости u ср воображаемого движения точки по хорде MM 1: u ср = D r.
u ср направлен так же, как вектор D r. При
его направление стремится к направлению касательной, проведенной из точки M в сторону движения точки. Для определения вектора скорости точки в момент времени t переходим к пределу:
D t ®0 D t dt
Вектор скорости u направлен по касательной к траектории в сторону движения точки.
Годограф скорости – линия, которую описывают точки концов векторов скорости, отложенных из одного центра O 1 (рисунок 1.2).
Рисунок 1.2 Уравнения годографа скорости показаны в пункте 1.2.
Ускорение – векторная величина, характеризующая изменение скорости по величине и направлению в единицу времени.
точка переместилась из положения M в
M 1 , и вектор скорости
Рисунок 1.3 изменился на величину (рисунок 1.3). D u = u 1 - u Разделив приращение вектора скорости D u на промежуток времени D t, получим вектор среднего ускорения точки за этот промежуток времени:
= D u. D t Вектор среднего ускорения будет сонаправлен с направлением приращения вектора скорости D u. Покажем это на годографе скорости.
a ср, когда D t ® 0, является вектором ускорения точки в данный момент времени t:
= du; D t ®0 D t dt Учитывая, что скорость является вектор-функцией от времени
dt
, получим: a = du = d æ dr ö = d r = ¢¢
 
dt dt ç dt ÷ dt 2 r. (1.3)
Вектор ускорения в данный момент равен первой производной от вектора скорости или второй производной от радиус-вектора по времени. Вектор ускорения лежит в соприкасающейся плоскости и направлен по касательной к годографу скорости в сторону вогнутости траектории.
Координатный способ задания движения Положение точки в пространстве определяется координатами x, y, z, являющиеся функциями времени (рисунок 1.4):
y = f 2 (t )ý . (1.4) ï
f 1 (t), f 2 (t) и f 3 (t)
Рисунок 1.4 должны быть однозначными, непре- рывными и дважды дифференци- руемыми. Уравнения (1.4) являются уравнениями движения точки, а так же уравнениями траектории точки в параметрической форме, так как зависят от параметра t. Чтобы получить уравнения траектории в координатной форме, необходимо из уравнений (1.4) исключить параметр t:
t = f (x) Þ y = f 2 éë f (x)ûùïü
z = f 3 éë f (x)ùû ïþ
Пример. Определить уравнение траектории точки, если она движется в плоскости xy по закону: x = 4 t 2; y = 10 t 2.
Тогда уравнение траектории определим разделив уравнения друг на друга:
Þ y = 2,5 x, x 4 t 2 или подстановкой, выраженного из уравнения x = 4 t 2 значения t 2, в уравнение y = 10 t 2:
x = 4 t 2
è ø
Þ t 2 = x;
Þ y = 2,5 x.
= xi + yj + zk,
соответствующих осей x, y, z;
Скорость точки Согласно теореме: проекция производной от вектора на ось, неподвижную в данной системе отсчета, равна производной от проекции дифференцируемого вектора на ту же ось, – запишем:
= dx i
+ dy
j + dz k
= u i + u
x y z
u = dy = y;
u = dz = z. (1.5)
x dt y dt z dt Проекции скорости точки на неподвижные декартовые оси координат равны первым производным от соответствующих координат точки по времени.
. (1.6)
cos(u, u x cos(u, u = cos a = u x ;
)= cos b = u y ;
y cos(u, u z )= cos g u
u
ì x Г ï
= u x (t ) = x (t ); = u y (t) = y (t);
f 1 (t ) ü
u = f é f (u )ùü u y = f 2 (t)ý;
t = f (u x ) Þ y u z = 2 ë x f 3 éë f (u x ûï. þ
Пример. Определить уравнение годографа скорости, если точка движется в плоскости xy по закону: x = 5 t 2 + 2 t; y = 2 t 3 -1.
Определим проекции скорости на координатные оси:
x dt
y dt Таким образом, получили уравнения годографа скорости в параметрической форме: ìï u x = 10 t + 2;
= 6 t 2.
Исключив параметр t, получим уравнение годографа скорости, т.е. уравнение вида u y = f (u x ): u - 2
æ u - 2 ö2 t = x Þ u y = 6ç x ÷ ; 10
è 10 ø - 2)2 . y 50 Ускорение точки Так как a = du , а u = u i + u j + u k, тогда
+ d u y j + d u z k.
a = d u y y dt
a = d u z z dt
. (1.8)
Направление вектора ускорения определяется направляющими косинусами (рисунок 1.5):
= cos a = a x;
= cos b = a y;
Рисунок 1.5 cos(a, a z )= cos g = a z.
Естественный способ задания движения
1) траекторию точки (AB), т.е. уравнение траектории x = f ( y, z);
Рисунок 1.6 2) начало отсчета (точка O) с указанием направления движения («+» и «»); 3) закон движения s = f (t) – дуговая координата в функции времени,
которая должна быть однозначна, непрерывна и дважды дифференцируема. Следует различать путь и дуговую координату. Дуговая координата определяет положение точки на траектории относительно начала отсчета (точки O, см. рисунок 1.6). Путь – расстояние пройденное точкой за некоторый промежуток времени вдоль траектории. Допустим, за время t 1 точка переместилась из начального положения M 0 в положение M 1 (рисунок 1.5), а за время t 2 из M 1 в точку O (таблица 1.1).
Таблица 1.1 – Отличие дуговой координаты от пути
При естественном способе задания движения вводится система взаимно перпендикулярных осей (t, n, b), движущихся вместе с точкой и меняющих свое положение в пространстве – естественная система координат (рисунок 1.7).
Рисунок 1.7 b = t ´ n. Орт t направлен по касательной к траектории в сторону увеличения дуговой координаты.
При движении точки, траектория всегда находится в соприка- сающейся плоскости, образованной осями t и n.
Скорость точки
× ds = ds × dr
. (1.9)
направлен также, как
(рисунок 1.8). При D s ® 0
Рисунок 1.8 его направление стремится к направ- лению касательной, проведенной из точки M в сторону увеличения дуговой координаты s. Модуль этого вектора стремится к единице:
dr = lim D r = lim MM 1 = 1.
Таким образом, вектор dr
имеет модуль, равный единице, и направлен по касательной к траектории в сторону увеличения дуговой
координаты. Вектор dr
является ортом t этого направления:
dr = t.
Тогда уравнение (1.9) примет вид:
dt
dt
есть проекция вектора скорости на касательную ось t, т.е. определяет алгебраическую величину
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.143.149 (0.008 с.) |

 Центр параллельных сил – точка приложения равнодействующей, не изменяющей своего положения при одновременном повороте всех сил на один и тот же угол.
Центр параллельных сил – точка приложения равнодействующей, не изменяющей своего положения при одновременном повороте всех сил на один и тот же угол.






 r = å r i ´ P i .
r = å r i ´ P i . Если ввести единичный вектор
Если ввести единичный вектор



 r = å r i P i .
r = å r i P i . x = å x i P i;
x = å x i P i; C R
C R C R
C R Рассмотрим тело произвольной формы с центром тяжести в точке C (рису- нок 10.2). Представим тело, как совокуп-
Рассмотрим тело произвольной формы с центром тяжести в точке C (рису- нок 10.2). Представим тело, как совокуп-
 r = å r i G i ,
r = å r i G i , x = å x i G i;
x = å x i G i; C G
C G C G
C G



 x = å x i V i;
x = å x i V i; C V
C V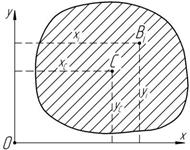 Положение центра тяжести плоской фигуры
Положение центра тяжести плоской фигуры n – вес единицы площади фигуры, Н/м2.
n – вес единицы площади фигуры, Н/м2.
 x = å x i F i ;
x = å x i F i ;
 n F F
n F F y = å y i F i,
y = å y i F i,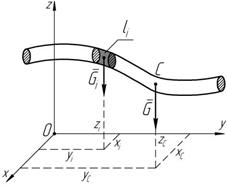 Определим положение центра тяжести однородного тела, имеющего большую протяженность при сравнительно малой площади поперечного сечения, т.е. линии (рисунок 10.4).
Определим положение центра тяжести однородного тела, имеющего большую протяженность при сравнительно малой площади поперечного сечения, т.е. линии (рисунок 10.4).

 Разобьем линию на элементарные участки длиной l i
Разобьем линию на элементарные участки длиной l i
 x = å x i l i; C L
x = å x i l i; C L
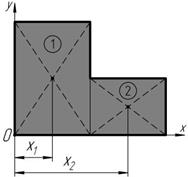 Метод разбиения (рисунок 10.5)
Метод разбиения (рисунок 10.5)

 Так же, как и в методе разбиения, сложная фигура разбивается на совокупность простых фигур, но отверстия или пустоты представляют в виде «отрицательных» областей.
Так же, как и в методе разбиения, сложная фигура разбивается на совокупность простых фигур, но отверстия или пустоты представляют в виде «отрицательных» областей.

 Основан на том, что при подвешивании тела за какую-либо произвольную точку центр тяжести находится на одной вертикали с точкой подвеса.
Основан на том, что при подвешивании тела за какую-либо произвольную точку центр тяжести находится на одной вертикали с точкой подвеса. (G A = - N A и G B = - N B ). Вес G всего грузовика будет равен
(G A = - N A и G B = - N B ). Вес G всего грузовика будет равен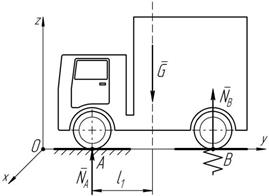 Рисунок 10.8
Рисунок 10.8
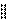 xOz):
l = N B AB.
1 G
xOz):
l = N B AB.
1 G
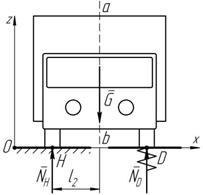 Рисунок 10.9
Рисунок 10.9


 линией fe):
линией fe): Рисунок 10.10
Рисунок 10.10
 Положение точки M в пространстве определяется радиус- вектором r, проведенным из некоторого неподвижного центра O в данную точку M (рисунок 1.1).
Положение точки M в пространстве определяется радиус- вектором r, проведенным из некоторого неподвижного центра O в данную точку M (рисунок 1.1). r = f (t ). (1.1)
r = f (t ). (1.1) Пусть за промежуток времени D t
Пусть за промежуток времени D t M в положение
M в положение D t
D t

 Годограф скорости. Ускорение
Годограф скорости. Ускорение Пусть за промежуток времени D t
Пусть за промежуток времени D t
 u = f (t) и что u = dr
u = f (t) и что u = dr


 Функции
Функции
 y = 10 t 2
y = 10 t 2
 4
4
 x, y, z – проекции радиус-вектора r на неподвижные координатные оси.
x, y, z – проекции радиус-вектора r на неподвижные координатные оси.


 dt dt dt dt
dt dt dt dt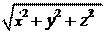 По модулю скорость будет равна:
По модулю скорость будет равна: u = =
u = = u
u = u z.
= u z. Уравнения годографа скорости (рисунок 1.2) в параметрической форме можно записать в виде:
Уравнения годографа скорости (рисунок 1.2) в параметрической форме можно записать в виде: u = 3(u x
u = 3(u x

 a = d u x x dt
a = d u x x dt = x;
= x; = y;
= y; = z. (1.7)
= z. (1.7)
 Проекции ускорения точки на неподвижные декартовые оси координат равны вторым производным от соответствующих координат точки по времени.
Проекции ускорения точки на неподвижные декартовые оси координат равны вторым производным от соответствующих координат точки по времени. По модулю ускорение будет равно:
По модулю ускорение будет равно:
 a = =
a = =


 a
a Для задания движения естественным способом необходимо знать (рисунок 1.6):
Для задания движения естественным способом необходимо знать (рисунок 1.6): Совокупность взаимно перпендику- лярных плоскостей, определяемых осями этой системы, называют подвижным трехгранником.
Совокупность взаимно перпендику- лярных плоскостей, определяемых осями этой системы, называют подвижным трехгранником. dt ds dt ds
dt ds dt ds Вектор D r
Вектор D r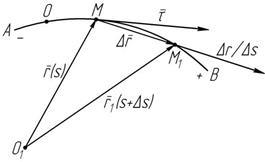 D s
D s

 ds
ds ds
ds ds
ds u = ds t.
u = ds t. Производная ds
Производная ds


