
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы относительно центра, точки и осиСодержание книги
Поиск на нашем сайте
В дальнейшем «центром» будем называть точку в пространстве, а «точкой» – точку на плоскости.
 – векторная величина, равная векторному произведению радиуса-вектора, проведен- ного из этого центра в точку приложения силы, на вектор силы: – векторная величина, равная векторному произведению радиуса-вектора, проведен- ного из этого центра в точку приложения силы, на вектор силы:
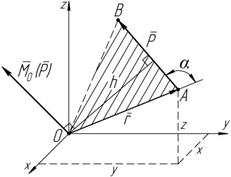
M O (P)= r ´ P. Рисунок 3.1 Вектор M O (P) (рисунок 3.1) приложен
   в центре O и направлен перпендикулярно плоскости OAB, в такую сторону, чтобы, смотря ему навстречу, видеть силу P стремящуюся вращать плоскость OAB против хода часовой стрелки. в центре O и направлен перпендикулярно плоскости OAB, в такую сторону, чтобы, смотря ему навстречу, видеть силу P стремящуюся вращать плоскость OAB против хода часовой стрелки.
По модулю момент силы P относительно центра O будет равен:
M O (P)= r ´ P = r P sin (r, P)= P r sin a = P h, Размерность момента силы [H × м]. Момент силы относительно точки – произведение модуля силы на плечо:
– момент силы P относительно точки A.
Плечом (h) называется кратчайшее расстояние от точки (полюса), относительно которой определяем момент, до линии действия силы.
1) значение момента силы не изменится, если силу переместить вдоль линии ее действия в любую точку; 2) момент силы относительно точки (центра) равен нулю, если линия действия силы проходит через полюс.
Момент силы относительно оси (рисунок 3.3). Чтобы найти момент
 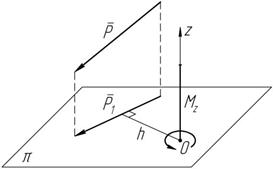 силы P относительно оси z, необходимо спроецировать силу на плоскость p (плоскость вращения), перпендикулярную оси вращения z, и силы P относительно оси z, необходимо спроецировать силу на плоскость p (плоскость вращения), перпендикулярную оси вращения z, и
найти момент полученной проекции P 1
Рисунок 3.3 относительно точки O пересечения оси с плоскостью. Момент силы относительно оси – произведение модуля проекции
относительно точки O пересечения оси с плоскостью: M z = P 1 h.
Момент силы относительно оси равен нулю, когда: 1) линия действия силы параллельна оси, относительно которой определяется момент силы; 2) линия действия силы пресекает ось, относительно которой определяется момент силы; т.е. момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости.
Теорема Вариньона о моменте равнодействующей Момент равнодействующей системы сил относительно какого-либо центра равняется геометрической сумме моментов сил, составляющих эту систему, относительно того же центра:
– относительно центра O.
Момент равнодействующей системы сил относительно точки или оси равен алгебраической сумме моментов сил, составляющих эту систему, относительно той же точки или оси:
– относительно оси x.
будет равен:
Рисунок 3.4
Так как M A (P)= r ´ P.
 Если силу P разложить на составляющие, то момент этой силы относительно точки A будет равен алгебраической сумме моментов этих составляющих относительно той же точки: Если силу P разложить на составляющие, то момент этой силы относительно точки A будет равен алгебраической сумме моментов этих составляющих относительно той же точки:
M A (P)= - P x × h + P y × d = - P cos a × h + P sin a × d.
Уравнение линии действия равнодействующей плоской системы сил
образом, что его проекции
R x и R y на
Рисунок 3.5 координатные оси x и y направлены в стороны положительных направлений соответствующих осей. Согласно теореме Вариньона:
P 1 =10 Н, P = 8 Н, P 3 =18 Н, P =14 Н,
Рисунок 3.6 a = 3 м, b = 4 м. Сначала определяем проекции равно- действующей на координатные оси: R x = å P i x = P 1 - P 3 =10 -18 = -8 Н; R y = å P i y = - P 2 + P 4 = -8 +14 = 6 Н.
Далее определяем сумму моментов всех сил относительно произволь- ной точки, например, относительно начала координат (точки O): å M O (P i )= - P 1 b - P 2 a + P 3 b + P 4 a;
Так как å M O (P i )= M O (R), согласно формуле (3.1), получим:
50 = 6 x - (-8) y; 6 x + 8 y - 50 = 0; 3 x + 4 y - 25 = 0. (3.3)
R
По величине сила R будет равна:
Тогда кратчайшее расстояние d от моментной точки O до линии
действия силы R составит:
R 10 ТЕОРИЯ ПАР СИЛ Сложение двух параллельных сил
P 1 и
P 2 одного направления (рисунок 4.1) имеет такое же
Рисунок 4.1 направление, а ее модуль равен алгебраической сумме модулей слагаемых сил: R = P 1 + P 2 . Точка C приложения равнодействующей делит отрезок AB на части обратно пропорциональные модулям сил:
BC P 1 По свойству пропорций: P 1
= P 2 =
P 1 + P 2
BC AC BC + AC Откуда следует равенство:
= R . (4.1)
Равнодействующая R двух параллельных сил
P 1 и
P 2 противоположного направления (рисунок 4.2) имеет
направление силы, большей по модулю, и модуль, равный разности модулей этих сил: R = P 1 - P 2 . Точка C приложения равнодействующей лежит на продолжении отрезка AB за точкой приложения большей силы:
= R . (4.2)
Пара сил. Момент пары сил
Пара сил – это самостоятельный, не
Рисунок 4.3
1) плоскостью действия; 2) направлением вращения; упрощаемый элемент статики, харак- теризующийся: 3) модулем (величиной) момента пары.
где h – кратчайшее расстояние между линиями действия сил, состав- ляющих пару, м. Размерность момента пары сил [H × м].
изображают вектором M, который
перпендикулярен плоскости действия пары и направлен в ту сторону, откуда видно пару сил стремящуюся вращать плоскость ее действия против хода часовой стрелки. Момент пары сил считается положительным «+», если пара сил стремится вращать плоскость в сторону противоположную ходу часовой стрелки, и отрицательным «» – если в сторону хода часовой стрелки.
Свойства пар Проекция пары на любую ось равна нулю, что следует из определения пары сил. Не изменяя действия пары на твердое тело, пару можно перемещать и поворачивать в плоскости ее действия, переносить в любую плоскость, параллельную плоскости действия пары, а так же изменять ее силы и плечо, сохраняя неизменным модуль и направление момента пары. Таким образом, момент пары сил, есть вектор свободный, т.е. не имеющий определенной точки приложения.
Сложение пар, лежащих в пересекающихся плоскостях Заменим сходящиеся силы в точках A и B их равнодействующими (рисунок 4.4):
= и P 2 P 1 + P 2 = R;
M 2 (P 2 , P 2¢)= A B ´ P 2 .
Рисунок 4.4
При сложении нескольких пар получим:
(P 2 , P 2¢), лежащие в пере- секающихся плоскостях,
момент которой равен геометрической сумме мо- ментов слагаемых сил:
M = A B ´ P 1 + A B ´ P 2 .
Если тело под действием системы пар находится в равновесии, то момент результирующей пары равняется нулю: M = å M i = 0. В проекции на оси координат получим:
ïîå M i z = 0. Если пары расположены в одной плоскости, векторы моментов их будут параллельны. Момент результирующей пары определится как алгебраическая сумма моментов пар: M = å M i .
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 Момент силы относительно центра
Момент силы относительно центра




 M A (P)= ± Ph
M A (P)= ± Ph
 Момент силы считается положительным «+», если мы условно видим обход заданного вектора силы P вокруг полюса (точки A) против хода часовой стрелки, и отрицательным «» – если по ходу часовой стрелки.
Момент силы считается положительным «+», если мы условно видим обход заданного вектора силы P вокруг полюса (точки A) против хода часовой стрелки, и отрицательным «» – если по ходу часовой стрелки.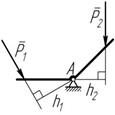 Рисунок 3.2
Рисунок 3.2
 Свойства момента силы относительно точки (центра):
Свойства момента силы относительно точки (центра):

 M x (R)= å M x (P i )
M x (R)= å M x (P i )
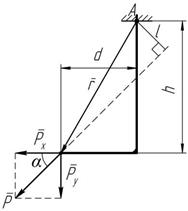 Пример (рисунок 3.4). Пусть к телу приложена сила P. Определить момент этой силы относительно точки A.
Пример (рисунок 3.4). Пусть к телу приложена сила P. Определить момент этой силы относительно точки A. Момент силы P относительно точки A
Момент силы P относительно точки A


 По модулю момент силы P относительно точки A будет равен:
По модулю момент силы P относительно точки A будет равен: M A (P)= - P × l.
M A (P)= - P × l.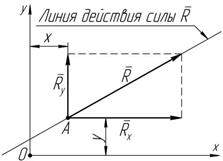 Пусть равнодействующая R плоской системы сил приложена в точке A (рисунок 3.5). Вектор R расположен таким
Пусть равнодействующая R плоской системы сил приложена в точке A (рисунок 3.5). Вектор R расположен таким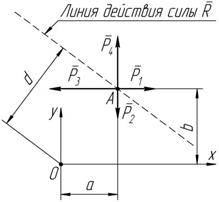 Пример. Определить уравнение линии действия равнодействующей R плоской
Пример. Определить уравнение линии действия равнодействующей R плоской d .
d .
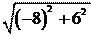 R = = = 10 Н.
R = = = 10 Н.

 d 5 м
d 5 м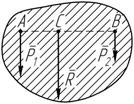 Равнодействующая R двух параллельных сил
Равнодействующая R двух параллельных сил
 AC = P 2.
AC = P 2.



 P 1 = P 2
P 1 = P 2 BC AC AB
BC AC AB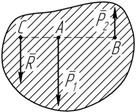 Рисунок 4.2
Рисунок 4.2
 P 1 = P 2
P 1 = P 2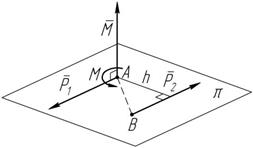 Пара сил – совокупность двух равных по модулю параллельных сил, направленных в противоположные стороны (рисунок 4.3).
Пара сил – совокупность двух равных по модулю параллельных сил, направленных в противоположные стороны (рисунок 4.3).
 P 2 = - P 1 ; P 1 P 2 .
P 2 = - P 1 ; P 1 P 2 .


 Так как
Так как







 R = R ¢ .
R = R ¢ .
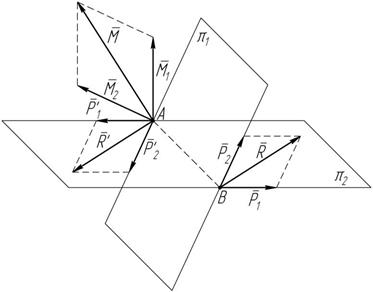 Две пары (P 1, P 1¢) и
Две пары (P 1, P 1¢) и






