
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскопараллельное движение тела
Плоскопараллельное движение (плоское) – движение, при котором все точки тела движутся в плоскостях параллельных некоторой неподвижной плоскости. Исходя из этого, движение тела можно описать движением плоской фигуры, получающейся в сечении этого тела одной из параллельных плоскостей. В свою очередь, движение фигуры в своей плоскости можно описать движением произвольного отрезка AB, принадлежащего этой фигуре. В общем случае плоское движение представляется совокупностью поступательного движения вместе с некоторым полюсом, и вращательного – поворот тела вокруг этого полюса. Таким образом, плоское движение тела определяется уравнениями: ì x A = ï í y A = f 1 (t ); f 2 (t);
(3.1)
3 в которых x A = f 1 (t) и y A = f 2 (t) – характеризуют поступательную часть движения, а j = f 3 (t) – вращательную.
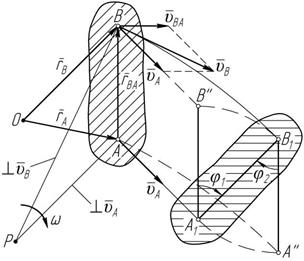
Допустим, что тело пере- местилось из положения AB в
A 1 B 1 (рисунок 3.1).
Рисунок 3.1 При этом поступательная часть движения зависит от выбора полюса, а вращательная, т.е. угол поворота (по величине и на- правлению), – не зависит (j 1 = j 2). Если за полюс взять точку A, то положение произвольной точки B определится равенством
Определим вектор скорости точки B как производную от радиус-
по времени:
dt dt dt
Вектор скорости некоторой точки B плоской фигуры равен геометрической сумме скорости полюса (точки A) и скорости этой точки (точки B) в ее вращении вместе с плоской фигурой вокруг полюса.
– вектор относительной (вращательной) скорости точки B вокруг полюса A.
u BA
всегда направлен перпендикулярно AB в сторону угловой скорости w и определяется векторным произведением:
будет равна:
= w r BA sin (w, r BA);
где l AB – длина отрезка AB, м. u BA = w l AB, (3.5)
Зачастую удобно пользоваться следующей теоремой (рисунок 3.2):
u BA всегда перпендикуля-
Рисунок 3.2 рен AB, то проецируется на эту линию (ось x) в точку. Тогда, спроецировав уравнение (3.3) на линию AB, получим: u Bx = u Ax; u A cos b = u B cos a.
В любой момент движения плоской фигуры, в ее плоскости существует точка скорость которой, в данный момент времени, равна нулю. Эта точка называется мгновенным центром скоростей (МЦС). Для определения положения МЦС необходимо восстановить перпендикуляры к векторам абсолютных скоростей точек плоской фигуры, проведенных из этих точек. На пересечении этих линий будет находиться МЦС (точка P), т.е. точка, относительно которой в данный момент времени тело совершает мгновенный поворот. Мгновенная угловая скорость тела соответственно определится:
. (3.6) AP BP Различные случаи определения положения МЦС Случай 1 (рисунок 3.3). Восстанавливаем перпендикуляры из этих точек A и B к векторам скоростей этих точек, на пересечении которых находится МЦС (точка P).
векторов u A и u B – на их пересечении будет находиться МЦС (точка P).
Случай 4 (рисунок 3.6). Если векторы скоростей точек A и B плоской фигуры равны по модулю и параллельны между собой, то МЦС находиться в бесконечности (AP =¥; BP = ¥), а мгновенная угловая скорость равна:
= u B = u A = u B = 0,
т.е. тело совершает мгновенное поступательное движение.
Теорема об ускорениях точек плоской фигуры
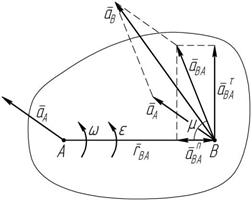
Определим ускорение произвольной точки B плоской фигуры, взяв за полюс точку A (рисунок 3.8). Для этого уравнение (3.3) представим в виде:
dt dt dt
+ dw ´ r + w ´ dr BA .
Рисунок 3.8 B A dt Так как dw = dt BA
dt dt = u BA, то:
a B = a A +
w ´ u
BA BA BA BA BA BA AB 90° – центростремительное ускорение точки B во вращении вокруг полюса A, по модулю равное:
. (3.9)
90° Тогда ускорение точки B определится уравнением:
где
t n
B A BA BA –
= l AB . (3.11) Таким образом, ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки в ее вращении вместе с плоской фигурой вокруг полюса:
a t e
BA =. (3.13)
Мгновенный центр ускорений При плоском движении тела в плоскости его движения существует точка, ускорение которой в данный момент времени равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ) Положение МЦУ можно определить, если известны: ускорение какой- либо точки тела, а также величины угловой скорости и углового ускорения этого тела.
tg m = e , w 2 вычисляют величину угла m. Далее, под углом m
точки A, в сторону углового ускорения e, откладывают отрезок AQ (рисунок 3.9), равный: Рисунок 3.9 AQ = a A . (3.14)
AQ BQ а направлены они под тем же углом m к прямым (AQ и BQ), соединяющим эти точки и МЦУ.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Относительное, переносное и абсолютное движения точки
Например, катящейся шар (из положения A в положение M) по палубе плывущего парохода (ри- Рисунок 4.1 сунок 4.1).
траекторией относительного движения, относительной скоростью u r,
a r.
a e.
абсолютного движения, абсолютной скоростью u a , абсолютным
a a. Абсолютное движение складывается из относительного и переносного:
Теорема о сложении скоростей Рассмотрим сложное движение точки M в случае, когда подвижная система отсчета связана с твердым телом, совершающим произвольное движение в пространстве (рисунок 4.2). Неподвижную систему отсчета обозначим O 1 x 1 y 1 z 1, подвижную – Oxyz.
определится:
a
dt
a dt dt
dt dr r dt
Представив r r
в виде (x r i + y r j + z r k),
= æ dx r i
+ dy r j + dz r k ö + æ di x
+ dj y
+ dk z
ö . (4.3)
÷ ç dt r dt r dt r ÷ è ø è ø В правой части уравнения (4.3) первое слагаемое представляет собой относительную скорость:
+ dy r j + dz r k ö = u
i + u
j + u
k = u . (4.4)
rx ry rz r è ø
Орты i, j, k оставаясь неизменными по модулю, вращаются вокруг
W с угловой скоростью w, поэтому производная от
и вектора соответствующего орта:
dt = w e ´ j; dt = w e ´ k. (4.5)
+ dj y
+ dk z ö = w ´ (x i
+ y j + z k)= w
´ r. (4.6)
ç dt r dt r dt r ÷
è ø
С учетом (4.4) и (4.6), производная
(4.3), будет равна:
dr r, определяемая выражением
+ w ´ r, (4.7)
– скорость точки M при ее вращении вокруг мгновенной оси W, проходящей через полюс O, в переносном
связан с неподвижной системой отсчета O 1 x 1 y 1 z 1, то
= u O
– скорость полюса O в переносном движении, м/с. Подставляя (4.7) в (4.2), получим:
a r e r dt
u a = u r + u MO + u O , (4.9) – Тогда уравнение (4.9) примет вид:
Таким образом, абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей.
u a = . (4.11)
Теорема о сложении ускорений Вектор абсолютного ускорения точки M определится:
a dt Тогда уравнение (4.8) примет вид:
dt dt dt 2
d u r dt и d (w e ´ r r ) , входящие в уравнение
i + u j + u k, производная d u r, с учетом
r (4.5), будет равна: rx ry rz dt
+ u ry j + u rz k)
dt dt
+ d u ry j + d u rz k ö + æ di u
+ dj u
+ dk u ö ; dt ç
÷ ç dt rx dt ry dt rz ÷ è ø è ø
= (a i + a j + a k)+ w ´ (u
k);
+ w ´ u
, (4.13) dt r e r
– относительное ускорение точки M. Рассмотрим производную по времени от векторного произведения
´ dr r .
r e dt
d w e =
, а производная dr r согласно (4.7) равна u + w ´ r,
dt e
dt
´ (u
r e r dt e r e r e r
´ r + w ´ u + w ´ (w ´ r). (4.14)
С учетом (4.13) и (4.14) уравнение (4.12) примет вид: d 2 r
a a = a r + w e ´ u r + e e ´ r r + w e ´ u r + w e ´ (w e ´ r r ) + e,
dt 2 или в такой последовательности
d 2 r
a a = a r + e + e e ´ r r + w e ´ (w e ´ r r ) + 2(w e ´ u r ), (4.15) dt 2
где e dt 2 = a O – ускорение полюса O в переносном движении;
– вращательное ускорение точки M во вращении вокруг мгновенной оси W, проходящей через полюс
O, в переносном движении; –
через полюс O, в переносном движении;
a r O MO MO к
O MO MO e Тогда уравнение (4.16) примет вид:
Равенство (4.17) выражает теорему Кориолиса о сложении ускорений: абсолютное ускорение точки равно геометрической сумме относительного переносного и кориолисова ускорений. Модуль абсолютного ускорения, в общем случае, определяется методом проекций. Для этого определяем алгебраические суммы проекций всех ускорений на координатные оси: a ax = a rx + a ex + a кx; a ay = a ry + a ey + a кy; a az = a rz + a ez + a кz. Тогда модуль абсолютного ускорения будет равен:
Модуль и направление вектора кориолисова ускорения
a к, стремится изменить направ-
угловой скорости w e. в направлении переносной По модулю кориолисово ускорение будет равно:
Чтобы найти направление вектора Кориолисова ускорения необходимо мысленно перенести вектор переносной угловой скорости w e в рассматриваемую точку M, а затем следовать одному из правил (рисунок 4.2).
перпендикулярен векторам w e и
кратчайший переход от w e часовой стрелки. к u r против хода
Рисунок 4.2 Правило Жуковского
руем в плоскость p перпендикулярную оси
u пр в
Кориолисово ускорение равно нулю, если: 1) w e = 0, т.е. переносное движение поступательно; 2) u r = 0, т.е. относительная скорость в данный момент времени равна нулю;
РАЗДЕЛ III. ДИНАМИКА Динамика – раздел механики, изучающий движение материальных точек (тел) в зависимости от действующих на них сил. Динамика делится на два подраздела: – динамика материальной точки; – динамика механической системы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.116.20 (0.444 с.) |
 положение
положение
 вектора r B
вектора r B
 dr B
dr B

 = dr A + dr BA;
= dr A + dr BA;
 u BA
u BA Вектор скорости
Вектор скорости

 u BA = w ´ r BA . (3.4)
u BA = w ´ r BA . (3.4) u BA = w ´ r BA
u BA = w ´ r BA
 90°
90°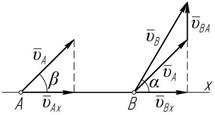 Так как вектор
Так как вектор
 w = u A = u B
w = u A = u B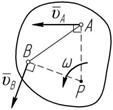 Рисунок 3.3
Рисунок 3.3
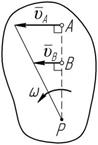 Рисунок 3.4
Рисунок 3.4
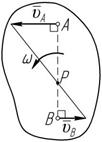 Рисунок 3.5
Рисунок 3.5
 Рисунок 3.6
Рисунок 3.6
 w = u A
w = u A



 AP BP ¥ ¥
AP BP ¥ ¥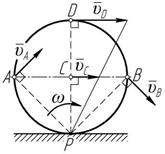 Рисунок 3.7
Рисунок 3.7
 Производная по времени от выра- жения (3.7) будет равна:
Производная по времени от выра- жения (3.7) будет равна:

 d u B = d u A + d (w ´ r BA);
d u B = d u A + d (w ´ r BA);
 и dr BA
и dr BA


 a t =
a t =  a n = w ´ u = wu sin (w, u)= wu = w 2 l
a n = w ´ u = wu sin (w, u)= wu = w 2 l BA BA BA BA BA AB
BA BA BA BA BA AB


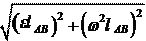
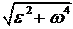 ускорение точки B в ее вращении вместе с плоской фигурой вокруг полюса A, по модулю равное:
ускорение точки B в ее вращении вместе с плоской фигурой вокруг полюса A, по модулю равное: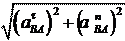 a BA = =
a BA = =

 w 2
w 2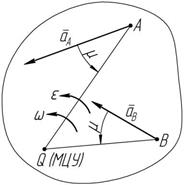 Для этого, используя формулу
Для этого, используя формулу Ускорение произвольной точки B этого тела в данный момент времени равно ее ускорению во вращательном движении вокруг МЦУ, при этом ускорения точек тела пропорциональны их расстояниям от мгновенного центра ускорений:
Ускорение произвольной точки B этого тела в данный момент времени равно ее ускорению во вращательном движении вокруг МЦУ, при этом ускорения точек тела пропорциональны их расстояниям от мгновенного центра ускорений:
 a A = a B ,
a A = a B ,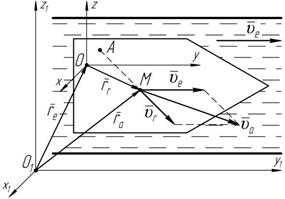 Сложным называется движе- ние, при котором точка (тело) одновременно участвует в двух или более движениях.
Сложным называется движе- ние, при котором точка (тело) одновременно участвует в двух или более движениях.
 Вектор абсолютной скорости точки M
Вектор абсолютной скорости точки M

 u = dr r
u = dr r
 получим:
получим: dr r
dr r

 dt ç
dt ç
 æ dx r i
æ dx r i мгновенной оси
мгновенной оси

 Тогда, в правой части уравнения (4.3) второе слагаемое будет равно:
Тогда, в правой части уравнения (4.3) второе слагаемое будет равно: æ di x
æ di x dt
dt dr e dt
dr e dt Модуль абсолютной скорости будет равен:
Модуль абсолютной скорости будет равен: a = d u a.
a = d u a. a a = r + + e . (4.12)
a a = r + + e . (4.12)

 dt
dt
 r = ;
r = ;



 получим:
получим:
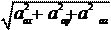
 ление вектора относительной скорости u r
ление вектора относительной скорости u r a к = 2 w e u r sin (w e , u r ).
a к = 2 w e u r sin (w e , u r ).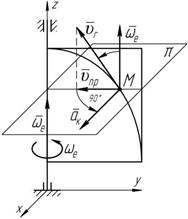 Правило векторной алгебры
Правило векторной алгебры иначе – когда вектор u r w e .
иначе – когда вектор u r w e .


