
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статически определимые и неопределимые задачи. Составные конструкции. Рычаг
Статически определимые и статически не определимые задачи
Статически определимые задачи – задачи, которые можно решать методами статики твердого тела, т.е. задачи, в которых число неизвестных не превышает числа уравнений равновесия сил (рисунок 8.1 а). Статически неопределимые задачи – задачи с числом неизвестных, превышающим число уравнений равновесия сил, т.е. задачи, для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками (рисунок 8.1 б).
Определение реакций опор составных конструкций
Рисунок 8.2 внутренние связи соответствующими реакциями, и рассматривают равновесие каждой части отдельно, а так же конструкции целиком (при необходимости).
y C ¢ = - y C соответствуют алгебраические равенства x C ¢ = x C и y C ¢ = y C , применяемые при решении задачи.
Рисунок 8.3 tg a = CK
Þ CK = 2 b tg a; x = P; y = P;
R = P.
C 2 C 2 tg a B 2sin a
× a = 0;
Рисунок 8.4 å P i x = x A - x C ¢ å P i y = y A + y C ¢ = 0; = 0. M A = - y C ¢
× a = - P × a
x A = x C ¢ = P;
y A = - y C ¢ = - P.
Проверка. Составим уравнение моментов для всей конструкции (рисунок 8.2) относительно точки C:
Подставим в полученное уравнение значения выраженных величин:
- Pa - æ - P ö a - P × b +
P sin a × 2 b = 0;
2 tg a ç 2 tg a ÷ 2sin a è ø - 2 tg a + P × a
- P × b + P × b = 0
Рычаг. Устойчивость при опрокидывании
Точка пересечения плоскости действия сил и неподвижной оси вращения рычага Рисунок 8.5 называется опорной точкой (точка O). Если рычаг находится в покое, то алгебраическая сумма моментов всех активных сил, приложенных к рычагу, относительно опорной точки равна нулю:
Рисунок 8.6 Из условия равновесия рычага определяется условие устойчивости тел при опрокидывании.
Ga - Ph = 0; Ga = Ph. Ga = M уд. – удерживающий момент; Ph = M опр. – опрокидывающий момент;
M опр.
– коэффициент устойчивости.
Найдем равнодействующую R сил P и G
(рисунок 8.7). Если линия действия силы R
1) слева от ребра A, то состояние тела устойчиво k > 1; 2) через ребро A, то состояние тела предельно
Рисунок 8.7 устойчиво k = 1; 3) справа от ребра A, то тело опрокинется k <1. ТРЕНИЕ Рисунок 9.1 Трение скольжения. Сцепление
вектору P, удерживающая тело. Эта сила называется силой трения
F тр.
При отсутствии скольжения силу трения называют силой сцепления, которая изменяется:
0 £ F
£ F max. тр тр Максимальная сила сцепления пропорциональна нормальному давлению тела:
тр fN.
где f – коэффициент трения покоя (коэффициент сцепления). Максимальная сила сцепления в широких пределах не зависит от площади трущихся поверхностей, а коэффициент сцепления зависит от характера трущихся поверхностей, а так же от их агрегатного состояния.
сцепления так как f > f ск. Угол и конус трения
– результирующий вектор от активных сил:
Так как тело под действием результирующей R a Рисунок 9.2 остается в равновесии, значит, существует сила,
и противоположно ей направленная – реакция
R ш = N + F тр.
тр тр
tg j =
max
N
= f.
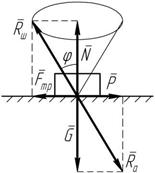
В общем случае вектор силы P можно направить как угодно в плоскости параллельной поверхности трения, поэтому вектор
R ш,
 отклоняющийся на угол j от вектора N, образует конус трения. До тех отклоняющийся на угол j от вектора N, образует конус трения. До тех
пор, пока линия действия результирующего вектора от активных сил R a будет лежать в пределах конуса трения, тело будет оставаться неподвижным.
F тр Трение качения
должен начать катиться при любой малой активной силе P. Но это идеальные условия! В действитель- ности, качение начинается при достижении силой P определенного предельного значения.
Рисунок 9.4 На рисунке 9.4 видно, что контакт цилиндра с поверхностью, по которой он катится, происходит по дуге. Поэтому, нормальная реакция N отстоит от центра цилиндра на расстоянии d, которое зависит от физических свойств поверхности. Предельное значение плеча d называется коэффициентом трения качения:
В отличие от коэффициента трения сцепления (скольжения), который является безразмерной величиной, коэффициент трения качения измеряется в единицах длины [м]. На рисунке 9.5 дана схема сил исходя из абсолютной твердости тел, но с учетом момента сопротивления качению:
Рассмотрим предельное равновесие катка, с учетом трения сцепления и трения качения: ìå P = P - F max = 0; ix тр ï
Рисунок 9.5 ïå M A (P i )= - P R + M c = 0.
Из данных уравнений видно, что скольжение начнется, если P > F max,
fN.
Качение начнется, если P > M c
или P > d N . R Но так как, обычно d << R
f, то качение начнется раньше скольжения. В связи с этим, в машиностроении энергетически выгодно заменять подшипники скольжения подшипниками качения.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.28.70 (0.058 с.) |
||||||||||||||||||||||||||||||||||
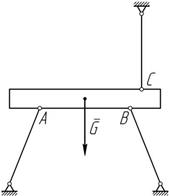 а) статически определимая задача
а) статически определимая задача
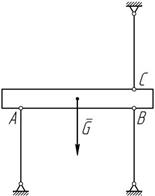 б) статически неопределимая задача
б) статически неопределимая задача
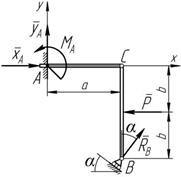 Составной называется конструкция, пред- ставляющая собой совокупность отдельных твердых тел, связанных между собой. Связи, соединяющие ее части называют внутренними (рисунок 8.2). Для рассмотрения равновесия такой конструкции ее расчленяют, заменяя
Составной называется конструкция, пред- ставляющая собой совокупность отдельных твердых тел, связанных между собой. Связи, соединяющие ее части называют внутренними (рисунок 8.2). Для рассмотрения равновесия такой конструкции ее расчленяют, заменяя
 Реакции внутренней связи шарнира C, приложенные к телам AC и CB, попарно равны по модулям и противоположны по направлениям, так как выражают действие и противодействие. Векторным равенствам
Реакции внутренней связи шарнира C, приложенные к телам AC и CB, попарно равны по модулям и противоположны по направлениям, так как выражают действие и противодействие. Векторным равенствам
 x C ¢ = - x C и
x C ¢ = - x C и Рассмотрим равновесие балки CB (рисунок 8.3):
Рассмотрим равновесие балки CB (рисунок 8.3): 2 b
2 b


 Рассмотрим равновесие балки AC (рисунок 8.4):
Рассмотрим равновесие балки AC (рисунок 8.4): å M A (P i )= M A + y C ¢
å M A (P i )= M A + y C ¢ 2 tg a;
2 tg a; 2
2 2 tg a
2 tg a P × a
P × a 2 tg a
2 tg a Þ 0 = 0.
Þ 0 = 0.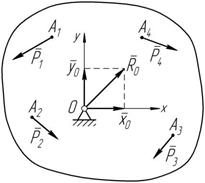 Рычаг – твердое тело, имеющее непод- вижную ось вращения, находящееся под действием сил, лежащих в плоскости, перпен- дикулярной этой оси (рисунок 8.5).
Рычаг – твердое тело, имеющее непод- вижную ось вращения, находящееся под действием сил, лежащих в плоскости, перпен- дикулярной этой оси (рисунок 8.5). å M O (P i )= 0.
å M O (P i )= 0.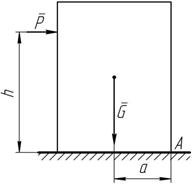
 Допустим, что к прямоугольному параллелепипеду (рисунок 8.6) весом G на высоте h приложена горизонтальная сила P, которая может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра A.
Допустим, что к прямоугольному параллелепипеду (рисунок 8.6) весом G на высоте h приложена горизонтальная сила P, которая может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра A. k = M уд.
k = M уд.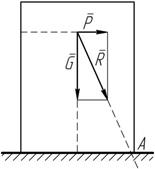 проходит:
проходит: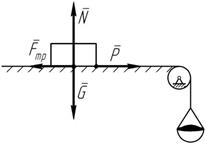 Основные законы трения носят приближенный характер. Они установлены Кулоном для сухого трения.
Основные законы трения носят приближенный характер. Они установлены Кулоном для сухого трения.
 Пусть тело, весом G, лежит на горизонтальной шероховатой поверхности (рисунок 9.1). Приложим к телу силу P. Если
Пусть тело, весом G, лежит на горизонтальной шероховатой поверхности (рисунок 9.1). Приложим к телу силу P. Если значение силы P будет незначительное, то тело будет оставаться неподвижным, т.е. в равновесии. Следовательно, появляется некая сила, до некоторого момента равная по модулю и противоположно направленная
значение силы P будет незначительное, то тело будет оставаться неподвижным, т.е. в равновесии. Следовательно, появляется некая сила, до некоторого момента равная по модулю и противоположно направленная
 Пусть на тело, находящееся в покое (рисунок 9.2), действуют активные силы: G – вес тела; P – горизонтальная сила, пытающаяся сдвинуть
Пусть на тело, находящееся в покое (рисунок 9.2), действуют активные силы: G – вес тела; P – горизонтальная сила, пытающаяся сдвинуть


 Рисунок 9.3
Рисунок 9.3
 d = d max.
d = d max. M c = d N.
M c = d N. R
R


