
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип д’аламбера (принцип кинетостатики)⇐ ПредыдущаяСтр 12 из 12
P a (рисунок 8.1),
ma = P a + N. (8.1)
– сила инерции, равная по модулю произведению массы точки на ее ускорение (Ф = ma) и направленная в сторону, противоположную ускорению. Тогда получим принцип д’Аламбера для несвободной материальной точки:
В любой момент движения материальной точки, действующие на нее, активная сила и реакция связи уравновешиваются условно приложенной силой инерции. Для механической системы При движении механической системы геометрическая сумма активных сил, реакций и условно приложенных сил инерций равна нулю:
где å P a i i i –
– геометрическая сумма условно приложенных сил инерций, Н. Принцип д’Аламбера – это условный, формальный прием, позволяющий рассматривать задачи динамики методами статики.
Рисунок 8.2
Ф = ma.
При вращательном движении (рисунок 8.2 б), относительно оси проходящей через центр масс тела, прикладывается только момент сил инерций M Ф, направленный противоположно e и равный произведению момента инерции тела ускорение e тела: J O, относительно оси O его вращения, на угловое
При плоскопараллельном движении (рисунок 8.2 в) прикладываются сила инерции (к центру масс тела) и момент сил инерций, направленные противоположно ускорениям и равные: Ф = ma C;
где a C – ускорение центра масс тела, м/с2; J C – момент инерции тела относительно центральной оси, перпендикулярной плоскости движения тела, кг × м2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ (ПРИНЦИП ЛАГРАНЖА) В общем случае на систему могут быть наложены внешние и внутренние связи. На практике эти связи реализуются в виде шарниров, нитей, стержней, поверхностей, направляющих и т.д., но их можно представить в виде геометрических линий, математических поверхностей, плоскостей, которые описываются уравнениями или неравенствами.
Классификация связей 1. Стационарные связи Связи, которые не меняются с течением времени, называются стационарными. Уравнения этих связей не зависят явным образом от времени.
Рисунок 9.1
составить систему уравнений: Пример. Кривошипно-шатунный механизм (рисунок 9.1).
A, B), для этого необходимо
x 1 = y 1 = y 3 = 0;
(x - x )2 + y 2 - l 2 = 0 . 3 2 2
В эти уравнения явно не входит параметр t, поэтому этот вид связи можно считать стационарным. 2. Удерживающие связи
Положение точки A (рисунок 9.2) при данном Рисунок 9.2 виде связи определится неравенством:
т.е. данная связь является неудерживающей.
3. Идеальные связи Связи без трения (см. раздел I, тема 1, пункт 1.3).
4. Голономные и неголономные связи Голономными называются связи, которые накладывают ограничение только на перемещение точек механической системы. В уравнения этих связей входят только координаты точек системы и не входят производные от них (проекции скоростей). Неголономными называются связи, которые накладывают ограничения на скорости точек механической системы. В уравнения неголономных связей помимо координат точек системы входят их скорости.
Возможные перемещения. Принцип Лагранжа
совпадает с приращением дуговой координаты d s (см. раздел II, тема 1, пункт 1.3 – скорость точки). Понятие возможного перемещения точки или механической системы есть понятие чисто геометрическое и не зависит от действующих на точку или систему сил, а зависит только от характера наложенных связей. Действительное перемещение это одно из возможных перемещений. Перемещение, при котором точка или система покидает наложенные связи, не является «возможным».
Для равновесия механической системы с идеальными связями необходимо и достаточно чтобы сумма элементарных работ активных сил на возможных перемещениях механической системы равнялась нулю:
Возможные перемещения (виртуальные, бесконечно малые) – то, что можно совершить не нарушая связи.
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ (ПРИНЦИП Д’АЛАМБЕРА- ЛАГРАНЖА) При движении механической системы сумма элементарных работ активных сил и условно приложенных сил инерций на возможных перемещениях механической системы равна нулю:
ЛИТЕРАТУРА 1. Бать, М.И. Теоретическая механика в примерах и задачах. В 2-х т. Т. 1. Статика и кинематика: учеб. пособие / М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. – 11-е изд., стер. – СПб.: Лань, 2010. – 672 с. 2. Бать, М.И. Теоретическая механика в примерах и задачах. В 2-х т. Т. 2. Динамика: учеб. пособие / М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. – 9-е изд., стер. – СПб.: Лань, 2010. – 640 с. 3. Бутенин, Н.В. Курс теоретической механики Т. 1. Статика и кинематика. Т. 2. Динамика / Н.В. Бутенин, Я.Л. Лунц, Д.Р Меркин. – 11-е изд., стер. – СПб.: Лань, 2009. – 736 с. 4. Бухгольц, Н.Н. Основной курс теоретической механики / Н.Н. Бухгольц. В 2-х ч. Ч. 2. Динамика системы материальных точек: учеб. пособие. – 7-е изд., стер. – СПб.: Лань, 2009. – 336 с. 5. Бухгольц, Н.Н. Основной курс теоретической механики. / Н.Н. Бухгольц. В 2-х ч. Ч. 1. Кинематика, статика, динамика материальной точки: учеб. пособие. – 10-е изд., стер. – СПб.: Лань, 2009. – 480 с. 6. Лачуга Ю.Ф. Теоретическая механика / Ю.Ф. Лачуга, В.А. Ксендзов. – 2-е изд., перераб. и доп. – М.: Колос, 2005. – 576 с. 7. Никитин, Н.Н. Курс теоретической механики: учебник / Н.Н. Никитин. – 8-е изд., стер. – СПб.: Лань, 2010. – 720 с. 8. Тарг, С.М. Краткий курс теоретической механики / С.М. Тарг. – 20-е изд., стер. – М.: Высш. шк., 2010. – 416 с. 9. Яблонский, А.А. Курс теоретической механики. Ч. I Статика. Кинематика. Ч. II Динамика / А.А. Яблонский, В.М. Никифорова. – 15- е изд., стер. – М.: КноРус, 2010. – 608 с.
Учебное издание
Букаткин Рустем Николаевич, Корнеев Дмитрий Витальевич
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.120 (0.031 с.) |
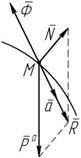 Пусть несвободная материальная точка M массой m
Пусть несвободная материальная точка M массой m движется под действием активной силы тогда:
движется под действием активной силы тогда:





 å P a + å N + å Ф = 0, (8.3)
å P a + å N + å Ф = 0, (8.3) å N i – геометрическая сумма реактивных сил (реакций связей), возникающих от действия активных сил, Н;
å N i – геометрическая сумма реактивных сил (реакций связей), возникающих от действия активных сил, Н; å Ф i
å Ф i
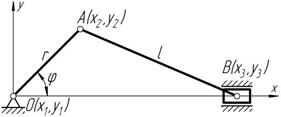 Для определения произвольного положения КШМ необходимо определить положения трех точек (O,
Для определения произвольного положения КШМ необходимо определить положения трех точек (O,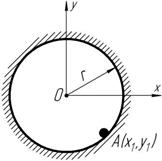 Удерживающая связь – это связь, при которой в любой момент движения точка остается на поверхности связи. Уравнения удерживающих связей определяется равенствами, а неудержи- вающих связей – неравенствами.
Удерживающая связь – это связь, при которой в любой момент движения точка остается на поверхности связи. Уравнения удерживающих связей определяется равенствами, а неудержи- вающих связей – неравенствами.


