
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении кинетической энергии
Рисунок 7.1 Работа и мощность сил Если тело движется поступательно прямоли- нейно, а сила, приложенная к нему, постоянна по модулю и направлению (рисунок 7.1), то работа силы определится скалярным произведением
или по модулю A = P × D r × cos(P, D r).
Так как D r = s, то
Если 0 £ a < 90°, то работа положительна. Если a = 90°, то работа равна нулю. Если 90° < a £180°, то работа отрицательна.
Рисунок 7.2 Тогда элементарная работа d A определится:
силы P
где ds – приращение дуговой координаты (алгебраическая величина).
Разложим силу P на составляющие (проекции на естественные оси):
d A = P t ds. (7.1) Уравнение (7.1) показывает, что работу на элементарном участке ds
совершает только касательная составляющая P t силы P; работа
нормальной составляющей
P n, перпендикулярной направлению вектора скорости u точки M, равна нулю. Представим элементарную работу силы как скалярное произведение:
Тогда в проекции на декартовы оси координат получим: d A = P x dx + P y dy + P z dz.
Полная работа силы на каком-либо конечном перемещении AB равна:
A = ò d A = ò(P x d x + P y d y + P z d z). (7.2) A A Рисунок 7.3 Работа силы тяжести
Воспользуемся выражением (7.2). Для этого определим проекции силы
G на декартовы оси координат:
G x = 0; G y = 0; G z = - G.
z 2 z 2
A = ò (- G) d z = - G ò d z = - G (z 2 - z 1 ) = G (z 1 - z 2 ), z 1 z 1 где z 1 - z 2 = h – величина вертикального перемещения точки M, м. Таким образом, работа силы тяжести определяется выражением: A = ± Gh. Знак «+» соответствует перемещению материальной точки вниз, а знак «» – перемещению материальной точки вверх.
Работа силы тяжести не зависит от вида траектории, по которой движется точка ее приложения, а зависит лишь от расстояния между горизонтальными плоскостями, проходящими через начальное и конечное положения точки приложения силы. Работа силы упругости
При растяжении пружины будет возникать сила, стремящаяся вернуть ее в положение равновесия – сила упругости, модуль которой пропорционален удлинению пружины и равен P упр = cx, где x – величина удлинения пружины, м.
Рисунок 7.4 Определим проекции силы
P упр на декартовы оси координат: P упр (x) = - cx; P упр (y) = 0; P упр (z) = 0. Тогда работа силы
P упр при удлинении пружины на l будет равна:
l l A = (- cx) dx = A = - c xdx = - c (l 2 - l 2 )= c
(l 2 - l 2), ò ò 2 0 2 0 l 0 l 0 где l 0 и l – соответственно начальное и конечное удлинения пружины, м.
Работа силы при вращательном движении тела
d A e = P e ds.
Так как i i t ds i = h i d j, то
i
Рисунок 7.5 При действии нескольких сил:
e – главный момент внешних сил относительно оси z, Н× м.
M j = 0, тогда полная работа на
M e = const, то A = ò j 0
M e d j. A = M e j 0 d j = M e (j - j ).
Мощность силы – работа, совершаемая силой в единицу времени. Средняя мощность определяется выражением:
[ N ] = é Дж ù = [Вт]. ëê c úû Истинная мощность в данный момент времени определится по формуле: N = d A . dt
= P × dr = P × u = P u cos(P, u).
M e d j e N = z = M z w. dt Теорема об изменении кинетической энергии Пусть материальная точка массой m движется под действием сил
P 1,
P 2, …,
P n. Согласной второму закону динамики:
Спроецируем уравнение (7.3) на касательную ось и умножим обе его части на приращение дуговой координаты ds: m a t d s = å P i t d s. (7.4) Рассмотрим левую часть уравнения (7.4): d u ds æ u 2 ö æ m u 2 ö
Согласно (7.1) è ø è ø å P i t d s = å d A i , тогда уравнение (7.4) примет вид: æ m u 2 ö
где
m u 2
è ø
– кинетическая энергия материальной точки, Дж. Проинтегрировав выражение (7.5) получим теорему об изменении кинетической энергии материальной точки в интегральном виде:
= å A i . (7.6) 2 2 Изменение кинетической энергии материальной точки на некотором перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении. Для механической системы Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на механическую систему на том же перемещении: T - T 0 = å A e + å A j, (7.7)
T 0 и T – соответственно кинетические энергии механической системы в ее начальном и конечном положениях, Дж;
– сумма работ внешних сил, приложенных к механической системе, на ее перемещение из начального положения в конечное, Дж; – сумма работ внутренних сил механической системы на том же перемещении, Дж.
Вычисление кинетической энергии твердого тела при различных видах движения
При поступательном движении:
m u 2
При вращательном движении: T = .
J w 2 T = z . 2 При плоскопараллельном движении: = m u 2 + J w 2
T С С . 2 2 Где J – момент инерции тела относительно оси его вращения, кг × м2;
J С – момент инерции тела относительно центральной оси, перпен- дикулярной плоскости движения тела, кг × м2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.252.8 (0.085 с.) |
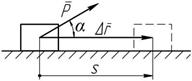



 A = P × D r
A = P × D r
 A = Ps cos a, [ A ]= [Н × м]= [Дж].
A = Ps cos a, [ A ]= [Н × м]= [Дж].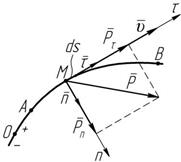 Если движение криволинейно, а сила изме- няется по величине и направлению (рисунок 7.2), то траекторию движения следует разбить на бесконечно малые элементарные участки ds.
Если движение криволинейно, а сила изме- няется по величине и направлению (рисунок 7.2), то траекторию движения следует разбить на бесконечно малые элементарные участки ds. d A = P d s cos(P, t),
d A = P d s cos(P, t),



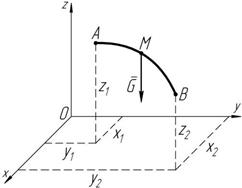 Определим работу силы тяжести G, действующей на материальную точку M, на перемещении AB, величина которого мала по сравнению с радиусом Земли (рисунок 7.3). В этом случае модуль и направление силы тяжести постоянны.
Определим работу силы тяжести G, действующей на материальную точку M, на перемещении AB, величина которого мала по сравнению с радиусом Земли (рисунок 7.3). В этом случае модуль и направление силы тяжести постоянны.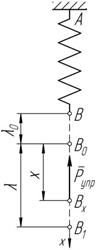 Рассмотрим пружину AB, конец A которой закреплен неподвижно (рисунок 7.4).
Рассмотрим пружину AB, конец A которой закреплен неподвижно (рисунок 7.4).
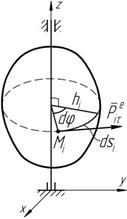 Согласно уравнению (7.1), элементарная работа внешней силы, приложенной к i -й точке тела вращаю- щегося вокруг вертикальной оси z (рисунок 7.5), определится:
Согласно уравнению (7.1), элементарная работа внешней силы, приложенной к i -й точке тела вращаю- щегося вокруг вертикальной оси z (рисунок 7.5), определится:






 ma t ds = m dt ds = m dt d u = m u d u = md ç 2 ÷ = d ç 2 ÷ .
ma t ds = m dt ds = m dt d u = m u d u = md ç 2 ÷ = d ç 2 ÷ .
 2
2






