
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синергетика. Принципы самоорганизации различных сложных системСодержание книги
Поиск на нашем сайте
Элементы неравновесной термодинамики. Классическую термодинамику с большим основанием можно было бы назвать термостатикой, поскольку она дает полное количественное описание только равновесных (обратимых) процессов. Для неравновесных процессов она указывает лишь на направление их эволюции с помощью закона возрастания энтропии. Термодинамика, созданная для объяснения неравновесных процессов (диффузии, теплопроводности и др.), называется линейной неравновесной термодинамикой. В этой теории отклонения системы от равновесия считаются малыми, а уравнения, положенные в ее основу, являются линейными. В неравновесных системах температура Такие процессы называются явлениями переноса. Простейшими примерами явлений переноса могут служить теплопроводность и диффузия. Процесс теплопередачи из областей системы с более высокой температурой в области с меньшей температурой, вследствие хаотического движения молекул, называется теплопроводностью. Процесс переноса вещества из областей системы с более высокой концентрацией в области с меньшей концентрацией в результате хаотического движения молекул, называется диффузией. Движущей силой любого явления переноса служит градиент соответствующей величины, который называется обобщенной термодинамической силой
и
где Не вдаваясь в подробности, укажем лишь то, что нестационарные процессы переноса сопровождаются перекрестными потоками. Например, градиент температуры, кроме потока теплоты, вызывает поток вещества (термодиффузия). И, наоборот, градиент концентрации, кроме потока вещества, создает потоки теплоты. Взаимосвязь потоков и обобщенных сил выражается линейными уравнениями Онсагера
где Согласно Онсагеру кинетические коэффициенты для перекрестных потоков равны В 1947 году бельгийский физик русского происхождения И. Пригожин, исходя из соотношений Онсагера, доказал важную теорему термодинамики неравновесных процессов. По этой теореме стационарному (
где Для равновесного состояния Устойчивость стационарных состояний с минимальным производством энтропии обусловлена принципом Ле-Шателье–Брауна. Согласно этому принципу в системе, выведенной из равновесного состояния внешним возмущением, возникают процессы, направленные на ослабление этого возмущения. Одним из проявлений этого принципа является правило Ленца из электродинамики. Открытые системы. В открытых системах происходит обмен энергией и веществом с окружающей средой. В этом случае изменение энтропии может быть представлено в виде суммы
Величина В природе имеет место два типа упорядоченности – статическая и динамическая. В первом случае упорядоченность возникает в результате фазового перехода системы в состояние равновесия. Примером статической упорядоченности может служить превращение воды в лед. Динамическая упорядоченность связана не с уменьшением энтропии при понижении температуры, а с ее оттоком из открытой системы в окружающую среду. В этом их принципиальное отличие.
В настоящее время, кроме живых организмов, известно множество примеров самоорганизации в открытых системах неорганической природы. При этом возникают упорядоченные структуры, которые бывают пространственными или временными. Структуры, Диссипативная система (лат. dissipatio – рассеяние) – это открытая система, в которой приток энергии (вещества) сопровождается ее оттоком (рассеянием) в окружающую среду. Приток энергии (вещества) должен компенсировать потери и обеспечивать существование упорядоченных структур. Диссипативные структуры возникают при выполнении следующих условий. 1. Система должна быть открытой и макроскопической, т.е. состоящей из огромного числа атомов, молекул и т.д. Упорядоченное состояние в таких системах всегда имеет кооперативный (коллективный) характер. 2. Наличие в системе отрицательного потока энтропии. 3. Система находится в состоянии вдали от равновесия. 4. Нелинейность уравнений, описывающих систему. 5. Выполнение универсального критерия эволюции системы Пригожина–Гленсдорфа ( Диссипативные структуры являются устойчивыми образованиями. Однако их существование обеспечивается устойчивым поступлением энергии и вещества в систему. При их прекращении структура разрушается, поэтому такие структуры иногда называют «летучими». Рассмотрим несколько примеров самоорганизации. Ячейки Бенара. Они напоминают пчелиные соты (рисунок 87) и были обнаружены еще в 1901 году Х. Бенаром. Ячейки Бенара возникают в плоском слое первоначально однородной вязкой жидкости, равномерно подогреваемой снизу. Для их наблюдения обычно используют налитое в плоский сосуд (сковороду) минеральное масло, смешанное с мелкодисперсным алюминиевым порошком. При нагревании слоя жидкости снизу между нижней и верхней поверхностями возникает постоянный градиент температуры. Пусть 1 Весь слой жидкости распадается на одинаковые вертикальные шестигранные призмы (рисунок 87б). В центральной области призмы жидкость поднимается, а по граням призмы – опускается.
Образование ячеек Бенара сопровождается уменьшением энтропии системы. Система, обмениваясь с окружающей средой теплотой и находясь в стационарных условиях (при
т.е. самоорганизация системы поддерживается за счет поглощения отрицательной энтропии (негэнтропии). Элементарное объяснение причин возникновения ячеек Бенара заключается в следующем. Вследствие теплового расширения жидкости возникает инверсный градиент плотности, направленный противоположно силе тяжести. Жидкость у нижней поверхности имеет меньшую плотность, чем вблизи верхней (
Рисунок 89
Самой удивительной чертой структурирования жидкости является скачкообразный переход от простого хаотического движения молекул к их сложному самосогласованному (когерентному) упорядоченному движению. Воспроизведение ячеистой структуры наблюдается при одном и том же значении критического параметра Эволюцию системы из критического неустойчивого состояния определяют флуктуации. Они решают, каким будет вращение жидкости в данной ячейке – право- или лево-вращательным. Причем этот процесс носит неуправляемый, чисто случайный характер. Как только выбор сделан, поведение системы становится строго детерминированным: установившиеся направления в ячейках в дальнейшем сохраняются. В рассмотренном примере наглядно просматривается организующая роль как статистических, так и динамических закономерностей при переходе системы из хаоса в упорядоченное состояние. Аналогичный дуализм имеет место и в живой материи, где эволюция видов опреде-ляется как мутациями, имеющими случайный характер, так и естественным отбором – динамическим фактором. Примером самоорганизации в химии является реакция Белоусова–Жаботинского. Реакция Белоусова–Жаботинского происходит в интенсивно перемешиваемой реакционной смеси, состоящей из сульфата церия Ce2(SO4), малоновой кислоты CH2(COOH)2 и бромата калия KBrO3, растворенного в серной кислоте. Добавление ферроина позволяет следить за ходом реакции по изменению цвета смеси. При концентрации реагирующих веществ, превышающих некоторые критические значения, цвет раствора со временем периодически изменяется от красного (при избытке Ce3+) до синего (при избытке Ce4+) (рисунок 90). Такой эффект получил название – химические часы.
Рисунок 90
Еще одним примером самоорганизующей системы является лазер. При самом грубом описании лазер – это стеклянная трубка, в которой находится активная среда. Свет в трубку поступает от некогерентного источника (лампы), а выходит из нее узконаправленный когерентный световой пучок (рисунок 91).
Рисунок 91
При малой мощности накачки испускаемые лазером электромагнитные волны некоррелированы и излучение подобно излучению обычной лампы. Такое некогерентное излучение – это шум, хаос. При повышении мощности накачки до порогового критического значения некогерентное электромагнитное излучение лампы накачки преобразуется в когерентное излучение лазера. При этом излучение отдельных атомов активного вещества оказывается строго коррелированным, т.е. самоорганизованным. Биологические системы. Живая материя представляет пример образования множества высокоорганизованных структур. Живой организм – это открытая система, которая непрерывно получает потоки энергии и веществ и выделяет в окружающую среду отходы жизнедеятельности. В биологической системе процессы самоорганизации позволяют преобразовать энергию с молекулярного хаотического уровня на упорядоченный макроскопический уровень (например, при мышечном сокращении). До полного объяснения функционирования биологических систем на основе представления синергетики еще очень далеко. Однако можно привести ряд примеров, где понятия и математический аппарат синергетики дает удовлетворительный качественный результат. Таким примером является система «жертва-хищник». Пусть система состоит из двух видов – это «жертва» и «хищник» (например, кролики и лисицы). Рассмотри динамику популяций этой системы. Кролики ( В местах обитания кроликов появились лисицы, для которых кролики являются добычей. Поскольку изначально кроликов было много, то за счет их поедания возрастает число лисиц. В свою очередь лисицы сами являются жертвами – например, человека, что непосредственно не отражается на динамике популяций. Однако этим подчеркивается аналогия жертв человека–лисиц с теплотой, выводимой из системы при образовании ячеек Бенара. Совершенно очевидно, что в действительности происходят периодические колебания численности популяции кроликов и лисиц. Причем за увеличением численности кроликов следует увеличение численности лисиц. Уменьшение численности кроликов сопровождается столь же резким снижением численности лисиц. Затем этот процесс повторяется и образуются так называемые популяционные волны, изображенные на рисунке 92.
Рисунок 92
Процессы, подобные рассмотренным, наблюдаются и в социальных системах. Основными элементами общества являются люди, их связи и поведение. Как целое общество образует новое качество, которое не сводится к сумме качеств ее элементов, а возникает в результате их взаимодействия. Конечно, аналогия процессов самоорганиза-ции в обществе с выше рассмотренными весьма условна. Нельзя сравнивать человека с молекулой. Тем не менее понятийный и математический аппарат нелинейной термодинамики и синергетики довольно успешно применяется при описании различных процессов самоорганизации в человеческом обществе (например, в экономике). Теория бифуркаций. Все рассмотренные выше примеры самоорганизации можно рассмотреть с общих позиций. Особая роль в эволюции сильно неравновесной системы отводится нелинейности и внешним возмущениям. Рассмотрим произвольную систему (изолированную или открытую), эволюционирующую в соответствии с определенными динамическими законами. Пусть в силу каких-либо причин система оказалась в состоянии Однако состояние реальных систем никогда не остается постоянным, что обусловлено неконтролируемым взаимодействием системы с окружающей средой. Влияние внешней среды на внутреннюю динамику системы отражается в том, что мгновенное состояние
где В макроскопических системах, состоящих из очень большого числа частиц, существуют возмущения, не связанные с внешней средой. Эти возмущения обусловлены внутренней динамикой системы, и называются флуктуациями. Флуктуации представляют собой случайные отклонения системы из состояния равновесия. Например, в некотором малом объеме макроскопической системы скорости частиц могут быть несколько большими, чем в соседнем. В другом малом объеме число частиц (плотность) может быть повышена или понижена и т.д. Таким образом, переменные состояния системы Если состояние системы Например, аттракторами являются состояние термодинамического равновесия в изолированных системах, ячейки Бенара и колебания концентраций ионов Установив принципиальные причины, по которым состояние системы может непрерывно отклоняться от стандартного состояния Наиболее общие принципы эволюции диссипативных систем можно выяснить из анализа решений нелинейного уравнения с единственным управляющим параметром
Этому уравнению соответствуют три решения для стационарного состояния ( Термин «бифуркация» означает развилка или разделение надвое (от лат. bi – «два» и furca – «развилка». При малых значениях
усиливаются из-за нелинейности системы. Система все дальше и дальше уходит от Дальнейшею эволюцию системы из точки будет решать случайная флуктуация в точке бифуркации. Общий вывод заключается в том, что переход хаоса в упорядоченное состояние связан с появлением новых ветвей решений уравнения для При дальнейшем увеличении движущих сил (например, градиента температуры в опыте Бенара) возникают новые ветвления – каскад бифуркаций (рисунок 94).
Система, эволюционируя с множественными бифуркациями, достигает такой степени сложности и запутанности, что сложность становится уже беспорядком. Такое состояние принято называть динамическим хаосом. Если эволюция диссипативной системы во времени характеризуется теорией бифуркации, то описанием устойчивости структур в окрестности точки бифуркации занимается теория катастроф. В теории катастроф изучают явления, которые могут возникнуть в ответ на плавное изменение внешних условий. Эта теория создавалась в 70-х годах ХХ в. и сразу получила многочисленные приложения к объектам различной природы. Исследования биения сердца, моделирование деятельности мозга, моделирование динамики землетрясений, прочности конструкций – вот далеко не полный перечень объектов исследования теории катастроф. Теория катастроф позволяет свести все многообразие сложных ситуаций к небольшому числу точно изученных схем. Сложные системы, состоящие из многих взаимодействующих элементов, постоянно самоорганизуются. И вместе с тем достигают некоторого критического состояния, в котором даже незначительные события вызывают цепную реакцию, приводящую к катастрофе. Иными словами, малые причины вызывают большие следствия или «эффект бабочки», когда возмущения, вызванные полетом бабочки, приводят к образованию тайфунов, торнадо и т.д. Чтобы наглядно представить эффект самоорганизованной критичности, обратимся к компьютерному моделированию Г. Хелда. Он разработал устройство, которое медленно и равномерно – по одной песчинке – насыпало песок на круглую подложку. Песчинки вначале остаются в месте падения, потом громоздятся в кучу. Когда склон становится очень крутым, достигается критическое состояние, в котором куча теряет устойчивость, и одна песчинка вызывает катастрофу – песчинка образует лавину. Бифуркационные процессы имеют место и в социальных системах. Если общество достигает порога устойчивости (точки бифуркации), то оно вступает в состояние хаоса. Однако динамический хаос не приводит к полной неупорядоченности. Он может служить переходным процессом от одного менее упорядоченного состояния в более упорядоченное состояние. Эволюция социальных экономических и политических систем имеет сложный характер, которая при определенных условиях теряет устойчивость и устремляется к точке бифуркации (революция или социальная катастрофа). После революции она выходит на новый режим устойчивого развития, который может эволюционировать в новую бифуркацию (революцию). В современном мировом сообществе имеется множество примеров такого развития общественных систем. Не является исключением и Россия, в истории которой за последние два века произошло несколько революций.
Выводы 1. Основу физики макроскопических систем составляют две большие группы теорий – динамические и статистические. В динамических теориях процессы и явления подчиняются однозначным закономерностям. В основу статистических теорий положены вероятностные (статистические) закономерности. Поведение макроскопических систем является предметом изучения термодинамики и статистической физики. Макроскопическая система – это тело или совокупность тел, состоящих из атомов или молекул. 2. Статистический метод основан на молекулярно-кинетических представлениях, согласно которым атомы и молекулы, из которых состоят тела, находятся в непрерывном хаотическом движении. 3. Термодинамика – наука феноменологическая. Это означает, что в ее основе лежат несколько фундаментальных принципов (начал), которые являются обобщением многочисленных экспериментальных фактов. Термодинамика – наука динамическая, она изучает макроскопические свойства тел, не интересуясь их микроскопической структурой. В основу термодинамики положены три начала. Первое начало выражает закон сохранения и превращения энергии в макроскопических системах: энергия не создается из ничего и не исчезает бесследно, а только превращается из одного вида в другой. Второе начало термодинамики имеет несколько эквивалентных формулировок, но наиболее общей из них является закон возрастания энтропии в замкнутых системах, который включает все остальные формулировки. Введенная Клаузиусом функция состояния – энтропия определяет 4. Энтропия связана с информацией. Эта связь положена в основу количественной теории информации, созданной Шенноном на основе формулы Больцмана для энтропии. Количество информации и энтропия различаются только знаками, поэтому количество информации часто называют негэнтропией. Росту энтропии системы всегда соответствует убыль информации и наоборот. 5. В открытых системах происходит обмен энергией, веществом и информацией с окружающей средой. В этом случае энтропия может как возрастать, так и убывать. При уменьшении энтропии в открытой системе возможны процессы самоорганизации и система переходит из хаоса в упорядоченное состояние. Таким образом, разрешается фундаментальное противоречие, связанное с образованием в природе многочисленных упорядоченных структур (от устройства Вселенной до строения клетки). Структуры, возникающие в открытых неравновесных нелинейных системах, называются диссипативными, поскольку приток энергии сопровождается ее оттоком в окружающую среду. Примерами диссипативных структур являются: ячейки Бенара, реакция Белоусова–Жаботинского (химические часы), лазеры, популяционные волны и другие. 6. Согласно третьему началу термодинамики (теоремы Нернста) энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к абсолют-ному нулю. Из третьего начала следует, что кристалл с идеальной кристаллической ре-шеткой при абсолютном нуле является примером предельной упорядоченности – его энтропия равна нулю. Наиболее беспорядочному, хаотизированному состоянию свойст-венна наибольшая энтропия.
Контрольные вопросы 1. В чем различие между количеством теплоты и внутренней энергией? 2. Сформулируйте закон сохранения и превращения энергии. 3. Приведите математическое определение энтропии. 4. Раскройте содержание гипотезы «тепловой смерти» Вселенной. 5. В чем заключается статистический смысл энтропии? 6. При каких условиях возможны процессы самоорганизации в открытых системах? 7. Приведите примеры образования диссипативных структур.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.27.69 (0.014 с.) |

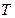 , концентрация (
, концентрация (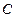 ) и другие параметры принимают различные значения в различных частях системы. Возникновение градиентов температуры, концентрации, потенциала сопровождается потоками теплоты, массы и заряда.
) и другие параметры принимают различные значения в различных частях системы. Возникновение градиентов температуры, концентрации, потенциала сопровождается потоками теплоты, массы и заряда.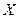 . В явлениях теплопроводности и диффузии такими обобщенными силами являются градиент температуры (grad
. В явлениях теплопроводности и диффузии такими обобщенными силами являются градиент температуры (grad 
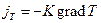 ,
,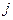 – плотность потоков вещества и теплоты соответственно;
– плотность потоков вещества и теплоты соответственно; 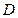 – коэффициент диффузии;
– коэффициент диффузии; 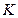 – коэффициент теплопроводности.
– коэффициент теплопроводности.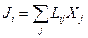 (j =1, 2, 3,…),
(j =1, 2, 3,…),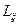 – кинетические коэффициенты (
– кинетические коэффициенты (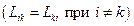 .
.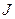 – не зависят от времени) состоянию системы соответствует минимальное производство энтропии (
– не зависят от времени) состоянию системы соответствует минимальное производство энтропии (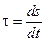 ). В общем случае
). В общем случае 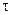 выражается соотношением
выражается соотношением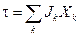 ,
,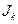 – термодинамические потоки вещества или энергии являются факторами необратимости, создающие энтропию; величины
– термодинамические потоки вещества или энергии являются факторами необратимости, создающие энтропию; величины 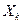 характеризуют физические факторы, действием которых создаются и поддерживающие термодинамические потоки.
характеризуют физические факторы, действием которых создаются и поддерживающие термодинамические потоки.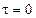 .
.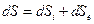 .
.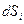 связана с производством энтропии, обусловленного необратимостью происходящих в системе процессов (
связана с производством энтропии, обусловленного необратимостью происходящих в системе процессов (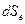 обусловлено обменом энергией и веществом с окружающей средой. Оно может быть как положительным, так и отрицательным, в зависимости от того, получает или отдает система теплоту. Поэтому знак полного изменения энтропии (
обусловлено обменом энергией и веществом с окружающей средой. Оно может быть как положительным, так и отрицательным, в зависимости от того, получает или отдает система теплоту. Поэтому знак полного изменения энтропии (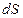 ) в открытой системе определяется знаком и величиной
) в открытой системе определяется знаком и величиной 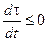 ).
).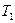 – температура жидкости у дна, а
– температура жидкости у дна, а 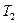 – на поверхности (
– на поверхности (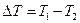 невелика (
невелика (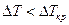 ), жидкость с частичками порошка неподвижна, а передача теплоты происходит лишь путем теплопроводности. В этом случае справедливо линейное приближение, описываемое уравнением Фурье. При достижении
), жидкость с частичками порошка неподвижна, а передача теплоты происходит лишь путем теплопроводности. В этом случае справедливо линейное приближение, описываемое уравнением Фурье. При достижении 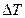 некоторого критического значения (
некоторого критического значения (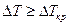 ) объем жидкости внезапно приходит в движение и возникают конвекционные потоки, которые резко усиливают теплообмен (рисунок 88). Описание системы становится нелинейным.
) объем жидкости внезапно приходит в движение и возникают конвекционные потоки, которые резко усиливают теплообмен (рисунок 88). Описание системы становится нелинейным. а) б)
а) б)

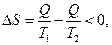
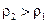 ). Если выделенный элементарный объем (
). Если выделенный элементарный объем (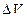 ) в нижней части слоя жидкости, вследствие возмущения немного смещается вверх, то он попадает в область повышенной плотности. Сила Архимеда станет больше силы тяжести, и возникает восходящий поток жидкости. В верхней части малый объем, смещаясь вниз, попадает в область пониженной плотности, и архимедова сила будет меньше силы тяжести, возникает нисходящее движение жидкости (рисунок 89).
) в нижней части слоя жидкости, вследствие возмущения немного смещается вверх, то он попадает в область повышенной плотности. Сила Архимеда станет больше силы тяжести, и возникает восходящий поток жидкости. В верхней части малый объем, смещаясь вниз, попадает в область пониженной плотности, и архимедова сила будет меньше силы тяжести, возникает нисходящее движение жидкости (рисунок 89).
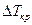 . Причем в различных опытах жидкость в соседних ячейках приходит во вращение либо по часовой стрелке (
. Причем в различных опытах жидкость в соседних ячейках приходит во вращение либо по часовой стрелке (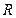 ), либо против часовой стрелки (
), либо против часовой стрелки (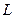 ).
).

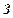 ) поедают траву (
) поедают траву (
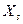 , в котором она будет находиться и впоследствии. В случае изолированной системы это состояние равновесия. В диссипативной системе оно может быть либо состоянием термодинамического равновесия, либо стационарным неравновесным состоянием.
, в котором она будет находиться и впоследствии. В случае изолированной системы это состояние равновесия. В диссипативной системе оно может быть либо состоянием термодинамического равновесия, либо стационарным неравновесным состоянием.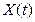 системы не совпадает со стационарным состоянием
системы не совпадает со стационарным состоянием 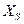 . Состояние системы будет характеризоваться некоторым обобщенным усредненным параметром
. Состояние системы будет характеризоваться некоторым обобщенным усредненным параметром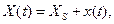 (84)
(84)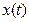 называется возмущением (не путать его с контролируемыми внешними возмущениями, специально созданными в условиях эксперимента).
называется возмущением (не путать его с контролируемыми внешними возмущениями, специально созданными в условиях эксперимента). устойчиво, и оно называется аттрактором (англ. to attract – притягивать).
устойчиво, и оно называется аттрактором (англ. to attract – притягивать).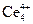 и Ce3+ в реакции Белоусова–Жаботинского. Если состояние
и Ce3+ в реакции Белоусова–Жаботинского. Если состояние 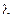 .
.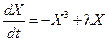 .
.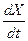 =0). Зависимость этих решений от управляющего параметра
=0). Зависимость этих решений от управляющего параметра 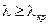 состояние системы становится неустойчивым, так как флуктуации или малые возмущения уже не гасятся, а, наоборот,
состояние системы становится неустойчивым, так как флуктуации или малые возмущения уже не гасятся, а, наоборот,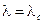 и различаются при
и различаются при 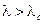 . Это явление называется бифуркацией. Таким образом, бифуркация отделяет одно устойчивое состояние от другого. В самой точке бифуркации состояние системы находится в состоянии полного хаоса, дальнейший выбор из которого делает флуктуация. Явление бифуркации ассоциируется с катастрофическими изменениями и конфликтами. Дело в том, что при
. Это явление называется бифуркацией. Таким образом, бифуркация отделяет одно устойчивое состояние от другого. В самой точке бифуркации состояние системы находится в состоянии полного хаоса, дальнейший выбор из которого делает флуктуация. Явление бифуркации ассоциируется с катастрофическими изменениями и конфликтами. Дело в том, что при 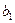 или
или  ). Определить заранее, какое состояние будет выбрано системой, невозможно.
). Определить заранее, какое состояние будет выбрано системой, невозможно.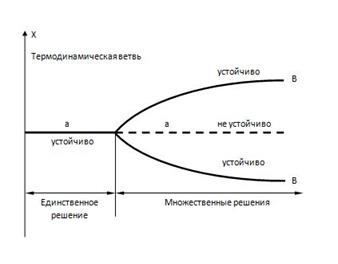 Рисунок 93
Рисунок 93
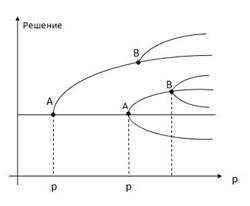 Рисунок 94
Рисунок 94



