
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концептуальные основания квантовой физикиСодержание книги
Поиск на нашем сайте
Тепловое излучение. Квантовая гипотеза Планка
С открытием электрона, рентгеновского излучения и радиоактивного распада стало очевидным, что они тесно связаны с внутриатомными процессами. В рамках классической электродинамики природа этих явлений оставалась невыясненной, что послужило катализатором развития атомной, ядерной физики и квантовой механики. Однако непреодолимые трудности встретила классическая физика при объяснении проблем теплового излучения. Именно при изучении законов теплового излучения обнаружились слабые места классической механики и электродинамики и потребовалось введение гипотезы квантов, решительным образом противоречащей всему духу классичес-кой физики. Создание квантовой механики – это такое масштабное событие XX в., что есть необ-ходимость подробнее остановиться на ее истоках. Нагретые твердые тела излучают электромагнитные волны разной длины волны. При высокой температуре тела начинают испускать видимый свет. Однако при более низкой температуре они излучают электромагнитные волны в инфракрасном диапазоне длин волн. Такое излучение называется тепловым, что подчеркивает способ его возникновения. Представим себе несколько тел, нагретых до различной температуры, и поместим их в полость, окруженную оболочкой с идеально отражающими стенками. Если даже внутри этой полости будет абсолютный вакуум, тела будут обмениваться энергией между собой посредством излучения. При этом излучение каждого тела зависит только от его собственной температуры, а не от температуры окружающих тел (закон Прево), более нагретые тела будут охлаждаться, так как они испускают большее количество энергии, чем получают от окружающих тел. В то время как менее нагретые тела будут нагреваться, поскольку они получают больше, чем отдают. Так как электромагнитные волны, излучаемые всеми этими телами, распространяются с конечной скоростью, то пространство внутри полости всегда будет заполнено энергией излучения. Опыт показывает, что со временем система приходит в состояние теплового равновесия и все тела приобретают одинаковую температуру. В этом случае тела поглощают в единицу времени ровно столько энергии, сколько отдают ее. При этом плотность излучения в пространстве достигает некоторой определенной величины, соответствующей данной температуре:
где В полости существуют электромагнитные волны всевозможных длин волн (частот). Распределение энергии излучения волн характеризуется спектральной плотностью излучения
Первый крупный шаг в теоретическом изучении свойств равновесного излучения был сделан немецким физиком Г. Кирхгофом (1824–1875), который термодинамическим путем показал, что при постоянной температуре спектральная плотность излучения Если на тело падает излучение, часть его отражается телом, а остальная часть погло-щается. Доля всей падающей энергии, заключенной в интервале длин волн Энергия, излучаемая с единицы поверхности в единицу времени, называется испус-кательной способностью и обозначается
Тело, которое поглощает все падающее на него излучение, называется абсолютно чер-ным телом ( Зная спектральную плотность можно вычислить энергию излучения и его распределение в спектре излучения абсолютного черного тела. На рисунке 53 показано распределение энергии по длинам волн для различных температур. Больцман в 1885 году открыл закон теплового излучения, который теперь называется законом Стефана–Больцмана и имеет вид
где
Экспериментальные исследования спектров излучения тел при различных температурах показали, что длина волны
Эта формула была получена В. Вином (1864–1928), в честь которого ее назвали зако-ном Вина. Согласно закону Вина максимум излучения смещается в сторону коротких длин волн с ростом температуры.
Неоднократные попытки объяснить форму спектра теплового излучения в рамках классической электродинамики заканчивались неудачей. Две такие попытки были Как видно из рисунка 54, кривая Рэлея и Джинса согласуется с экспериментом в длин-новолновой области и расходится в области коротких длин волн. В своих расчетах они исходили из теории классической статистической физики, так называемой теоремы о равнораспределении энергии по степеням свободы. Согласно этой теореме, для системы в состоянии термодинамического равновесия на каждую трансляционную и вращательную степени свободы приходится в среднем кинетическая энергия
Спектральная плотность излучения в теории Рэлея–Джинса равна
Если использовать формулу (58) для расчета энергетической светимости абсолютно черного тела, то она будет стремиться к бесконечности. Получается так, как будто излучение неограниченно растет, и равновесие между излучением и поглощением энергии никогда не наступает или наступает только при бесконечной плотности излучения. Другими словами, осцилляторы излучающего тела должны были излучать энергию до тех пор, пока их температура не упала бы до абсолютного нуля. Явление, при котором в спектре теплового излучения большая часть энергии приходится на коротковолновую область, было названо П. Эренфестом (1880–1933) «ультрафиолетовой катастрофой». Таким образом, классическая теория оказалась не в состоянии объяснить спектраль-ный состав теплового излучения и такое положение оставалось неизменным до тех пор, пока немецкий физик М. Планк не выдвинул неприемлемое с точки зрения классической физики предположение. Его идея состояла в том, что излучающие центры рассматривались как линейные гармонические осцилляторы, которые обмениваются энергией с окружающим полем излучения. Согласно гипотезе Планка, осцилляторы могут находится только в некоторых дискретных состояниях, в которых их энергия является целым кратным наименьшего количества энергии
При излучении или поглощении энергии осцилляторы переходят из одного из этих состояний в другое скачком, минуя промежуточные состояния. На основании этой гипотезы Планк в 1900 г. осуществил то, что не удалось сделать Вину, Рэлею, Джинсу и другим ученым. Он эмпирическим путем получил формулу для спектральной плотности излучения
Полученная Планком формула имеет вид
Любая формула для
Чтобы формула (59) удовлетворяла закону Вина (60), Планк вынужден был положить Таким образом, идея Планка состояла в том, что обмен энергией между излучением и веществом не происходит непрерывно, а осуществляется отдельными порциями (дискретно), так называемыми квантами, энергия которых пропорциональна частоте излучения Ввиду ничтожной малости энергии отдельного кванта дискретная природа спектра излучения остается незаметной. Формулируя свою теорию теплового излучения, Планк не располагал какими-либо прямыми доказательствами существования квантов. Единст-венной причиной выдвижения гипотезы о дискретной структуре излучения было то, что концепция квантов позволяла объяснить форму кривой распределения. Поэтому боль-шинство физиков рассматривали подход Планка к решению проблемы спектров теплового излучения как интересный трюк, не имеющий фундаментального значения. В 1900 году все еще считалось, что все физические процессы протекают непрерывно. Сам Планк не заходил так далеко, чтобы любое электромагнитное излучение считать квантованным; он считал свою гипотезу применимой только к излучению абсолютно черного тела ( Квантовая гипотеза Планка несколько лет пребывала в забвении, пока Эйнштейн не применил ее для объяснения фотоэлектрического эффекта. Эйнштейн распространил квантование энергии на все электромагнитное излучение и видел в этом естественную закономерность всеобщего характера. Не оглядываясь на господствующие в оптике волновые представления, Эйнштейн применил гипотезу Планка к свету и создал квантовую теорию света.
Квантовая (фотонная) теория света утверждала, что свет не только испускается квантами, как того требовала гипотеза Планка, но и распространяется так же – квантами. Свет может рассматриваться как поток фотонов (квантов света). Квантовая теория света не была принята многими учеными, стоящими на позициях классической физики, и среди них был родоначальник квантовой теории М. Планк. Квантовая теория света была исполь-зована Эйнштейном для объяснения законов фотоэлектрического эффекта, открытого в 1887 году Г. Герцем и подробно исследованного русским физиком А.Г. Столетовым (1839–1896), В. Гальвакcом (1859–1922) и Ф. Ленардом (1862–1947). Фотоэффект – это явление вырывания электронов из металла под действием света. С точки зрения волновой теории света, объяснение фотоэффекта было бы следующим. Свет вызывает вынужденные колебания электронов вещества, и при резонансе (равенстве частот собственных колебаний электронов и световой волны) электрон может покинуть поверхность металла. С такой точки зрения кинетическая энергия покинувшего электрона должна быть пропорциональна интенсивности света. Но в действительности энергия вырванных светом с поверхности металла электронов абсолютно не зависела от интен-сивности света. От последней зависит лишь число электронов, вылетевших из металла. Скорость же их и, следовательно, кинетическая энергия определяются частотой света, а именно, с увеличением частоты линейно увеличивается и энергия фотоэлектронов. Все эти закономерности фотоэффекта оказались непонятными с точки зрения волно-вой природы света. Эйнштейн показал, что законы фотоэффекта могут быть объяснены, если оставить классическую теорию света и предположить, что свет – это поток отдель-ных квантов (фотонов). Каждый фотон, поглощаемый металлом, отдает свою энергию электрону. При достаточно большой энергии электрон преодолевает удерживающие его в металле связи и покидает его поверхность. Поэтому энергия электрона зависит от энергии фотона, а последняя определяется частотой света. Число же фотоэлектронов пропорционально числу поглощаемых фотонов, т.е. интенсивности света, хотя и не равно ему, так как не каждый фотон срывает электрон с поверхности металла. Энергия фотона, вызывающего фотоэффект, должна соответствовать уравнению Эйнштейна
где А – работа выхода электрона из металла, В 1921 году за объяснение фотоэффекта (а вовсе не за теорию относительности, ее время еще не пришло) Эйнштейн был удостоен Нобелевской премии. В этот год Нобелевскую премию получил Р. Милликен (1868–1953) за экспериментальные работы по определению точных значений заряда электрона (е) и постоянной Планка (h). Несколько позднее (1906–1907) квантовая теория излучения была применена для объяснения теплоемкости при низких температурах. В классической физике известен закон Дюлонга и Пти, согласно которому теплоемкость твердых тел при высоких температурах не зависит от температуры и является величиной постоянной
Еще одним подтверждением реальности фотонов является эффект Комптона. Если квантовая теория света Эйнштейна верна, то фотон должен взаимодействовать со свободным электроном подобно двум сталкивающимся шарам. В 1923 году американский физик А. Комптон (1892–1962) экспериментально доказал факт существования такого взаимодействия. Если фотон с энергией
Комптон измерил К другим опытам, подтверждающим наличие корпускулярных свойств света, относятся опыт Боте и обнаружение флуктуации в световом потоке. В опыте Боте тонкая медная фольга подвешивалась между двумя счетчиками Гейгера. Фольгу возбуждали рентгеновским излучением достаточной жесткости и наблюдалось характеристическое излучение флуоресценции. Если бы энергия этого излучения распространялась в виде сферических волн, то оба счетчика должны были реагировать одновременно. Опыт показывает, однако, что этого нет: счетчики реагируют совершенно независимо один от другого. Все происходит так, как если бы возникающее излучение флуоресценции распространялось в виде направленных фотонов, которые могут попадать либо в один, либо в другой счетчик. Корпускулярные свойства света влекут за собой еще одно важное следствие: необхо-димость существования флуктуации в слабых световых потоках. Ввиду особой роли флуктуаций в процессах самоорганизации в сложных открытых неравновесных термодинамических системах, которые будут рассмотрены ниже, понятие флуктуаций требует М. Смолуховский (1872–1917), который разработал теорию броуновского движения, установил законы флуктуаций равновесных состояний в молекулярных системах. Он рассматривал следующую задачу: какова вероятность того, что все молекулы газа, находящиеся в объеме
Если
Если в качестве Вернемся теперь к флуктуациям светового потока. Действительно, если свет – это по-ток фотонов, то каждый фотон, попадая в приемное устройство (фотоэлемент, ионизаци-онную камеру или человеческий глаз), вызывает то или иное действие независимо от других фотонов. При достаточно больших интенсивностях число поглощенных фотонов Особый интерес представляет обнаружение флуктуаций слабых потоков видимого света. Такие флуктуации были обнаружены советским физиком – президентом АНССР Если среднее число фотонов во вспышках много больше порога чувствительности, то глаз будет видеть каждую вспышку, поскольку в результате флуктуаций это число не становится меньшим порога чувствительности. Однако, если глазом наблюдать вспышки, в которых среднее число фотонов находится на пороге чувствительности глаза, то произойдет следующее: вспышки, в которых число фотонов больше порога чувствительности, будут зафиксированы глазом, а вспышки, в которых число фотонов меньше порога чувствительности, не будут замечены. Таким образом, при наблюдении вспышек вблизи порога чувствительности глаза можно непосредственно визуально обнаружить флуктуации числа фотонов во вспышках. Как было установлено Вавиловым, порог чувствительности глаза в области сумеречного зрения составляет от нескольких десятков фотонов до нескольких сотен, испытывая значительные колебания для различных наблюдателей. В опытах Вавилова обнаружены флуктуации числа фотонов в световом потоке. Эксперименты, рассмотренные выше, убедительно доказывают дискретный характер электромагнитного излучения. Идеи атомизма проникли в учение о свете, в электродинамику. Казалось, континуальная физика отступила под натиском атомистических идей.
выражают связь между корпускулярными и волновыми свойствами света. Двойственная природа света получила название корпускулярно-волнового дуализма. Физика атома
К началу XX в. реальность атомов была общепризнанной. Из молекулярно-кинетичес-кой теории и различных экспериментальных данных следовало, что атомы имеют размеры порядка 10-10 м. Открытие Томсоном электрона, линейчатый спектр излучения атомов, открытие Теоретически существовали две модели строения атома. Согласно первой модели, предложенной Дж. Томсоном, по всему объему атома распределен положительный заряд. Электроны, погруженные в эту среду, взаимодействуют с элементами положительно заряженной среды атома по закону Кулона. При отклонении электрона под действием внешнего возмущения из положения равновесия возникают силы, которые стремятся возвратить его в положение равновесия. Благодаря этому возникают колебания электронов, которые порождают излучение атомов. Вторая модель приписывала атому строение, аналогичное Солнечной системе: в цент-ре находится положительно заряженное ядро, вокруг которого, подобно планетам, дви-жутся электроны, удерживаемые у ядра силами кулоновского притяжения. Этой модели придерживались Дж. Стоней, который еще в 1891 году писал: «Электроны движутся вок-руг ядра, подобно спутникам планет»; Ж. Перрен, предложивший в 1901 году «нуклеар-нопланетарную структуру атома»; японский физик Х. Нагаока, утверждавший в 1903 году, что «пространства внутри атома чрезвычайно громадны по сравнению с величинами самих, образующих его электрических ядрышек, иными словами, атом представляет своего рода сложную астрономическую систему, подобно кольцу Сатурна». Перечень подобных высказываний в пользу планетарной модели атома можно было продолжать. Однако все эти высказывания являются чисто умозрительными, натурфилософскими, не имеющими теоретической и экспериментальной основы. В науке же действует строгий принцип: открыл явление тот, кто доказал его существование. Каково строение атома в действительности, мог решить только решающий экспери-мент. Задача состояла в том, чтобы определить распределение электрического заряда в атоме по рассеянию заряженных частиц на атомах. Такой эксперимент был поставлен Согласно модели Томсона, По классической механике такая система может находится в устойчивом равновесии лишь при условии, если электроны будут обращаться вокруг ядра по определенным орбитам. Однако, с точки зрения классической электродинамики, такой атом является неустой-чивым. Это связано с тем, что электроны, движущиеся ускоренно, должны излучать электромагнитные волны, на образование которых расходуется энергия электрона. По мере уменьшения энергии электрон постепенно будет приближаться к ядру и упадет на ядро, когда вся его энергия будет израсходована. Тот факт, что атом является образованием устойчивым и спектр его излучения линейчатый, указывает на непреодолимое противоречие планетарной модели атома законам классической электродинамики. Выход из этого затруднительного положения нашел великий датский физик Нильс Бор (1885–1962) в 1913 году. Он обобщил и распространил идею Планка о квантовании энергии стационарных состояний осцилляторов на все атомные системы. Тем самым кван-товая концепция стала приобретать универсальное значение, как выражение характерной особенности внутриатомных процессов. В основу развитой им квантовой теории строения атома Бор положил планетарную модель атома Резерфорда и следующие два постулата: 1. Существуют стационарные состояния в атомах, в которых, несмотря на ускоренное движение электронов, они не излучают и не поглощают энергию. Энергия этих состояний может принимать лишь дискретный набор значений 2. При переходе из одного стационарного состояния в другое атомы испускают или поглощают квантовое излучение только строго определенной энергии. Излучение, испускаемое или поглощаемое при переходе из состояния
Это соотношение называется условием частот. Постулаты Бора, прежде всего, выражают устойчивость атомов как непреложного условия вечности материи. Он писал: «Исходным пунктом для меня была… устойчивость материи, которая, с точки зрения прежней физики, предстает подлинным чудом». Окончательно Бор утвердился в фундаментальности своей квантовой концепции при описании внутриатомных процессов после своего знакомства с формулами Бальмера и Ридберга. Между линейчатой структурой атомных спектров и идеями Планка и Эйнштейна о дискретном характере процессов испускания и поглощения света атомами он увидел глубокую связь. «Мне сразу все стало ясно, – вспоминает Бор – и после многочисленных попыток использовать квантовые идеи в более строгой форме ранней весной 1913 года мне пришло в голову, что ключом к решению атомной устойчивости являются изумительно простые законы, определяющие оптический спектр элементов». Умножением формулы Бальмера на
Выражение слева равно энергии фотона с длиной волны В основе полуквантовой (полуклассической) теории атома водорода лежит условие устойчивости орбиты из классической механики – равенство центробежной и притя-гивающей сил. В атоме водорода при движении электрона с массой m и зарядом е вокруг ядра со скоростью
Кроме указанных характеристик, вращательное движение электрона по круговой ор-бите характеризуется моментом импульса (орбитальный момент) Согласно Бору стационарными являются лишь те орбиты, при движении по которым орбитальный момент L электрона равен целому кратному постоянной Планка
Это и есть знаменитое дополнительное условие квантования Бора, которое выделяет из бесконечного множества орбит, допускаемых классической механикой, лишь дискретное множество орбит, характеризуемых условием (64). Полная энергия электрона на орбите (кинетическая плюс потенциальная)
Из условия квантования (64) и формул (60), (65) путем несложных математических преобразований можно получить величины, характеризующие движение электрона в атоме водорода. Эти величины зависят от номера орбиты следующим образом: Здесь
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.021 с.) |

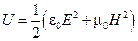 ,
,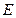 – напряженность электрического поля;
– напряженность электрического поля; 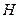 – напряженность магнитного поля.
– напряженность магнитного поля.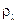 , определяемой формулой
, определяемой формулой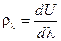 .
.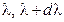 , которая поглощается телом и превращается в тепло, называется поглощательной способ-ностью тела
, которая поглощается телом и превращается в тепло, называется поглощательной способ-ностью тела 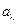 .
.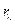 . Закон Кирхгофа гласит: Отношение испус-кательной способности тела к поглощательной пропорционально спектральной плотности излучения
. Закон Кирхгофа гласит: Отношение испус-кательной способности тела к поглощательной пропорционально спектральной плотности излучения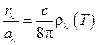 .
.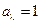 ). Для абсолютно черного тела
). Для абсолютно черного тела 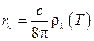 .
.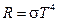 ,
,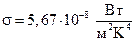 – постоянная Стефана–Больцмана; R – энергетическая свети-мость абсолютно черного тела (энергия, излучаемая единицей поверхности в единицу времени).
– постоянная Стефана–Больцмана; R – энергетическая свети-мость абсолютно черного тела (энергия, излучаемая единицей поверхности в единицу времени).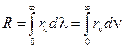 .
.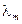 , м, на которую приходится максимум излучения, зависит от температуры Т согласно соотношению
, м, на которую приходится максимум излучения, зависит от температуры Т согласно соотношению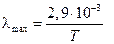 .
.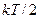 , а на колебательную степень свободы в среднем энергия
, а на колебательную степень свободы в среднем энергия 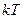 . Электромагнитное излучение внутри полости можно разложить на системы стоячих волн различной частоты. Каждая такая стоячая волна и представляет собой элементарное состояние электромагнитного поля, и по теореме о равнораспределении на каждую стоячую волну приходится средняя энергия
. Электромагнитное излучение внутри полости можно разложить на системы стоячих волн различной частоты. Каждая такая стоячая волна и представляет собой элементарное состояние электромагнитного поля, и по теореме о равнораспределении на каждую стоячую волну приходится средняя энергия 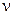 , равно
, равно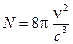 .
.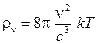 . (58)
. (58)

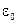
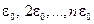 .
.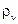 , которая полностью воспроизводила экспериментальную форму кривой распределения интенсивности в спектре излучения абсолютно черного тела для всех длин волн, а не только для длинноволновой и коротковолновой областей.
, которая полностью воспроизводила экспериментальную форму кривой распределения интенсивности в спектре излучения абсолютно черного тела для всех длин волн, а не только для длинноволновой и коротковолновой областей.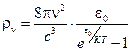 . (59)
. (59)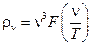 . (60)
. (60)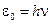 . Коэффициент пропорциональности
. Коэффициент пропорциональности 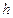 – постоянная Планка – является одной из самых важных констант современной физики. Она имеет размерность действия (Дж×с) и равна
– постоянная Планка – является одной из самых важных констант современной физики. Она имеет размерность действия (Дж×с) и равна 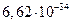 Дж×с.
Дж×с.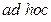 – только для данного случая) и надеялся, что проблема «ультрафиолетовой катастрофы» со временем будет решена в рамках классической физики.
– только для данного случая) и надеялся, что проблема «ультрафиолетовой катастрофы» со временем будет решена в рамках классической физики.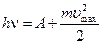 ,
,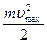 – максимальная кинетическая энергия вырванных электронов. Красная граница фотоэффекта – это максимальная длина волны фотона, при которой становится возможным явление фотоэффекта.
– максимальная кинетическая энергия вырванных электронов. Красная граница фотоэффекта – это максимальная длина волны фотона, при которой становится возможным явление фотоэффекта.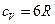 , где
, где 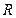 – универсальная газовая постоянная (
– универсальная газовая постоянная (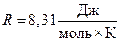 ). Согласно теории Эйнштейна теплоемкость уменьшается с понижением температуры, что находится в согласии с экспериментом. Через несколько лет теория теплоемкости Эйнштейна была существенно улучшена немецким физиком П. Дебаем. Согласно Дебаю теплоемкость при низких температурах пропорциональна кубу абсолютной температуры (
). Согласно теории Эйнштейна теплоемкость уменьшается с понижением температуры, что находится в согласии с экспериментом. Через несколько лет теория теплоемкости Эйнштейна была существенно улучшена немецким физиком П. Дебаем. Согласно Дебаю теплоемкость при низких температурах пропорциональна кубу абсолютной температуры (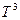 ), что привело к лучшему согласию с экспериментальными данными вплоть до самых низких температур.
), что привело к лучшему согласию с экспериментальными данными вплоть до самых низких температур.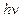 и импульсом
и импульсом 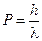 взаимодействует с покоящимся электроном как частица, то в результате столкновения он отдает часть своей энергии электрону. Вследствие этого частота рассеянного фотона уменьшится, а длина волны увеличится. В свою очередь электрон получит импульс и энергию. Теория дает следующее выражение для изменения длины волны фотона, рассеянного на угол
взаимодействует с покоящимся электроном как частица, то в результате столкновения он отдает часть своей энергии электрону. Вследствие этого частота рассеянного фотона уменьшится, а длина волны увеличится. В свою очередь электрон получит импульс и энергию. Теория дает следующее выражение для изменения длины волны фотона, рассеянного на угол 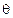 :
: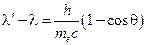 , (61)
, (61)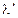 – длина волны рассеянного фотона;
– длина волны рассеянного фотона; 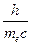 – комптоновская длина волны электрона, числовое значение ее равно
– комптоновская длина волны электрона, числовое значение ее равно 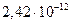 м. Эта величина представляет собой длину волны фотона, энергия которого равна
м. Эта величина представляет собой длину волны фотона, энергия которого равна 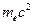 – энергии покоя электрона.
– энергии покоя электрона.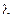 . Полученные им результаты находились в полном согласии с формулой (61). Таким образом, он доказал, что фотоны ведут себя как частицы не только при фотоэффекте, но и при их рассеянии. За эти эксперименты и их интерпретацию Комптон в 1927 году был удостоен Нобелевской премии.
. Полученные им результаты находились в полном согласии с формулой (61). Таким образом, он доказал, что фотоны ведут себя как частицы не только при фотоэффекте, но и при их рассеянии. За эти эксперименты и их интерпретацию Комптон в 1927 году был удостоен Нобелевской премии.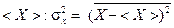 ,
, 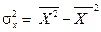 , где черта сверху означает статистическое усреднение по законам теории вероятностей для систем, состоящих из большого числа частиц. В статистической физике эквивалентной мерой флуктуаций служит относительная флуктуация
, где черта сверху означает статистическое усреднение по законам теории вероятностей для систем, состоящих из большого числа частиц. В статистической физике эквивалентной мерой флуктуаций служит относительная флуктуация 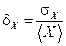 .
.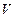 , соберутся в части
, соберутся в части 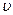 этого объема? Если бы в объеме
этого объема? Если бы в объеме 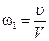 .
.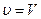 , то
, то 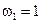 , что и должно быть, так как нахождение молекулы во всем объеме
, что и должно быть, так как нахождение молекулы во всем объеме 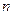 невзаимодействующих молекул, то вероятность найти
невзаимодействующих молекул, то вероятность найти 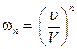 .
.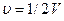 ), то
), то 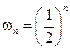 , которая для больших чисел ничтожно малая величина. Рассуждая совершенно аналогично, находим, что число частиц в некотором объеме должно испытывать случайные отклонения, флукту-ации. Если
, которая для больших чисел ничтожно малая величина. Рассуждая совершенно аналогично, находим, что число частиц в некотором объеме должно испытывать случайные отклонения, флукту-ации. Если 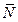 есть среднее число частиц в объеме
есть среднее число частиц в объеме 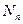 , находящихся в данный момент в этом объеме, будет, вообще-то, отличным от
, находящихся в данный момент в этом объеме, будет, вообще-то, отличным от 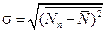 . Относительная дисперсия
. Относительная дисперсия 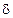 пропорциональна
пропорциональна 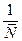 , т.е. чем больше число частиц, тем незначительнее отклонения от среднего значения
, т.е. чем больше число частиц, тем незначительнее отклонения от среднего значения 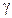 -излучений. Вследствие высокой частоты этих излучений фотоны обладают большой энергией, и даже небольшие флуктуации сказываются на интенсивности.
-излучений. Вследствие высокой частоты этих излучений фотоны обладают большой энергией, и даже небольшие флуктуации сказываются на интенсивности.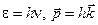
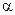 - и
- и 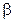 -распада, рентгеновских лучей, явление фотоэффекта и др. – все это говорило о том, что атом имеет сложное строение. На повестку дня встал вопрос о строении атома. Поскольку в целом атом электрически нейтрален, отрицательный заряд электронов должен быть скомпенсирован равным ему положительным зарядом, природа которого оставалась неизвестной.
-распада, рентгеновских лучей, явление фотоэффекта и др. – все это говорило о том, что атом имеет сложное строение. На повестку дня встал вопрос о строении атома. Поскольку в целом атом электрически нейтрален, отрицательный заряд электронов должен быть скомпенсирован равным ему положительным зарядом, природа которого оставалась неизвестной.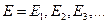 Состояния эти ха-рактеризуются своей устойчивостью; всякое изменение энергии в результате поглощения, или испускания электромагнитного излучения, или в результате соударения может происходить только скачками из одного состояния в другое, минуя промежуточные.
Состояния эти ха-рактеризуются своей устойчивостью; всякое изменение энергии в результате поглощения, или испускания электромагнитного излучения, или в результате соударения может происходить только скачками из одного состояния в другое, минуя промежуточные.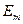 в состояние
в состояние 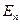 , монохроматично, и его частота
, монохроматично, и его частота 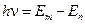 .
.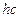 , получаем
, получаем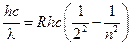 ,
, 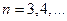 (62)
(62)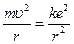 . (63)
. (63)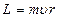 .
.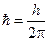 .
.
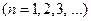 . (64)
. (64)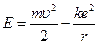 в силу равенства принимает значение
в силу равенства принимает значение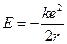 . (65)
. (65)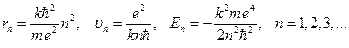
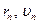 и
и 


