
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы дискретных распределений случайной величиныСодержание книги
Поиск на нашем сайте
Для дискретных случайных величин функция распределения имеет вид: F (x) = S P (X = xi), (3.28) где xi – значения случайной величины; Р – вероятности появления данного значения. Когда текущая переменная х проходит через одно из возможных значений дискретной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения. Сумма всех возможных скачков функции F (x) равна единице. График функции распределения дискретной случайной величины представляет собой ступенчатую кривую (рис. 3.1, б) В задачах надежности из дискретных распределений наиболее часто используют биномиальное распределение и распределение Пуассона. Биноминальным называют закон распределения дискретной случайной величины числа х появления событий K раз в n независимых испытаний, в каждом из которых вероятность появления событий равна Р. Вероятность того, что событие наступит ровно K раз (безразлично, в какой последовательности) определяется по формуле Бернулли:
или
где q = 1 – p – вероятность непоявления события в каждом испытании. Если число испытаний n велико, а вероятность появления событий р в каждом испытании мала, то используется формула
где а = np – среднее число (математическое ожидание) событий в n испытаниях. Распределение дискретной случайной величины Х, описываемое последней формулой, называется распределением Пуассона. Биноминальное распределение имеют, например, отказы восстанавливаемых объектов в течение заданного периода времени. Пример. На шахте работают шесть конвейеров с турбомуфтами. Вероятность безотказной работы одной турбомуфты в течение четырех месяцев q = 0,8. Найти вероятность выхода из строя в течение четырех месяцев нуля, одной, двух, трех и четырех муфт:
Пример. Цепь скребкового конвейера СП-63 имеет n = 200 соединительных звеньев. Вероятность выхода из строя соединительного звена в течение суток р = 0,01 (q = 1 – 0,01 = 0,99). Определить вероятность порыва в течение суток четырех звеньев: А = n р = 200 × 0,01 = 2;
Вероятность порыва в течение суток больше четырех звеньев
Законы непрерывных распределений Случайной величины
В теории вероятности используется много законов распределения случайной величины. К ним относятся распределения Лапласа, Коши, Стьюдента, Эрланга и многие другие. Рассмотрим распределения, наиболее часто используемые в горных процессах. Нормальное распределение. Для износовых отказов характерно нормальное распределение наработки на отказ (шахтные насосы, центрифуги и др.). Нормальное распределение характеризуется плотностью вероятности (рис.3.2)
где s2 – дисперсия;
а – математическое ожидание предельного изменения случайной величины х, –¥ < х < ¥. Функция нормального распределения описывается формулой
Обозначив
Так как
где Ф(Z) – нечетная функция, т.е. Ф(– Z) = – Ф(Z). Вероятность попадания случайной величины в заданный интервал [a, b] составит Р [a < х < b] = Пример. Наработка на отказ турбомуфты скребкового конвейера распределяется нормально с параметрами а = 500 ч и s = 100 ч. Определить вероятность безотказной работы для наработки t 1 = 200 ч и t = 700 ч:
Ф(–3) = –Ф(3) = –0,4987; Ф(2) = 0,4772; Р (200) = 1 – F (200) = 1 – (0,5 – 0,4987) = 0,9987; Р (700) = 1 – F (700) = 1 – (0,5 + 0,4772) = 0,0228. Логарифмически-нормальное распределение наработки имеют многие невосстанавливаемые изделия, например, подшипники качения. При таком распределении логарифм случайной величины х распределен по нормальному закону. Плотность вероятности:
или
где М = 0,43; s – среднеквадратичное отклонение логарифма случайной величины. Область возможных значений х лежит в интервале (0, +¥). Математическое ожидание и дисперсия случайной величины х при логарифмически-нормальном распределении (рис.3.3):
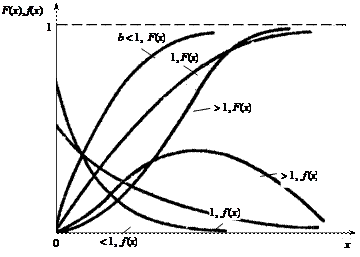
Распределение Вейбулла имеют некоторые объекты, у которых отказ наступает вследствие усталостного разрушения, многие полупроводниковые приборы. Распределение Вейбулла (рис.3.4) имеет функцию распределения
и плотность вероятности
Параметр a оказывает влияние на вид функции распределения и плотность вероятности. Экспоненциальное распределение. Распределение Вейбулла при b = 1 имеет плотность вероятности
и функцию распределения
Это распределение называется экспоненциальным и имеет особое значение в теории надежности. Наработка на отказ многих невосстанавливаемых изделий (средств автоматизации и радиоэлектронной аппаратуры и др.), у которых явление износа и старения слабо выражены, распределены экспоненциально. Вероятность безотказной работы
Интенсивность отказов
Поэтому плотность вероятности и функцию распределения при экспоненциальном распределении записывают в виде
Функция распределения Размерность l[с–1] – количество отказов в единицу времени. Можно показать, что средняя наработка до отказа Пример. Интенсивность отказов гидронасоса комбайна l = 0,0006 ч–1. Определить вероятность безотказной работы насоса за 300 ч и среднюю наработку до отказа. Вероятность безотказной работы за 300 ч
Средняя наработка до отказа
Вероятность безотказной работы при этом распределении зависит только от длины рассматриваемого интервала времени D t и не зависит от момента времени t, с которого начинается отсчет. Гамма-распределение. Если устройство состоит из одного рабочего и n резервных элементов, каждый из которых включается в работу после отказа предыдущего, то отказ устройства наступит в тот момент, когда выйдет из строя элемент n + 1. Если все элементы имеют экспоненциальное распределение с интенсивностью отказов l, то наработка до отказа всего устройства будет иметь g-распределение с параметрами l и m = n + 1. Плотность распределения случайной величины (рис.3.5) определяется из выражения
где Г – обозначение g-функции, если m – целое число, то Г(m) = = (m – 1)! Гамма-распределение наработки и времени восстановления могут иметь некоторые другие объекты, в этом случае m может быть как целым, так и дробным числом. При m = 1 g-распределение имеет плотность вероятности
т.е. экспоненциальное распределение является частным случаем g-распределения. Математическое ожидание и дисперсия случайной величины, имеющей g-распределение:
Усеченное нормальное распределение. Часто целесообразно использовать такие распределения, полученные путем ограничения интервала возможного значения случайной величины q (рис.3.6).
Минимальная наработка S > 0, максимальная S < r. Интервал наработки [ S, r ]. Случайное значение t в также заключено в некотором интервале.
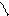 
Рис. 3.6. Усеченное нормальное распределение Если исходное распределение имеет плотность вероятности f 1(t), а усеченное – плотность вероятности f 2(t), то f 2(t) = с f 1(t). Так как при любом интервале изменения случайной величины
откуда
где F 1(r), F 1(S) – значения исходной функции в точках, соответствующих r и S. Для нормального распределения
где
При интервале [0, ¥] изменения случайной величины
Соответственно Ф(Z 2) = 0,5; Ф(Z 1) = –Ф Пример. Интенсивность отказов гидронасоса комбайна l = 0,0006 ч–1. Определить вероятность безотказной работы насоса за 300 ч и среднюю наработку до отказа. Вероятность безотказной работы за 300 ч
Средняя наработка до отказа
Контрольные вопросы
1. Понятие события и случайной величины. 2. Теоремы сложения вероятностей. 3. Теоремы умножения вероятностей. 4. Теорема вероятности появления хотя бы одного события. 5. Теорема полной вероятности. 6. Формула Бейеса. 7. Формула Бернулли. 8. Теоремы Лапласа (локальная, интегральная). 9. Наивероятнейшее число наступлений события. 10. Законы дискретных распределений случайной величины. 11. Нормальный закон непрерывных распределений случайной величины. 12. Логарифмически-нормальныйзакон непрерывных распределений случайной величины. 13. Распределение Вейбула. 14. Экспоненциальныйзакон непрерывных распределений случайной величины. 15. Гамма-закон непрерывных распределений случайной величины. 16. Усечено-нормальный закон распределений случайной величины.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.127 (0.007 с.) |

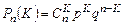 (3.29)
(3.29)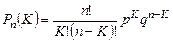 , (3.30)
, (3.30)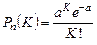 , (3.31)
, (3.31)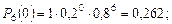
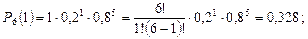
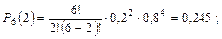
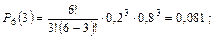
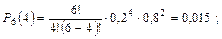

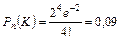 .
.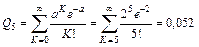 .
.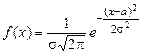 , (3.32)
, (3.32)
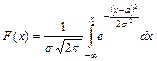 . (3.33)
. (3.33)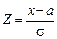 , получим
, получим 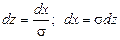 , откуда
, откуда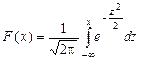 . (3.34)
. (3.34)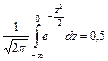 , то
, то , (3.35)
, (3.35)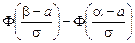 . (3.36)
. (3.36)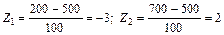 ;
;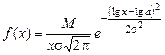 (3.37)
(3.37)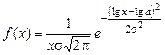 , (3.38)
, (3.38) (3.39)
(3.39)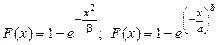 (3.40)
(3.40)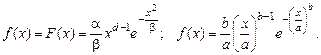 (3.41)
(3.41)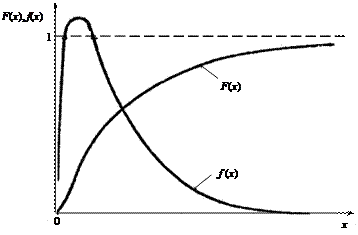
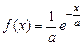 (3.41)
(3.41)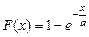 . (3.42)
. (3.42)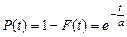 . (3.43)
. (3.43)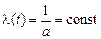 . (3.44)
. (3.44)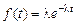 . (3.45)
. (3.45)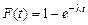 .
.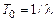 и дисперсия
и дисперсия 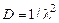 .
.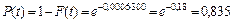 .
.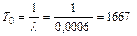 ч.
ч.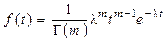 , (3.46)
, (3.46)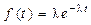 , (3.47)
, (3.47)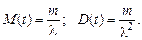 (3.48)
(3.48)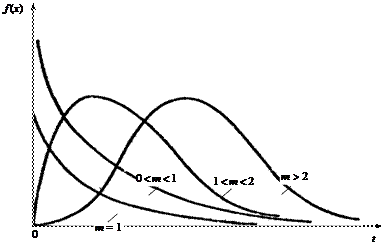

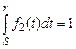 , то постоянная с может быть определена из условия
, то постоянная с может быть определена из условия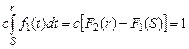 , (3.49)
, (3.49)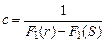 , (3.50)
, (3.50)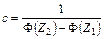 , (3.51)
, (3.51)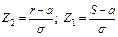 .
.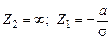 . (3.52)
. (3.52) ;
; 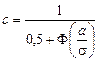 . (3.53)
. (3.53)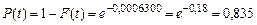 .
.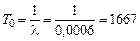 ч.
ч.


