
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация периода длительных профилактических ремонтов
Одним из методов повышения технологической надежности является профилактический ремонт машин и механизмов. Циклический характер позволяет приурочить его полностью или частично к периодам технологических перерывов в работе механизма. Профилактический ремонт позволяет уменьшить количество и длительность аварийных ремонтов, а следовательно, и простои оборудования. Однако длительный профилактический ремонт сам ведет к простою механизма и снижению его производительности. Существующие нормативные документы по проведению профилактических ремонтов не учитывают ни надежности машин, ни принятой технологической схемы. На рис. 6.8, а приведена схема комплекса оборудования, состоящего из ведущего механизма А и вспомогательного механизма Б, работающих в такой последовательности. Во время аварийного ремонта механизма А механизм Б простаивает; по окончании ремонта начинает действовать механизм Б, который работает неполный период и выполняет объем работ, подготовленный механизмом А до его ремонта. После завершения работы механизмом Б начинает снова работать механизм А. Коэффициент простоя на промежутке (0,t) выражается по формуле где Q (t) - функция распределения случайного времени исправной работы механизма А на данном промежутке; R (t) - функция надежности; a - длительность аварийного ремонта; Здесь t - время технологического перерыва механизма А (или рабочий период механизма Б). Время t принимается кратным r - рабочему периоду механизма А t = mr (m = 0, 1, 2,…). Из формулы (6.12) определяется число полных рабочих периодов m *, после которых необходим профилактический ремонт, чтобы коэффициент простоя был минимальным, m * = [t*/ r ], где t* находится как корень уравнения где Функция Q (t) определяется из опыта путем наблюдений за работой машины (рис. 6.8). Обычно опасность отказов l(t) является неубывающей функцией, исключая лишь начальный период эксплуатации машины (период приработки, когда обнаруживаются скрытые дефекты изготовления). Поэтому в качестве Q (t) принимается закон Вейбулла
для которого l0 = p/2×1/2 T ср2, Т ср - среднее время безотказной работы машины.
Рис. 6.8. Схема расчета коэффициента простоя системы машин и механизмов для различных технологических схем: 1 - профилактический ремонт; 2 - аварийный;
Для схемы, представленной на рис. 6.8, б, возможна ситуация, когда во время аварийного ремонта механизма А механизм Б также простаивает. Но после окончания ремонта сначала вновь включается механизм А, который должен работать столько времени, чтобы его суммарное время работы до аварийного ремонта r ¢ и после него Если во время аварийного ремонта механизма А механизм Б работает и выполняет объем работ, подготовленный ведущим механизмом до аварийного ремонта (см. рис. 6.8., в), то потери времени при эксплуатации комплекса равны a - q r ¢ при a > q r ¢. Тогда коэффициент простоя Следует отметить, что K п(mr) - функция, имеющая несколько минимумов; однако, задав степень точности e, можно найти требуемый минимум. Если горно-проходческий комплекс состоит из l механизмов, подверженных отказам в период их работы, то коэффициент простоя комплекса K пкомп выразится через коэффициенты простоя отдельных механизмов K п i: 1) в случае последовательной работы механизмов
где q i = ri / pi (ri - время работы i -го механизма на цикле; pi - время технологического перерыва i -го механизма на цикле); 2) в случае одновременной работы механизмов
где Оптимизация коэффициента простоя в случае последовательной работы комплекса производится по каждому механизму в отдельности. При одновременной работе нескольких механизмов формула (6.13) даст для этого варианта оценку сверху.
В случае распределения Вейбулла где В общем случае вероятности
Примеры расчета оптимального периода профилактических ремонтов Пример 1. Хронометражные наблюдения за работой комплекса для возведения набрызг-бетонной крепи дали следующие результаты: -среднее время безотказной работы узла для приготовления сухой смеси Т ср = 50 ч; -время технологического перерыва р = 6 ч; -время работы узла между технологическими перерывами -средняя длительность аварийного ремонта а = 10 ч; -средняя длительность полного профилактического ремонта Так как плотность потока отказов растет с течением времени, то в качестве закона распределения времени безотказной работы можно принять закон Вейбулла, для которого Найдем l0 для закона Вейбулла из условия Интеграл вычисляем по формуле где Для расчета оптимального числа полных рабочих периодов между профилактиками m* и минимума коэффициентов простоя K (t) можно использовать аналитический пакет MAPLE. Исходные данные: А = 10,0; Т = 50,0; R = 10,0; d = 2,0. Результаты: Количество итераций J = 3. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 3. Коэффициент простоя SK 1 = 0,1452. Следует отметить, что без профилактики K (t) = 0,2. Пример 2. Рассмотрим работу горнопроходческого комплекса, состоящего из бурового агрегата А и погрузочной машины Б. Работа этих механизмов осуществляется последовательно, и любая неисправность агрегата при нахождении его в забое должна быть устранена немедленно, прежде чем будет произведен взрыв и в забой будет введена погрузочная машина. Исходные данные: - среднее время безотказной работы бурового агрегата Т ср = 35 ч; - средняя длительность плановой профилактики - время технологического перерыва p = 6 ч; средняя длительность аварийного ремонта a = 9 ч; - время работы между технологическими перерывами r = 5 ч; - время работы до первого аварийного ремонта r ¢ = 3 ч. Выбрав закон Вейбулла Используем аналитический пакет MAPLE. Исходные данные: А = 9,0; Т = 35,0; R = 5,0; S = 2,0. Результаты:Количество итераций J = 4. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 4. Коэффициент простоя SK 1 = 0,1960. Для определения оптимального числа m * полных периодов между аварийным и профилактическим ремонтами вычисляем для ряда значений Принимая Пример 3. Погрузочно-транспортный комплекс состоит из погрузочной машины А и транспортера с бункером-накопителем Б, откуда грунт поступает в транспортные средства. В этом случае при отказе погрузочной машины уборка грунта часть времени (или все время), необходимого для аварийного ремонта, не прекращается, так как находящийся на транспортере и в бункере грунт продолжает поступать в транспортные сосуды. Пусть для погрузочной машины Т ср = 40 ч;
Тогда l0 = 0,0005; q = р /r = 2; S = 0,5 ч; a > q r. Для расчета оптимального периода m * используем аналитический пакет MAPLE. Исходные данные: А = 7,5; Т = 40,0; R = 3,0; S = 0,5; p = 6,0. Результаты:Количество итераций J = 6. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 6. Коэффициент простоя SK 1 = 0,0756. Пример 4. Рассмотрим работу бетоно-смесительного узла, состоящего из устройств для подачи материалов (заполнителей, цемента и воды) А1 через расходные бункеры в бетоносмеситель А2, из которого готовая бетонная смесь через расходные бункеры А3 перегружается в транспортные сосуды для доставки к месту бетонирования. При неисправности любого из устройств A i весь узел останавливается и возобновляет работу после ремонта отказавшего устройства. При этом устройства комплекса, следующие по технологическому процессу после ремонтируемого, сначала принимают дозу материалов или бетонной смеси, находившихся в ремонтируемом устройстве до его аварийной остановки, перерабатывают ее, а затем продолжают рабочий цикл. На основе хронометражных наблюдений нами получены следующие данные, в часах, (таблица 6.4). Используем аналитический пакет MAPLE. Исходные данные: А = 2,0; Т = 70,0; R = 16,0; S = 0,5. Результаты:Количество итераций J = 3. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 3. Коэффициент простоя SK 1 = 0,0228. Исходные данные: А = 4,0; Т = 100,0; R = 24,0; S = 0,5. Результаты:Количество итераций J = 2. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 2. Коэффициент простоя SK 1 = 0,0239. Исходные данные: А = 5,0; Т = 50,0; R = 24,0; S = 1,0. Результаты:Количество итераций J = 1. Начальное значение для поиска «М» М 1 = 1. Число полных рабочих периодов М = 1. Коэффициент простоя SK 1 = 0,0736. Отсюда по формуле (6.13) К пкомп = 0,1550. Таблица 6.4
|
|||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.193.207 (0.026 с.) |
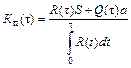 , (6.12)
, (6.12)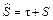 - длительность профилактического ремонта.
- длительность профилактического ремонта. , (6.13)
, (6.13) - опасность отказа.
- опасность отказа.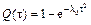 , (6.14)
, (6.14)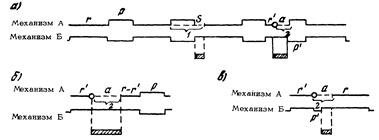
 время ремонта;
время ремонта; 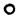 - момент отказа механизма; остальные обозначения см. на рис. 6.6
- момент отказа механизма; остальные обозначения см. на рис. 6.6 было равно полному рабочему периоду r, и только после этого включается механизм Б. В этом случае формулы (6.9) и (6.10) остаются верными, если в них заменить t на
было равно полному рабочему периоду r, и только после этого включается механизм Б. В этом случае формулы (6.9) и (6.10) остаются верными, если в них заменить t на 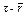 , а следовательно, t* заменить на
, а следовательно, t* заменить на 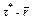 .
.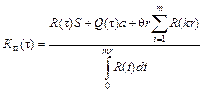
 (6.15)
(6.15)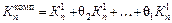 (6.16)
(6.16)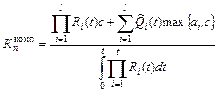 , (6.17)
, (6.17)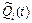 - вероятность того, что комплекс имел отказ на (0, t) вследствие аварии механизма A i; ai - продолжительность аварийного ремонта механизма A i;
- вероятность того, что комплекс имел отказ на (0, t) вследствие аварии механизма A i; ai - продолжительность аварийного ремонта механизма A i;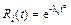 (a > 1),положив для простоты min ai ³ c, можно получить
(a > 1),положив для простоты min ai ³ c, можно получить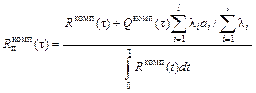 , (6.18)
, (6.18)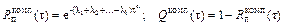 .
.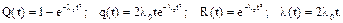
 Отсюда l0 = 0,0003 1/ч. Так как
Отсюда l0 = 0,0003 1/ч. Так как 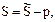 то S = 2 ч. Таким образом:
то S = 2 ч. Таким образом:

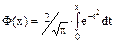 - функция Лапласа.
- функция Лапласа.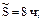
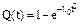 в качестве закона распределения времени безотказной работы, аналогично примеру 1 получим l0 = 0,0006, а = 9 ч, S = 2 ч, Т = 35 ч, r = 5 ч, r ¢ = 3 ч.
в качестве закона распределения времени безотказной работы, аналогично примеру 1 получим l0 = 0,0006, а = 9 ч, S = 2 ч, Т = 35 ч, r = 5 ч, r ¢ = 3 ч.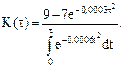
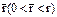 величины
величины 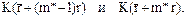
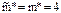 , получим
, получим 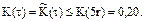
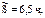 a = 7,5 ч; р = 6 ч; r = 3 ч.
a = 7,5 ч; р = 6 ч; r = 3 ч.


