Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет показателей надежности комплексов горного оборудования
Перед расчетом надежности на стадии проектирования составляется схема расчета на основе анализа процесса функционирования объекта. Затем формулируются его возможные структурные состояния и описываются возможные отказы. Расчет показателей безотказности производят с помощью теорем сложения и умножения вероятностей. Для повышения надежности применяют различные схемы резервирования. С помощью лабораторных и промышленных испытаний устанавливают соответствие расчетных и фактических показателей. При организации испытаний используют факторный план экспериментов. Пример. Структурная схема привода горной машины представлена на рисунке 6.1. 1. Основываясь на структурной схеме, найти вероятность безотказной работы горной машины Р a, если вероятность безотказной работы каждого ее элемента равна Рi.
2. Вероятность безотказной работы горной машины равна Р а. Найти вероятность безотказной работы каждого элемента, если они одинаковы. 3. Вероятность безотказной работы горной машины равна Р а. Вероятности безотказной работы последовательно включенных Р п элементов одинаковы, параллельно включенных Р пр – на 20 % меньше и тоже одинаковы. Найти вероятности безотказной работы всех элементов данной системы. 4. Вероятность безотказной работы каждого последовательно включенного элемента равна Р п, а каждого параллельно включенного на 20 % меньше Р п. Определить вероятность безотказной работы системы. Данные для расчетов: вариант 1 – Рi = 0,9; вариант 2 – Р а = 0,6; вариант 3 – Р а = 0,51; Р п = 0,73; вариант 4 – Р п = 0,73. Решение. Вариант 1. Р a = [1 – (1 – 0,9)4] × 0,9 ∙ 0,9 × [1 – (1 – 0,9)2] × 0,9 = 0,72164. Вариант 2. Это задача, обратная предыдущей, Рi = 0,849. Вариант 3. Уравнение для вычисления вероятности безотказной работы автомобиля имеет вид Р а = [1 – (1 – 0,8 Р i)4] Р i 3[1 – (1 – 0,8 Р i)2]. Для последовательного соединения Рi = 0,8342, для параллельного соединения Рi = 0,6674. Вариант4. Уравнение для расчета вероятности безотказной работы автомобиля имеет вид Р а = [1 – (1 – Р п)4](0,8 Р п)3 [1 – (1 – Р п)2]; Р а = 0,3145. Пример. В период нормальной эксплуатации горной машины, характеризуемый постоянной интенсивностью отказов, вероятность безотказной работы горной машины после Т часов работы составляет Р м. Определить интенсивность отказов l. Данные для расчетов: Т = 2500; Р м = 0,9. Для условий задачи вероятность безотказной работы определяется по формуле
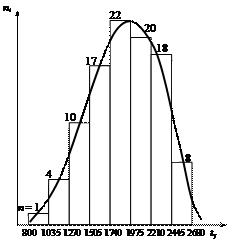
Рм = е- l t, отсюда интенсивность отказов l = –Ln(Р а)/ t = –Ln(0,9)/2500 = 0,4214 × 10–4. Расчет и построение графиков обслуживания Горной машины В расчетной работе рассмотрен вероятностный способ организации профилактических работ, основанный на анализе статистической информации о надежности. Целью расчетов является определение оптимальных сроков службы элементов горных машин, при которых достигается минимум затрат на проведение плановых и аварийных ремонтов, построение стратегии обслуживания горного оборудования и определение необходимого количества запасных частей. Порядок выполнения работы: 1. Определение параметров законов распределения случайных наработок узлов и деталей машины. 2. Выбор наиболее вероятных законов распределения наработки каждого узла машины. 3. Расчет оптимального периода замены каждого узла машины, определение сроков и видов ремонтов, выбор количества запасных частей. 4. Построение графиков ремонтов. Определение параметров распределения наработок 1-го узла выполнено путем статистической обработки накопленных данных на ЭВМ. Получены следующие результаты:
Для построения диаграммы и опытной кривой распределения наработок 1-го узла определяем длину интервала
где T maxи T min– соответственно максимальная и минимальная наработка 1-го узла машины по статистическим данным,
На рис. 6.2 представлены результаты построения диаграммы и кривой распределения наработок для 1-го узла. Наиболее вероятный закон распределения наработок каждого узла выбирается с помощью критерия согласия Пирсона c2 (табл. 6.1):
Рис.6.2. Диаграмма и опытная кривая распределения наработок 1-го узла
Таблица 6.1 Коэффициенты критерия согласия Пирсона c 2
По значению критерия согласия выбраны законы распределения: первый, второй, пятый узлы – закон Вейбулла; третий, четвертый узлы – гамма-распределения. В качестве критерия для расчета оптимальных сроков замен (табл. 6.2.) используем отношение затрат на замену узла к длительности межремонтного периода S уд и коэффициент стоимости узла Е, значение которого приведено в исходных данных. В результате расчетов на ЭВМ получены значения оптимальных сроков замены Т опт, средние значения наработок Т ср, вероятности достижения оптимальных сроков замены w и удельные стоимости замен S уд: Таблица 6.2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.254.94 (0.01 с.) |

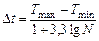 , (6.1)
, (6.1)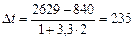 .
.