
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические основы теории надежностиСтр 1 из 37Следующая ⇒
ВВЕДЕНИЕ Надежность — это один из основных показателей качества изделий, проявляющийся во времени и отражающий изменения, происходящие в машине на протяжении ее эксплуатации. Горное оборудование на горных предприятиях открытых и подземных разработок эксплуатируется в тяжелых условиях, поэтому по отношению к нему особенно необходимо умелое содержание и своевременное проведение профилактических мер по предупреждению неисправности горных машин и электрооборудования. Поэтому разработка методологического подхода к решению вопросов надежности горных машин и оборудования, систем и их элементов является актуальной задачей. Для выполнения этой задачи необходимо создать идеологию надежности, т. е. разработать такую систему понятий и взглядов, которая позволила бы различные стороны и взаимосвязи этой многогранной проблемы объединить в одно целое и установить роль и значение всех составных частей. Статистика отказов, являющаяся до настоящего времени основным источником информации для суждения о надежности изделия — это лишь сигнал обратной связи, дающий представление о том, насколько конструкция, технология и условия эксплуатации обеспечили желаемые показатели надежности. Поэтому не статистические данные, а расчет и прогнозирование возможного поведения машины в предполагаемых условиях эксплуатации, технологическое обеспечение заданных показателей качества, специальные испытания и регламентация условий эксплуатации машин являются основой для управления надежностью и обеспечения ее требуемого уровня. Поэтому основными задачами теории надежности являются [1-10]: - изучение закономерностей возникновения отказов и восстановление работоспособности изделий; - разработка математического аппарата и методов количественного определения и сравнительной оценки надежности; - разработка мероприятий по повышению надежности; - изучение взаимосвязей между внешними воздействиями и процессами, происходящими в изделии. Ликвидация отказов различных элементов горных машин всегда сопряжена с необходимостью проведения внеплановых ремонтов в периоды рабочих смен и приводит к сокращению времени на выполнение горной машиной ее основных функций. Иногда ликвидация неисправностей оборудования может быть совмещена с технологическими простоями. Поэтому сокращение затрат времени на ликвидацию отказов горных машин тесно связано с возможностями правильной оценки технического состояния элементов и узлов машины, а также установления оптимальной периодичности технического обслуживания оборудования.
В решении всех этих задач используются математическое моделирование, методы и инструменты теории надежности горных машин и оборудования. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ Методы расчетов
Для расчета надежности используются следующие основные методы: - метод структурных схем; - метод логических схем; - схемно-функциональный метод; - матричный метод; - метод графов. Метод структурных схем. Этот метод применяется для простых систем при следующих условиях: - элементы систем рассматриваются как одноотказные; - система представляется в виде единой структурной схемы, состоящей из суммы последовательных и параллельных соединений элементов, подсистем; - в структурной схеме одно и тоже событие должно представляться в виде одного элемента, подсистемы, то есть должна соблюдаться ординарность. Методика построения структурной схемы включает следующие основные этапы: - составление на основе изучения конструкции функциональной системы принципиальной схемы системы; - составление текстовой формулировки условий безотказности системы; - составление структурной схемы, на которой прямоугольником обозначается событие безотказной работы элемента, а соединяющая линия обозначает связь - последовательность реализации событий безотказной работы системы в целом (последовательное или параллельное соединение); - составляется уравнение для оценки вероятности безотказной работы системы. Метод логических схем. Этот метод применяется: - для систем, когда трудно обеспечиваются условия независимости событий и ординарности видов отказов, то есть для сложных функциональных систем - систем с резервированием с дробной кратностью; - систем с различными видами отказов для одних и тех же элементов;
- систем, выполняющих несколько функций. Таким образом, сущность метода заключается в построении уравнения полной группы событий, характеризующих состояние работоспособности системы. Порядок определения вероятности безотказной работы при методе логических схем следующий: - формулируются условия безотказной работы системы в целом в зависимости от сочетания возможности появления отказов ее отдельных элементов; - строится логическая схема условий безотказной работы системы с цепочкой логических связей ее работоспособности и возможных отказов отдельных элементов; - составляется алгебраическое уравнение событий безотказной работы и расчетное уравнение вероятностей с использованием методов алгебры логики (алгебры Буля); - производится подбор и подготовка количественных характеристик надежности элементов, входящих в систему; - определяется вероятность безотказной работы системы в целом и отдельных ее частей. В алгебре логики используются основные операции, обозначаемые символами " + " и " х ". При логических операциях знак " + " имеет смысл " или ". Например, запись А1 + А2 означает, что имеет место событие А1 или событие А2. Знак " х " соответствует " и ". Так, если запись А1 х А2, то следует читать, что произошли или произойдут события А1 и А2. Например, в системе, состоящую из двух параллельно включенных фильтров каждый фильтр (Ф1 и Ф2) может иметь по два отказа: отказ по засорению сеток q 'ф и отказ по разрыву сеток q "ф, расчет надежности следует проводить методом логических схем. 1. Сформулируем условия безотказности (согласно порядку расчета). Система будет работать безотказно, если: а) все элементы работают безотказно; б) произойдет отказ по засорению фильтра Ф1, при условии безотказной работы фильтра Ф2; в) произойдет отказ по засорению фильтра Ф2, при условии безотказной работы фильтра Ф1. Отказ по разрыву сеток фильтров считаем недопустимым, так как при этом не будет обеспечиваться очистка рабочей жидкости от механических примесей - грязное топливо пойдет в систему. 2. Составим логическую схему безотказной работы системы. 3. Составим алгебраическое уравнение события безотказности системы. Отказ по разрыву сетки мы считаем недопустимым, но возможность его появления учитываем при помощи величины q"ф, в противном случае нельзя было бы пользоваться выражением для полной группы событий. Подставляем в уравнение для системы вероятности безотказной работы выраженные через вероятности появления отказа. Теория графов. Раздел математики, имеющий широкое практическое применение. Здесь можно сформулировать большое количество задач, связанных развитием, проектированием и эксплуатацией дискретных объектов практически во всех областях науки и техники. Формирование направления оптимизации задач теория графов получило благодаря развитию ЭВМ. Граф - форма записи комплекса, характеризуется двумя частями - отношением преобразования (преобразование энергии, переработка информации или массы с изменением свойств материала детали) и отношением связей. Связь в комплексе - то, что объединяет функциональные элементы в одно целое, она всегда жесткая (не изменяется в процессе функционирования изделия, процесса). Через связь идет обмен веществом, энергией и информацией с окружающей средой, как между элементами, так и между объектами (изделиями).
Существует несколько способов задания графа - рисунком (вершины обозначаются точками, ребра, соединяющие эти точки, - линиями), матрицей инцидентности и матрицей смежности. Граф состоит из множества х вершин и набора v пар вершин и обозначается G (x, v). Пара вершин, соединенных линиями, называется дугой или ребром графа. Ребро ориентировано - если есть стрелка, в противном случае он не ориентирован. Граф может быть смешанным. Граф Последовательность ребер Е, в которой два соседних ребра имеют общую вершину, называется маршрутом W. Произвольный граф G (x, v), где Если задано множество вершин х и соответствие Т, составляющее каждой вершине х Î Х графа множество вершин Тх, связанных с ней ребрами, то определен граф G =(XT). Для графа (рис. 1.2, б)
Рис. 1.2. Типы графов: а - ориентированный; б – неориентированный; в - смешанный
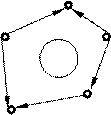
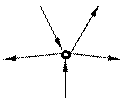
Полюсный граф одномерных элементов - ориентированный граф из одномерных элементов, является универсальной моделью информационных комплексов с сосредоточенными компонентами различной физической природы: электрической, механической, тепловой и др. (рис. 1.3). Полюсный граф строится таким образом, чтобы обеспечивались наиболее простые отношения между его структурой и уравнениями связи. Они формируются: 1. Алгебраическая сумма поперечных переменных для любой вершины графа равна нулю - S h (t)=0 (рис. 1.4, а); 2. Алгебраическая сумма продольных переменных для любого контура графа равна нулю - S x (t)=0 (рис. 1.4, б).
а)
б)
Рис. 1.3. Одномерный элемент и его полюсный граф
При алгебраическом суммировании переменных они считаются положительными, если их направления совпадают с выбранным направлением относительно вершины или контура, и отрицательными, если направления переменных противоположны выбранным направлениям.
h 4 h 1 x 5 x 3
h 5 x 4 h 1 - h 2 + h 3 + h 4 - h 5 =0 x 1 - x 2 + x 3 + x 4 - x 5 =0 а) б) Рис. 1.4. Уравнение связей для вершин (а) и контура (б)
Полюсный граф многомерных элементов. Многомерный элемент, имеющий т+1 векторных величин, посредством которых он может объединятся с другими элементами, характеризуется т независимыми поперечными переменными h 1; h 2; ...; h т и т независимыми продольными переменными x 1; x 2;...; x т . Уравнения, записанные относительно поперечных переменных:
или в матричной форме где
yg - квадратичная матрица т -го порядка.
Например, любую структуру механико-технической системы обычно рассматривают в терминах теории графов, т.е. в виде ориентированного графа, вершины которого соответствуют аппаратам, а дуги – потокам (рис. 1.5), номера вершин обозначены курсивом (справа сверху от вершины), а номера потоков – малым прямым шрифтом (под линией соответствующего потока).
Рис. 1.5. Представление механико-технической системы в виде ориентированного графа
Последовательность сцепленных дуг, позволяющая пройти от одной вершины к другой, называется путем. Путь можно обозначить как через последовательность дуг, так и через последовательность вершин. Путь, начальная вершина которого совпадает с конечной, причем каждая вершина, за исключением начальной, проходится только один раз, называется контуром. Например, на рис. 1.5 имеются три контура (по вершинам): 2-3-4-2, 3-4-3 и 6-7-6. Комплексом, называется часть графа, вершины которого обладают следующими свойствами: - каждая из вершин и дуг комплекса входит в один из контуров графа; - если вершина i входит в комплекс, то в этот комплекс входят также все вершины, входящие в контуры, которые содержат вершину i. Например, на графе, представленном на рис. 1.5, имеются два комплекса (по вершинам): 2-3-4 и 6-7. В первый комплекс входят два контура (2-3-4-2 и 3-4-3), а во второй – один (6-7-6). Примеры математических моделей теории надежности. Модель надежности системы - математическая модель, устанавливающая связь между показателями надежности системы, характеристиками надежности элементов, его структуры и параметрами ее процесса функционирования. Модель отказа - математическое описание физических и (или) химических процессов, составляющих механизм отказа. Модели, построение которых позволит раскрыть процессы распределения отказов и даст возможность оценить надежность систем на стадии проектирования, эксплуатации, должны учитывать степень опасности, то есть возможность сравнения с нормами надежности.
Одна из классификаций моделей надежности включает в себя модели применительно к постепенным и внезапным отказам для невосстанавливаемых и восстанавливаемых систем однократного и многократного использования, то есть различают две группы моделей надежности: - модели надежности, учитывающие постепенные отказы. При них протекание различных процессов повреждения приводит к изменению во времени отказоопасного параметра. Обычно удается ограничиться 1-2 параметрами. Характерным примером постепенных отказов являются случаи воздействия износа и старения на состояние работоспособности; - модели надежности, учитывающие внезапные отказы. Причина возникновения внезапных отказов не связана с изменением состояния систем в период времени его предыдущей работы или хранения, а зависит от уровня внешних воздействий, связана с неблагоприятным сочетанием внешних факторов, то есть построение моделей связано с условиями эксплуатации системы, режимами работы, с вероятностью возникновения экстремальных нагрузок. В модели надежности системы находят отражение только те свойства или характеристики элементов и только те их взаимные связи в системе, которые являются существенными с позиции надежности. Модели надежности систем подразделяются на модели параметрические и на модели в терминах отказов элементов. Параметрические модели надежности (как правило характерны для простых систем) строятся на представлении выходной характеристики в виде функции случайных параметров элементов (параметры как случайные функции времени). Система считается не отказавшей, если ее выходные параметры в течение заданного времени находятся в установленных пределах. Модели в терминах отказов элементов являются основными при исследовании надежности сложных систем. Модель отражает при четком определении понятия отказа для всех элементов системы влияние отказов элементов системы на надежность системы. По принципам построения модели подразделяются на: - аналитические (для простых задач определения зависимостей между параметрами системы и показателями надежности); - статистические (при взаимодействии большого числа факторов, при решении сложных задач); - комбинированные (аналитические модели для частей задачи и статистические модели задачи в целом). Модели надежности элементов по степени детализации учета факторов подразделяются на: - модели типа "нагрузка-прочность" (в качестве нагрузок рассматриваются тепловые, механические, электрические, радиационные и др.); - модели типа "распределение времени". Из множества законов распределения случайных величин, разработанных в теории вероятностей, наибольшее значение для теории надежности имеют пять законов: -экспоненциальный, -нормальный, -Вейбулла, -Пуассона, -биномиальный. Для описания сложных многофункциональных систем применяются комбинации этих законов. Экспоненциальное распределение (для непрерывных случайных величин). Является одним из самых простых и удобных законов распределения для анализа надежности сложных многоэлементных технических систем при оценке их работы на малых интервалах времени, сопоставимых со временем выполнения задания, и когда каждому задействованию системы предшествует строго регламентированное техническое обслуживание. Нормальное распределение (закон Гаусса). Закон занимает исключительное место в теории надежности: - как средство описания случайных событий износа и старения для малоэлементных простых систем; - он является пределом, к которому при стремлении к бесконечности числа испытаний приближаются другие законы; - ему подчиняются независимые случайные величины, сумма которых чем больше, тем точнее подчинение нормальному закону. Распределение Вейбулла (для непрерывных случайных величин). Распределение Вейбулла было получено экспериментально. Может быть использовано для описания безотказности объектов в течение всех трех типовых периодов эксплуатации: приработка, установившаяся эксплуатация и старение. Используется для исследования распределения ресурсов и сроков службы. Распределение Вейбулла как частный случай при m = 1 включает распределение экспоненциальное, Релея, близкое к нормальному. Распределение Пуассона (для дискретных случайных величин). Это распределение используется в теории надежности, когда представляет интерес появление некоторого дискретного числа одинаковых событий. Появлению каждого события (отказа) соответствует некоторая точка на временной шкале. Биномиальное распределение - распределение Бернулли (для дискретных случайных величин). Часто используется для определения вероятности дискретных случайных величин, положительных и целых, таких случайных событий, как общее число неудачных исходов в последовательности n испытаний. Биномиальное распределение применяется при статистическом контроле качества выборки изделий (не больше 10 % от объема всей партии) или при определении количества отказов невосстанавливаемых изделий в течение заданного времени при испытаниях. При очень малых значениях q биномиальное распределение может быть заменено распределением Пуассона (nq < 0,2), а при больших значениях (nq > 20) - нормальным распределением. В зависимости от наличия статистической информации об отказах изделия в теории надежности используются теоретические (см. выше), либо статистические описательные модели (например, в виде гистограмм), которые строятся на основе математического описания истинных механизмов, процессов, влияющих на отказ. Теоретические модели позволяют описать явления во всем диапазоне его возможного развития и изучать поведение системы в условиях, в которых еще не были поставлены эксперименты. Теоретические модели, следовательно, могут быть отнесены к прогнозным моделям. Для обоснованного выбора типа теоретического распределения времени наработки на отказ целесообразно использовать статистическую информацию по отказам. Выбранному теоретическому распределению времени наработки должна соответствовать определенная модель приближения изделия к отказу. Выявление такого соответствия зависит от вида и назначения исследуемых изделий.
Контрольные вопросы
1. Какие измеряемые параметры в определении надежности вы знаете? 2. Какие специфические особенности вопросов надежности рассматриваются? 3. С чем связано абсолютное изменение качества? 4. С чем связано относительное изменение качества? 5. Какие трудности возникают при оценке надежности машин? 6. С чем связаны проблемы надежности? 7. Какие направления развития науки и исследований по надежности, вы заете? 8. На каких науках базируется теория надежности? 9. Как изменяется экономическая эффективность машины во времени? 10. Понятия случайных: события, величины, процесса, закона. 11. Сущность закона распределения случайной величины. 12. Для чего производятся расчеты надежности? 13. Классификация видов расчетов надежности? 14. Какие основные методы расчетов надежности, вы знаете? 15. Опишите метод структурных схем. 16. Этапы построения структурных схем. 17. Опишите метод логических схем. 18. Опишите порядок определения вероятности безотказной работы при методе логических схем. 19. Опишите схемно-функциональный метод. 20. Опишите матричный метод. 21. Опишите метод графов. 22. Расчет надежности простых систем методом структурных схем. 23. Количественные показатели надежности. 24. Способы резервирования и методы расчета надежности при различном резервировании. 25. Направления совершенствования расчетных методов. 26. Понятие параметрической надежности. 27. Виды математических моделей надежности. 28. Этапы математического моделирования надежности. 29. Охарактеризовать микроуровни; макроуровни и метауровни математического моделирования. 30. Классификация математических моделей надежности. 31. Характеристика наиболее значимых законов распределения случайных величин, разработанных в теории вероятностей.
ОСНОВНЫЕ ПОНЯТИЯ И МАТЕМАТИЧЕСКИЕ ОСНОВЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ГОРНЫХ МАШИН И ОБОРУДОВАНИЯ Основные понятия Терминология по надежности в технике распространяется на любые технические объекты - изделия, сооружения и системы, а также их подсистемы, рассматриваемые с точки зрения надежности на этапах проектирования, производства, испытании, эксплуатации и ремонта. В соответствии с ГОСТ 21.002-83 под надежностью понимают свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования. Надежность является комплексным свойством, которое в зависимости от назначения объекта и условий его применения может включать безотказность, долговечность, ремонтопригодность и сохраняемость или определенные сочетания этих свойств. Для оценки надежности объекта используют показатели надежности – это количественная характеристика одного или нескольких свойств, составляющих надежность объекта, а именно: - безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторого времени или некоторой наработки; - долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания (ТО) и ремонта; - ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин его отказов, повреждений и устранений их последствий путем проведения ремонта и ТО; - сохраняемость – свойство объекта непрерывно сохранять исправное и работоспособное состояние в течение и после хранения и (или) транспортирования. Объект – предмет назначения и практической деятельности человека. В теории надежности рассматриваемые объекты определенного целевого назначения являются результатом производственной деятельности человека: изделие, система, элемент. Изделие расходует свой ресурс, продукт расходуется сам. Изделие рассматривается в периоды проектирования, изготовления, эксплуатации, исследований, испытаний на надежность. Техническая система является множеством элементов, взаимосвязанных функционально и взаимодействующих друг с другом в процессе выполнения определенного круга задач. Элемент – простейшая в рамках конкретного рассмотрения составная часть системы. Исправное состояние (и справность ) – состояние объекта, при котором он соответствует всем требованиям нормативно-технической и (или) конструкторской (проектной) документации. Неисправное состояние ( неисправность) – состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и (или) конструкторской (проектной) документации. Работоспособное состояние ( работоспособность ) – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской (проектной) документации. Работоспособный объект в отличие от исправного должен удовлетворять лишь тем требованиям нормативно-технической и (или) конструкторской (проектной) документации, выполнение которых обеспечивает нормальное применение объекта по назначению. Работоспособный объект может быть неисправным, например, если он не удовлетворяет эстетическим требованиям, причем ухудшение внешнего вида объекта не препятствует его применению по назначению. Неработоспособное состояние ( неработоспособность) – состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации. Для сложных объектов возможно деление их неработоспособных состояний. При этом из множества неработоспособных состояний выделяют частично неработоспособные состояния, при которых объект способен частично выполнять требуемые функции. Так же для сложных объектов возможны частично неработоспособные состояния, при которых объект способен выполнять требуемые функции с пониженными показателями или способен выполнять лишь часть требуемых функций. Предельное состояние – состояние объекта, при котором его дальнейшая эксплуатация или восстановление его работоспособного состояния невозможно или нецелесообразно. В зависимости от условий эксплуатации для одного и того же объекта могут быть установлены два и более критериев предельного состояния. Данные понятия охватывают основные технические состояния объекта. Каждое из них характеризуется совокупностью значений параметров, описывающих состояние объекта, а также качественных признаков, для которых не применяют количественные оценки. Номенклатуру этих параметров и признаков, а также пределы допустимых их изменений устанавливают в нормативно-технической и (или) конструкторской (проектной) документации. В теории надежности имеют место временные понятия. Наработка – п родолжительность или объем работы объекта. Наработка может быть как непрерывной величиной (продолжительность работы в часах, километраж пробега и т. п.), так и целочисленной величиной (число рабочих циклов, запусков и т. п.). Наработку объекта, работающего непрерывно можно измерять в единицах календарного времени. Если объект работает с перерывами, то различают непрерывную и суммарную наработку. В этом случае наработку также можно измерять в единицах времени. Для многих объектов физическое изнашивание связано не только с календарной продолжительностью эксплуатации, но с объемом работы объекта, и поэтому зависит от интенсивности применения объекта по назначению. Для таких объектов наработку обычно выражают через объем произведенной работы или число рабочих циклов. Если трактовать понятие "время" в обобщенном смысле - как параметр, служащий для описания последовательности событий и смены состояний, то принципиальная разница между наработкой и временем отсутствует даже в том случае, когда наработка является целочисленной величиной (например календарное время тоже отсчитывают в днях, месяцах и т. п.). Поэтому наработка и родственные ей величины (ресурс, остаточный ресурс) отнесены к категории временных понятий. Наработка до отказа – н аработка объекта от начала эксплуатации до возникновения первого отказа. Наработка между отказами – н аработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Времявосстановления – п родолжительность восстановления работоспособного состояния объекта. Наработка до отказа вводится как для неремонтируемых (невосстанавливаемых), так и для ремонтируемых (восстанавливаемых) объектов. Наработка между отказами определяется объемом работы объекта от k -го до (k +l)-гo отказа, где k =1, 2... Эта наработка относится только к восстанавливаемым объектам.
Показатели безотказности Безотказность – вероятность того, что в пределах заданной наработки отказа объекта не возникнет. Показатели безотказности невосстанавливаемых объектов: - вероятность безотказной работы Р (t 0) – вероятность того, что в пределах заданной наработки отказ объекта не возникнет; - интенсивность отказов l(t)– условная плотность возникновения отказа, определяемая для рассматриваемого момента времени при условии, что до этого отказ не возник; - средняя частота отказоw(t); - средняя наработка до отказа T 0 – математическое ожидание наработки до первого отказа; - наработка на отказ Т – среднее время между соседними отказами для восстанавливаемых изделий. Математическое определение вероятности безотказной работы от начала эксплуатации до t 0 (рис.2.1): - вероятностное
где
- статистическое
где
Рассмотрим это на примере:
Если отсчет времени работы производится от произвольного момента t, то вероятность безотказной работы в интервале времени от t до t + t 0 может быть определена на основании теоремы умножения вероятностей. Действительно,
вероятностный способ определения:
где Статистический способ определения:
Рис.2.1. Определение безотказности: а – вероятностное; б – статистическое Пример. На угольном разрезе при эксплуатации из 10 участковых насосов в течение года отказали 3.Определить вероятность безотказной работы за год.
Таким образом, При вероятности отказа в интервале времени от 0 до t 0: - вероятностное определение:
где Q (t 0) – вероятность того, что объект откажет в течение заданного времени t 0, начав работу при t = 0, или того, что случайное время работы объекта до отказа окажется меньше заданного времени t 0; очевидно, что Q (t 0) = 1 – Р (t 0), так как события несовместны; - статистическое определение
При вероятности отказа в интервале времени от t до t + t 0: - вероятностное определение: - - статистическое определение:
где D n (t, t 0) – число общих отказов именно в интервале времени (t, t + t 0). Плотность распределения отказов объекта расчитывается: - вероятностное определение:
где f (t) – плотность вероятности того, что время работы объекта до отказа меньше t, или плотность вероятности отказа к моменту времени t; - статистическое определение:
|
||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.145 с.) |
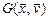 - ориентирован, если порядок концевых вершин существенен и состоит из ориентированных ребер (рис. 1.2, а). Граф G (x, v) - неориентирован, если порядок концевых вершин несущественен и состоит из неопределенных ребер (рис. 1.2, б). Граф
- ориентирован, если порядок концевых вершин существенен и состоит из ориентированных ребер (рис. 1.2, а). Граф G (x, v) - неориентирован, если порядок концевых вершин несущественен и состоит из неопределенных ребер (рис. 1.2, б). Граф 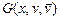 - смешанный и содержит ориентированные и неориентированные ребра (рис. 1.2, в).
- смешанный и содержит ориентированные и неориентированные ребра (рис. 1.2, в).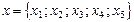 ;
; 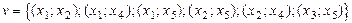 показан на рис. 1.2, б.
показан на рис. 1.2, б.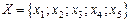 , а
, а 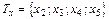 , (1.1)
, (1.1)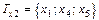 ,
, 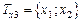 ,
, 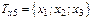 . (1.2)
. (1.2)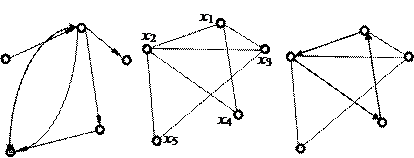

 h 2 h 3 x 1 x 2
h 2 h 3 x 1 x 2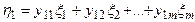 ,
,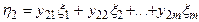 , (1.3)
, (1.3)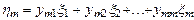 ,
,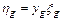 ,
,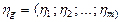 - вектор поперечных переменных;
- вектор поперечных переменных;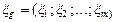 - вектор продольных переменных;
- вектор продольных переменных;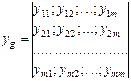 . (1.4)
. (1.4)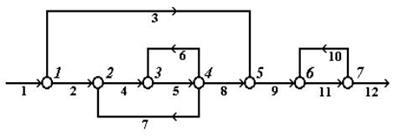
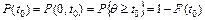 , (2.1)
, (2.1)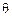 – случайное время работы (наработки) объекта до отказа (между отказами);
– случайное время работы (наработки) объекта до отказа (между отказами);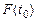 – функция распределения случайной величины
– функция распределения случайной величины 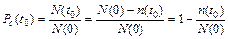 , (2.2)
, (2.2)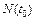 – количество исправленных объектов в момент времени t 0;
– количество исправленных объектов в момент времени t 0;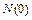 – количество исправленных объектов в момент времени t = 0;
– количество исправленных объектов в момент времени t = 0; 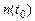 – количество отказов объектов за время t 0.
– количество отказов объектов за время t 0.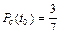 ;
; 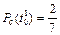 или
или 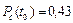 ;
; 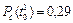 ;
;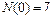 ;
; 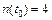 ;
; 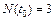 .
.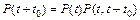 . (2.3)
. (2.3)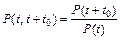 , (2.4)
, (2.4)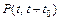 – вероятность того, что объект проработает безотказно в течение заданного времени t 0, начиная с момента времени t, или условная вероятность того, что случайное время работы до отказа окажется больше t + t 0 при условии, что объект уже проработал безотказно до момента времени t.
– вероятность того, что объект проработает безотказно в течение заданного времени t 0, начиная с момента времени t, или условная вероятность того, что случайное время работы до отказа окажется больше t + t 0 при условии, что объект уже проработал безотказно до момента времени t.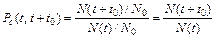 , (2.5)
, (2.5)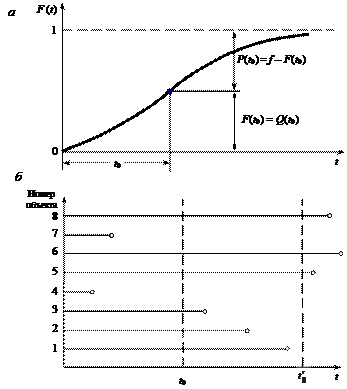 где
где 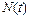 – количество объектов, исправленных к моменту времени t.
– количество объектов, исправленных к моменту времени t.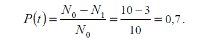
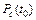 – отношение числа объектов, безотказно проработавших до момента времени t 0, к числу объектов, исправленных в начальный момент времени t = 0, или частость события, состоящего в том, что реализация времени работы объекта до отказа окажется больше заданного времени работы t 0.
– отношение числа объектов, безотказно проработавших до момента времени t 0, к числу объектов, исправленных в начальный момент времени t = 0, или частость события, состоящего в том, что реализация времени работы объекта до отказа окажется больше заданного времени работы t 0.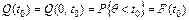 , (2.6)
, (2.6)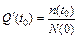 . (2.7)
. (2.7)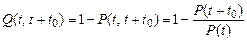 ; (2.8)
; (2.8)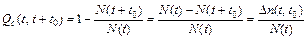 , (2.9)
, (2.9)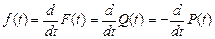 , (2.10)
, (2.10)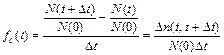 .
. 


