Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы статистической термодинамикиСодержание книги
Поиск на нашем сайте
Статистическая термодинамика позволяет рассчитать термодинамические функции газообразных веществ (внутреннюю энергию, энтальпию, теплоемкость, энтропию, энергии Гиббса и Гельмгольца) на основании известных молекулярных констант, т.е. характеристик отдельной молекулы. Для этой цели в статистической термодинамике вводится функция
Эта функция называется суммой по состояниям или функцией распределения, так как она показывает, как распределяются молекулы идеального газа по соответствующим значениям энергии. В принципе состоянию с одним значением энергии Внутреннюю энергию 1 моля идеального газа, находящегося в системе при постоянном объеме (V =const), можно выразить через сумму по состояниям
Так как все термодинамические функции связаны между собой, то, используя уравнение (5.2), можно получить уравнения для других термодинамических функций. Так, например, изохорная теплоемкость газа
Абсолютная энтропия
Энергия Гельмгольца
Полная энергия газовой молекулы складывается из энергии поступательного движения центра тяжести молекулы Епост, вращательной энергии атомов вокруг центра тяжести Евр, колебательной энергии Екол и электронной энергии Еэл, т.е.
Поэтому нетрудно показать, что
или
Соответственно, термодинамические функции можно представить как сумму составляющих, относящихся к различным видам движения. Используя данные по строению отдельной молекулы, можно вычислить составляющие суммы по состояниям для отдельных видов движения. Для поступательного движения эта величина зависит от массы частицы М, температуры Т и давления Р (или объема V):
или
Пример:. Рассчитаем значение поступательной составляющей суммы по состояниям для молекулярного водорода при Р=1 атм и Т=298К. Решение: Если молярную массу М выражать в г/моль, а давление Р в Па, то в уравнении (5.7) const=8.8612 и тогда
Для вращательного движения двухатомной или линейной многоатомной молекулы составляющая суммы по состояниям зависит от величины момента инерции молекулы I, температуры и коэффициента симметрии s:
Для вращательного движения многоатомной нелинейной молекулы типа ассиметричного волчка, имеющего различающиеся моменты инерции относительно всех трех осей симметрии, составляющая суммы по состояниям равна
Пример:. Рассчитаем значение вращательной составляющей суммы по состояниям для молекулы водорода при Т=298К. Решение:. Для двухатомной молекулы момент инерции рассчитывается по формуле
где Для молекулы водорода
Равновесное межъядерное расстояние для молекулы водорода
Коэффициент симметрии для линейных молекул
Колебательную составляющую суммы по состояниям можно вычислить по уравнению:
где q - характеристическая температура, зависящая от собственной частоты колебания связи в молекуле При расчете колебательных составляющих термодинамических функций часто пользуются таблицами Эйнштейна, в которых приводятся значения этих функций в зависимости от величины приведенной характеристической температуры Значения При температурах меньше 2000К электронная составляющая суммы по состояниям определяется вырождением невозбужденного основного состояния
Величина Статистическая термодинамика позволяет рассчитать теплоемкость идеального газа при различных температурах. Изобарную молярную теплоемкость можно представить в виде суммы составляющих
Используя уравнения (6.2) и (6.3), нетрудно показать, что для идеального газа
Это выражение совпадает с величиной, полученной в рамках классической механики, согласно которой на одну степень свободы движения приходится энергия равная Изохорная теплоемкость Для двухатомных и линейных многоатомных молекул
и вращательная составляющая теплоемкости Для многоатомных несимметричных нелинейных молекул Значения теплоемкости газа, также как и в случае поступательного движения, соответствует представлениям классической механики, согласно которым на одну степень свободы движения приходится значение теплоемкости равное
Таким образом, для двухатомной или линейной многоатомной молекулы
Для нелинейной многоатомной молекулы
Электронная составляющая теплоемкости Следовательно, расчет теплоемкости сводится к нахождению колебательной составляющей для каждого вида колебания.
Пример:. Рассчитать изобарную молярную теплоемкость водорода при Т=298К и 1000К. Решение:. Для молекулы водорода волновое число собственных колебаний Для нахождения колебательной составляющей теплоемкости воспользуемся таблицами Эйнштейна (КС, табл. 46, с.93). При
При
Пример:. Рассчитаем изобарную молярную теплоемкость метана при 500К. Решение:. Молекула метана – нелинейная многоатомная молекула. В табл. 110, с.187 [2] приведены волновые числа собственных колебаний многоатомных молекул и соответствующие им характеристические температуры. Молекула метана имеет 9 колебательных степеней свободы, причем некоторые колебания вырождены, т.е. характеризуются одним и тем же волновым числом. Следовательно, для метана В таблице 5.1 приводятся результаты расчета колебательной составляющей изобарной теплоемкости метана при Т=500К.
Таблица 5.1 – Расчет колебательных составляющих изобарной теплоемкости для молекулы метана
Таким образом суммарное значение колебательной составляющей составляет Классическая термодинамика позволяет определить теплоемкость газа при различных температурах, используя интерполяционные уравнения:
при этом коэффициенты Для метана расчет изобарной теплоемкости по интерполяционному уравнению 5.1 Многовариантное задание № 13 «Расчет теплоемкости идеального газа»
Используя спектральные данные, вычислить теплоемкость идеального газа А при температуре Т (таблица 5.2). Полученный результат сравнить с величиной, рассчитанной с использованием интерполяционных уравнений. 5.2 Контрольные вопросы
1. Что показывает сумма по состояниям? Что такое статистический вес? 2. С какой термодинамической функцией связана сумма по состояниям? 3. Как представить сумму по состояниям в виде составляющих по различным видам движения молекулы? 4. От каких параметров зависит поступательная составляющая суммы по состояниям? 5. От каких молекулярных констант зависит вращательная составляющая суммы по состояниям? 6. С какой молекулярной константой связана характеристическая температура? Для вычисления какой составляющей суммы по состояниям необходимо рассчитывать эту величину? 7. Как рассчитать колебательную составляющую суммы по состояниям для многоатомной молекулы? 8. От чего зависит электронная составляющая суммы по состояниям? 9. Какие термодинамические функции можно рассчитать, используя сумму по состояниям? 10. Какие составляющие термодинамических функций можно определить, используя таблицы Эйнштейна? 11. Как вычислить изобарную молярную теплоемкость газа методом статистической термодинамики? Таблица 5.2 – Варианты заданий
ХИМИЧЕСКАЯ КИНЕТИКА
Важнейшей количественной характеристикой химического процесса является скорость химической реакции. Под средней удельной скоростью химическойреакции, определенной по i -тому компоненту, понимают изменение количества этого компонента за единицу времени в единице реакционного пространства. Для гомогенной реакции за реакционное пространство принимается объем. Тогда для бесконечно малого промежутка мгновенную удельную скорость реакции (υ i ) можно выразить: где ni – количество i -го вещества, в молях; V – объем реакционной смеси; t – время. Так как скорость всегда положительна, то для веществ, расходующихся в ходе реакции, dni < 0и Если гомогенная реакция протекает в замкнутой системе при V = const, то в этом случае V можно внести под знак дифференциала и, учитывая, что ni / V = ci, уравнение (6.1) можно представить в виде: где с i - концентрация вещества (обычно в моль/л).
Для определения скорости реакции по i – тому компоненту необходимо знать, как изменяется концентрация этого компонента во времени в ходе реакции. График зависимости концентрации вещества от времени называют кинетической кривой. Скорость реакции в любой момент времени определяется как тангенс угла наклона касательной, проведенной к кинетической кривой в данный момент времени. Скорость химической реакции зависит от целого ряда факторов. При заданных внешних условиях (температура, давление, среда, в которой происходит реакция) скорость является функцией концентрации реагирующих веществ. Для протекания химической реакции реагирующие частицы должны столкнуться или, по крайней мере, сблизиться друг с другом. Число столкновений частиц пропорционально их концентрации. Тогда для скорости химической реакции a А + b B ® продукты можно записать уравнение: υ =
Уравнение (6.3) называется кинетическим уравнением. Это основное уравнение формальной гомогенной кинетики. Параметр k – коэффициент пропорциональности – константа скорости химической реакции. Константа k характеризует скорость химической реакции при концентрациях реагирующих веществ, равных единице: k = υ при с А = с B = 1. Константа скорости химической реакции зависит от физико-химических свойств веществ, участвующих в реакции, от среды, в которой она происходит, от наличия катализатора или ингибитора, от температуры, и не зависит от концентрации реагирующих веществ. Поэтому, если хотят сравнивать скорости химических реакций, то всегда сравнивают константы скорости этих реакций. Параметры n Аи n B называют порядком реакции по веществу А и B, соответственно. Общий (полный) порядок реакции n = n А + n B . Порядки реакции – это эмпирические показатели степени в кинетическом уравнении, которые находятся из экспериментальных данных. Порядки сложных реакций, состоящих из нескольких стадий, могут быть любыми: целыми, дробными, нулевыми, отрицательными. Порядки ni, как правило, не совпадают со стехиометрическими коэффициентами (а и b). Причина этого заключается в том, что химические реакции обычно идут в несколько стадий. Простые реакции протекают в одну элементарную стадию. Сложные химические реакции состоят из нескольких элементарных стадий. Молекулярностью отдельной стадии химической реакции называют наименьшее число частиц, которые должны столкнуться, чтобы произошла данная химическая реакция. Это целое число – 1, 2, 3, которое совпадает с суммой стехиометрических коэффициентов для данной стадии химической реакции. Молекулярность не может быть больше 3, так как вероятность одновременного столкновения четырех частиц в данной точке пространства крайне мала. Для химической реакции, протекающей в одну стадию, порядки реакции по веществам совпадают со стехиометрическими коэффициентами, а общий порядок совпадает с молекулярностью реакции. Если в сложной реакции скорость какой-либо стадии значительно меньше, чем скорость других стадий, то такая стадия называется лимитирующей, и скорость этой стадии определяет скорость всего процесса. В этом случае молекулярность лимитирующей стадии совпадает с общим порядком реакции. Наиболее часто химические реакции протекают по первому или второму порядку. Первый, второй и третий порядки реакций наблюдаются в двух случаях: 1. Реакция простая, протекающая в одну стадию. 2. Сложная реакция имеет лимитирующую стадию. Число простых реакций очень мало. Значительно больше реакций, имеющих лимитирующую стадию. Именно скорость этой стадии определяет общую скорость химической реакции. Тогда порядок химической реакции будет равен порядку лимитирующей стадии. Используя основное уравнение кинетики (6.3), можно получить выражение для расчета константы скорости химической реакции различных порядков. Алгоритм решения этой задачи следующий: а) Записывают кинетическое уравнение. б) Разделяют переменные с и t. в) Интегрируют полученное уравнение в пределах от начала реакции (t = 0) и начальной концентрации с 0 до момента времени τ и концентрации с. Для реакции первого порядка основное кинетическое уравнение имеет вид После интегрирования получают уравнение Размерность k – c-1 или мин -1. Из уравнения (6.4) следует, что зависимость ln c от t линейна. Период полупревращения (t 1/2) – это время, за которое концентрация исходного реагирующего вещества уменьшается вдвое. Для реакции первого порядка Следовательно, период полупревращения реакций первого порядка не зависит от начальной концентрации реагирующего вещества. Таким образом, если анализ экспериментальных данных показывает, что для исследуемой реакции зависимость ln c от времени линейна, и период полупревращения не зависит от начальной концентрации, то данная реакция первого порядка. Реакции второго порядка в общем виде можно записать как 2А → В + С или А + D → P + Q В частном случае при с А = с D = с кинетическое уравнение для реакции второго порядка будет иметь вид:
В результате интегрирования получают уравнение для вычисления константы скорости реакции второго порядка Размерность k – л ∙ моль-1 ∙ с-1 или л ∙ моль-1 ∙ мин -1. Для реакций второго порядка линейная зависимость будет в координатах 1/с от t. Из уравнения (6.5) следует, что для реакции второго порядка то есть период полупревращения обратно пропорционален исходной концентрации. Следовательно, если для исследуемой реакции зависимость 1/с от времени линейна, и период полупревращения обратно пропорционален исходной концентрации, то это реакция второго порядка. Пример: Определим порядок и константу скорости реакции 2NO2 = 2NO + O2, если концентрация исходного вещества изменялась во времени следующим образом:
Решение: Константа скорости реакции не зависит от концентрации реагирующих веществ, поэтому эта величина не должна изменяться со временем. Используя экспериментальные данные и уравнения (6.4) и (6.5), рассчитаем константы скорости реакции в разные моменты времени. Результаты расчета приведены в таблице. Константа kI вычислена по уравнению (6.4), т.е. в предположении, что реакция 1-го порядка. Константа kII – по уравнению (6.5), т.е. предполагалось, что реакция 2-го порядка.
Как видно из результатов расчета, константа является постоянной величиной при вычислении по уравнению (6.5), т.е. реакция 2-го порядка. k ср = 6.27 л×моль-1×с-1. Графическая зависимость, построенная в координатах 1/с = f (t), будет линейной.
Зная величину константы скорости реакции, по уравнениям (6.4) и (6.5) легко вычислить концентрацию реагирующего вещества в любой момент времени. Это даст возможность рассчитать время, в течение которого следует проводить реакцию. Пример: Используя вычисленное значение константы скорости химической реакции (k ср = 6.27 л×моль-1×с-1) для реакции 2NO2 = 2NO + O2 , определим: 1. Время, за которое прореагирует 20% исходного вещества. Так как реакция 2-го порядка, то для расчета используем уравнение (6.5). Если прореагировало 20% от исходной концентрации, то концентрация вещества в искомый момент времени составит 0.8 с о. Тогда
2. Период полупревращения реакции. Для реакции 2-го порядка
3. Сколько прореагировало исходного вещества к моменту времени 1мин. Из уравнения (6.5)
Таким образом, концентрация исходного вещества к моменту времени 1 мин составила 3.59×10-3 моль×л-1. Следовательно, прореагировало Скорость гомогенной химической реакции, как правило, резко возрастает с ростом температуры. Иногда зависимость скорости реакции от температуры характеризуют величиной температурного коэффициента γ (температурный коэффициент Вант-Гоффа), который показывает, во сколько раз возрастает скорость химической реакции (константа скорости) при увеличении температуры на 10 градусов: где υ и kT – скорость и константа скорости реакции при температуре Т; υT +10 и kT +10 – скорость и константа скорости реакции при температуре Т +10. Обычно γ = 2 ÷ 4. Если температура возрастает больше, чем на десять градусов, то Пример: Константа скорости реакции димеризации бутадиена в газовой фазе при Т 1=503К равна 5.31×10-4 л×моль-1×с-1, а при Т 2=540К составляет 2.43×10--3 л×моль-1×с-1. Определим температурный коэффициент Вант-Гоффа и рассчитаем во сколько раз увеличивается скорость реакции при увеличении температуры на 15 градусов. Решение: Константы скорости реакции определены при температурах, отличающихся на
При увеличении температуры на Аррениус предположил, что уравнение для зависимости константы скорости реакции от температуры аналогично уравнению изобары химической реакции: где E a – энергия активации реакции Энергия активации - та минимальная энергия, которой должны обладать реагирующие частицы, чтобы при их столкновении могла бы произойти химическая реакция. Таким образом, Аррениусом впервые было введено представление о том, что не всякое столкновение частиц приводит к возникновению химической реакции, а только столкновение активных частиц, обладающих энергией активации Еа. Обычно считают, что Еа не зависит от температуры. Однако очень точные измерения показывают, что это справедливо лишь в первом приближении. Если в данном температурном интервале Еа = const, то, интегрируя уравнение (6.8), получим: где А – предэкспоненциальный множитель (предэкспонента). Численное значение этого коэффициента может быть рассчитано из теории элементарного акта химической реакции. Как правило, А слабо зависит от температуры. Тогда в первом приближении можно считать, что зависимость ln k от 1/ Т линейная, и величину энергии активации можно определить как тангенс угла наклона экспериментальной зависимости ln k = f (1/ Т): Энергию активации можно также определить, зная константы скорости при двух температурах: Пример: Для реакции С2Н2 +Н2 = С2Н4 при Т 1= 773К константа скорости k 1 = 1,14×10–2 (л×моль–1ּс–1), а при Т 2 = 825К значение k 2 = 7,11×10–2 (л×моль–1ּс–1). Определить энергию активации, предэкспоненциальный множитель А и константу скорости химической реакции при Т = 800К. Решение. Из уравнения (7.11) следует, что
Используя уравнение (6.9), получим ln А = ln k 1 + Ea / RT 1 = ln 1,14ּ10–2 + 186500 / (8,31 ּ 773) = 24,56 или А = 4,6×1010 л×моль–1ּс–1. Тогда при Т = 800 К ln k = ln А – Ea / RT = 24,56 – 186500 / (8,31 ּ 800) = – 3,49 или k = 3.04× 10–2 л×моль–1ּс–1. 6.1 Многовариантное задание № 14 «Расчет кинетических параметров гомогенных химических реакций»
Используя экспериментальные данные по изменению концентрации исходного вещества во времени для реакции В, заданной в таблице 6.1, выполните следующие действия: 1. Постройте графики зависимости концентрации с исходного вещества от времени t в координатах ln с = f (t) и 1 /с = f (t). По виду графика определите порядок реакции. 2. Рассчитайте константу скорости реакции В. 3. Вычислите концентрацию исходного вещества и продуктов реакции В через t 1 с от начала реакции. 4. Рассчитайте время, за которое прореагирует 10% исходного вещества. 5. Определите период полупревращения реакции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.13 (0.016 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

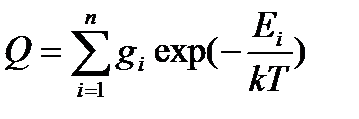
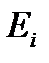 может отвечать несколько микросостояний. Число таких микросостояний
может отвечать несколько микросостояний. Число таких микросостояний 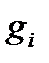 называется статистическим весом, а сами состояния – вырожденными.
называется статистическим весом, а сами состояния – вырожденными.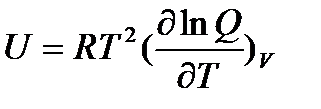
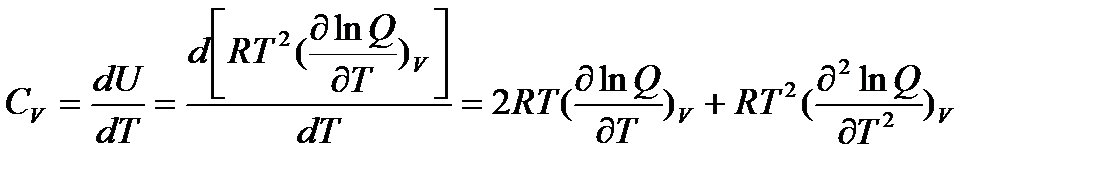
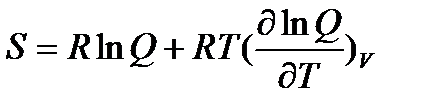
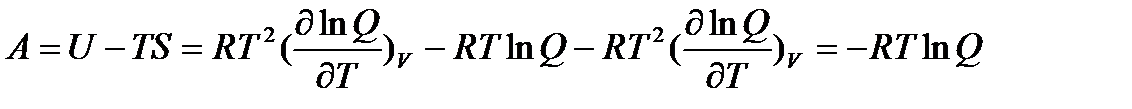
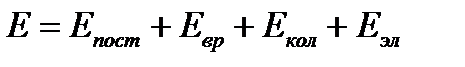
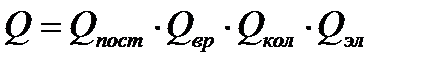
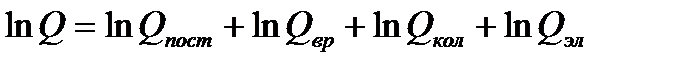
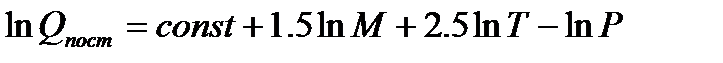 (5.7)
(5.7)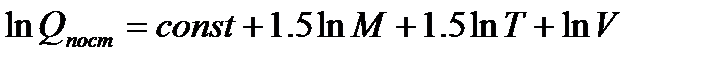
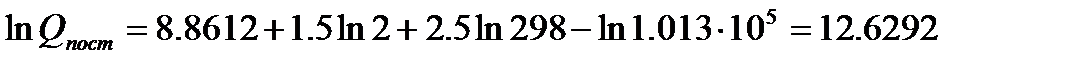
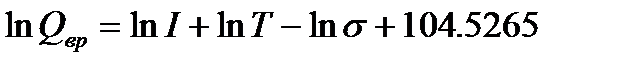 (5.8)
(5.8)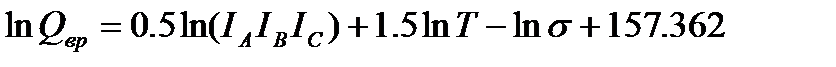 (5.9)
(5.9)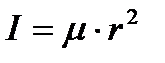 ,
,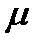 - приведенная масса.
- приведенная масса.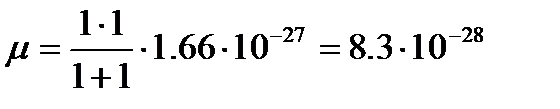 кг
кг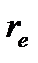 =0.741×10-10м (см.[2], табл. 107, с.177), следовательно, момент инерции равен
=0.741×10-10м (см.[2], табл. 107, с.177), следовательно, момент инерции равен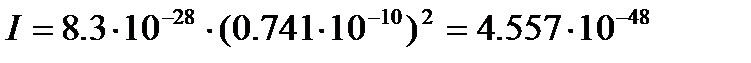 кг×м2
кг×м2 =2. И тогда
=2. И тогда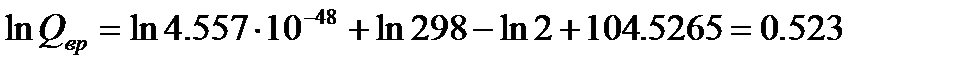
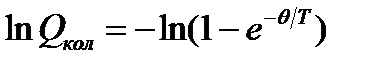 , (5.10)
, (5.10)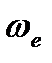
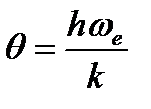
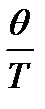 ([2], табл. 46, с.93).
([2], табл. 46, с.93).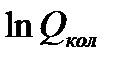 рассчитываются для одного конкретного колебания. Линейная многоатомная молекула, содержащая n атомов, обладает 3n-5 колебательными степенями свободы движения, а нелинейная имеет 3n-6 степеней свободы. Поэтому в многоатомных молекулах колебательные составляющие термодинамических функций, рассчитанные для каждого вида колебательного движения, суммируются.
рассчитываются для одного конкретного колебания. Линейная многоатомная молекула, содержащая n атомов, обладает 3n-5 колебательными степенями свободы движения, а нелинейная имеет 3n-6 степеней свободы. Поэтому в многоатомных молекулах колебательные составляющие термодинамических функций, рассчитанные для каждого вида колебательного движения, суммируются.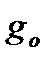 :
: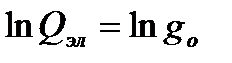 (5.11)
(5.11) 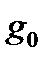 зависит от числа неспаренных электронов, находящихся на молекулярных орбиталях. Если все электроны спарены (синглетное состояние), то
зависит от числа неспаренных электронов, находящихся на молекулярных орбиталях. Если все электроны спарены (синглетное состояние), то 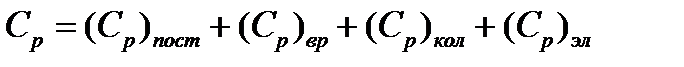 (5.12)
(5.12)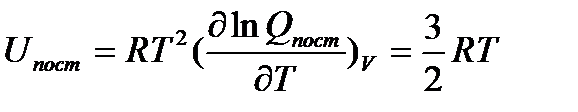 (5.13)
(5.13)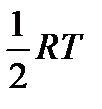 .
.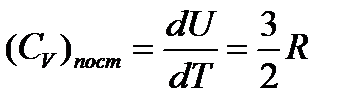 , а изобарная
, а изобарная 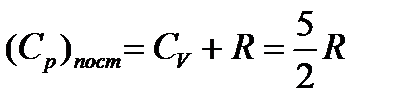 .
.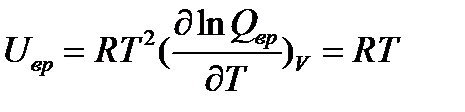 (5.14)
(5.14)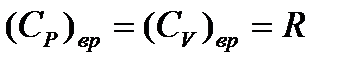 .
.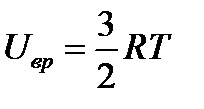 и
и 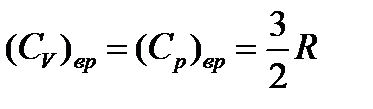 .
.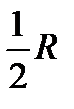 . Вращающиеся линейные молекулы имеют две степени свободы (координаты), а нелинейные молекулы – три степени свободы.
. Вращающиеся линейные молекулы имеют две степени свободы (координаты), а нелинейные молекулы – три степени свободы.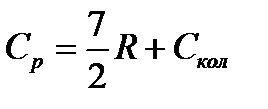 (5.15)
(5.15)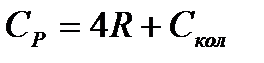 (5.16)
(5.16)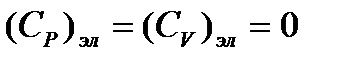 .
.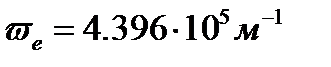 ([2], табл.107, с. 177) и
([2], табл.107, с. 177) и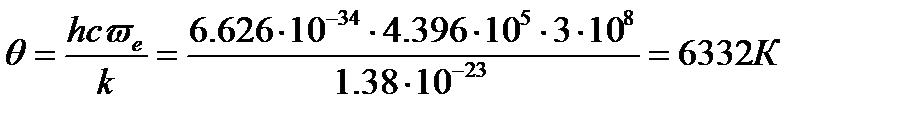
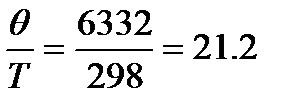
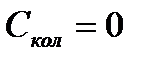 Дж/моль×К
Дж/моль×К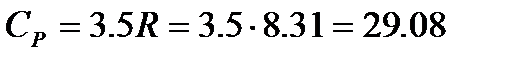 Дж/моль×К
Дж/моль×К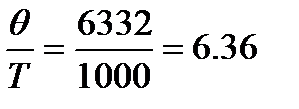
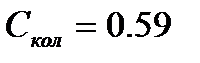 Дж/моль×К и
Дж/моль×К и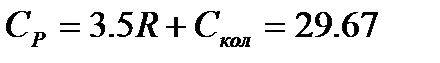 Дж/моль×К.
Дж/моль×К.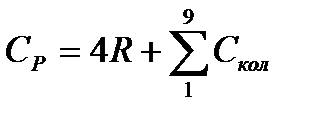
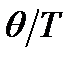
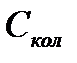
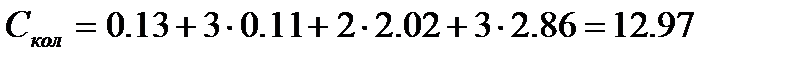 Дж/моль×К и изобарная молярная теплоемкость при 500К
Дж/моль×К и изобарная молярная теплоемкость при 500К 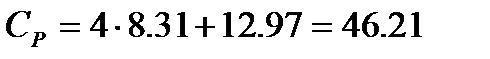 Дж/моль×К.
Дж/моль×К.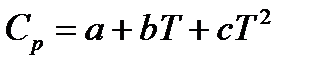 или
или 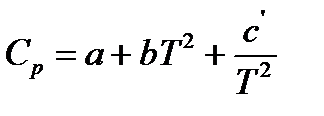 ,
,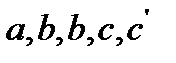 находятся из опытных данных и приводятся в справочниках (например, [2], табл. 44, с.72).
находятся из опытных данных и приводятся в справочниках (например, [2], табл. 44, с.72).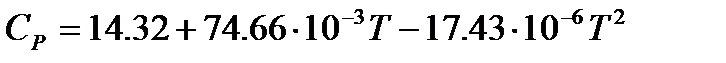 при 500К дает величину
при 500К дает величину 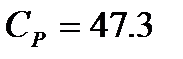 Дж/моль×К.
Дж/моль×К.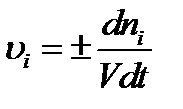 , (6.1)
, (6.1)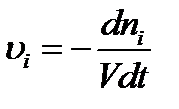 .
.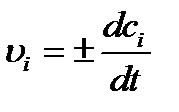 , (6.2)
, (6.2)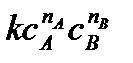 (6.3)
(6.3)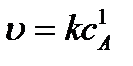 или
или 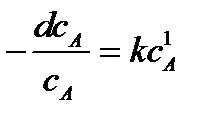
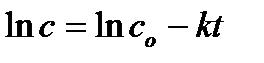 или
или 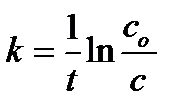 (6.4)
(6.4)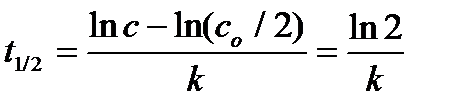
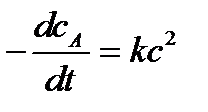 .
.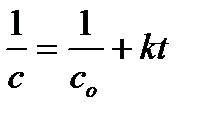 или
или 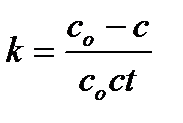 (6.5)
(6.5) 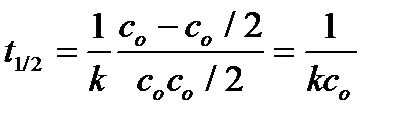 ,
, 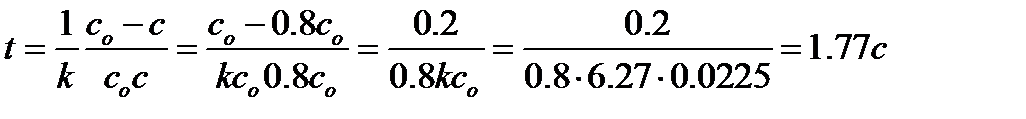
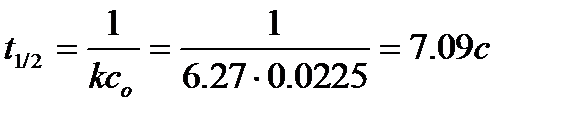
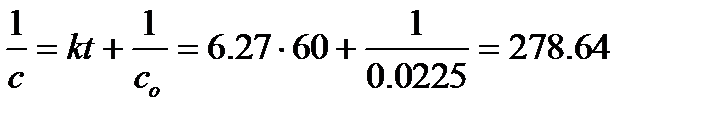 и с = 3.59×10-3 моль×л-1.
и с = 3.59×10-3 моль×л-1.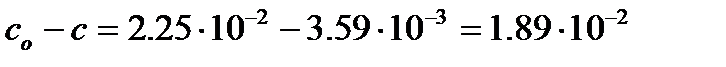 моль×л-1, т.е. 84 % от исходной концентрации.
моль×л-1, т.е. 84 % от исходной концентрации.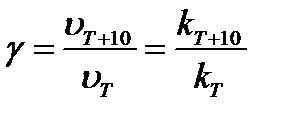 , (6.6)
, (6.6)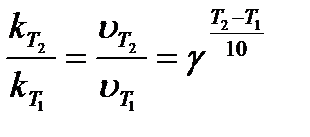 (6.7)
(6.7)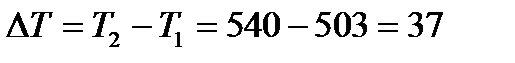 . Следовательно
. Следовательно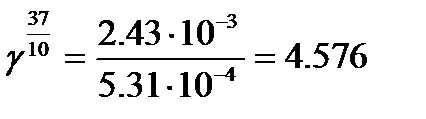 . Тогда
. Тогда 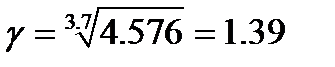 .
.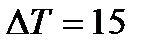 скорость реакции возрастет в
скорость реакции возрастет в 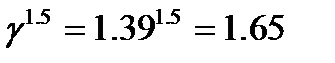 раз.
раз.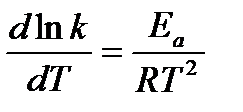 , (6.8)
, (6.8)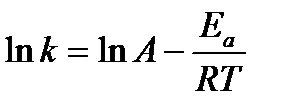 или k = А exp(– Ea / RT), (6.9)
или k = А exp(– Ea / RT), (6.9)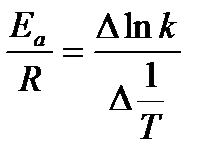 (6.10)
(6.10) 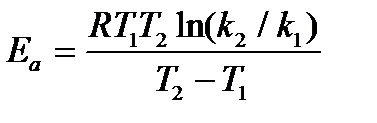 (6.11)
(6.11)