
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательные спектры двухатомных молекул
При сообщении молекуле достаточно высокой энергии ядра в молекуле начинают колебаться относительно положения равновесия. Если многоатомную молекулу, которую можно представить в виде материальных точек, в которых сосредоточены массы атомов, соединенных пружинками, раскачать, то она будет совершать сложное движение, так называемое движение Лиссажу. Такое движение можно разложить на сравнительно небольшое число нормальных колебаний, при которых все ядра колеблются в одной фазе и с одной частотой, и которое можно описать набором нормальных координат. Число нормальных колебаний (или колебательных степеней свободы) молекулы, состоящей из N атомов, может быть рассчитано как 3N − 5 для линейных молекул и 3N − 6 для нелинейных молекул. При этом расчете из общего числа степеней свободы N-атомной молекулы, равного 3N, вычитаются три степени свободы поступательного движения молекулы как целого и две (для линейной) или три (для нелинейной) степени свободы вращательного движения. Например, для двухатомной молекулы число колебательных степеней свободы равно 3 ∙ 2 − 5 = 1. Это валентное колебание, связанное с изменением длины связи.
Рисунок 4.7 – Валентное колебание на примере молекулы HCl
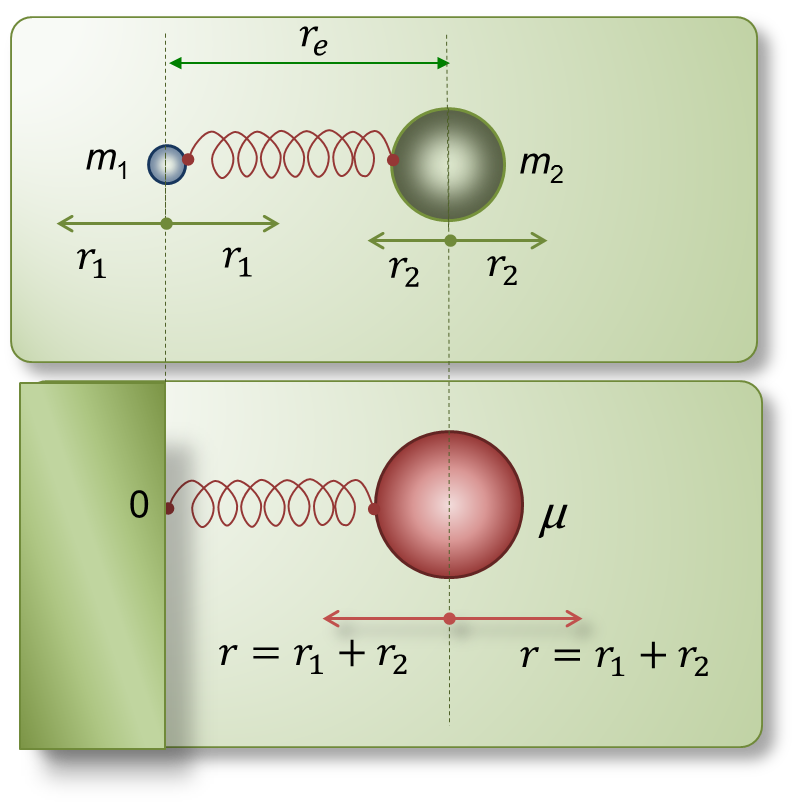
В трехатомной линейной молекуле типа XY2 (например, CO2) число нормальных колебаний равно 3 ∙ 3 − 5 = 4. Для такой молекулы кроме двух валентных (симметричного ν s и ассиметричного ν as) есть еще два деформационных колебания δ, связанных с изменением валентного угла в молекуле в двух взаимно перпендикулярных плоскостях. Простейшей моделью двухатомной колеблющейся молекулы является гармонический осциллятор - система из двух шариков, связанных пружинкой и колеблющихся с постоянной частотой (рисунок 4.8). Колебания в такой молекуле можно рассматривать как происходящие с той же частотой колебания массы, равной приведенной массе молекулы, относительно неподвижной стенки, к которой она присоединена той же пружинкой.
Рисунок 4.8 – Модель гармонического осциллятора
Частота колебаний гармонического осциллятора зависит от силы упругости
где k – коэффициент упругости (силовая постоянная).
Потенциальная энергия такой системы:
Данная зависимость отвечает уравнению параболы. Подставив потенциальную энергию в уравнение Шредингера и решив его, можно получить уравнение для энергии гармонического осциллятора
где
где Колебательное квантовое число может принимать значения Правило отбора для модели гармонического осциллятора Энергия нулевого колебательного уровня в модели гармонического осциллятора:
Из уравнения (4.58) следует, что энергия нулевого колебательного уровня отлична от нуля, что свидетельствует о том, что даже при абсолютном нуле остаются, хотя и незначительные, колебания, и имеется вероятность найти частицы в положении, отличном от равновесия. Зависимость потенциальной энергии гармонического осциллятора имеет вид параболы (рисунок 4.9 а). Расстояние между соседними уровнями колебательной энергии является постоянной величиной, равной
Колебательный спектр гармонического осциллятора представляет собой одну линию с волновым числом, равным волновому числу собственных колебаний (рисунок 4.9 б):
Реальная молекула отличается от гармонического осциллятора, поскольку входящие в нее атомы при сообщении молекуле достаточно большой энергии могут быть удалены друг от друга сколь угодно далеко вплоть до разрыва связи. Напротив, сближению атомов мешают силы отталкивания. В связи с этим потенциальная кривая реальной молекулы отличается от параболы (рисунки 4.10 и 4.11 а).
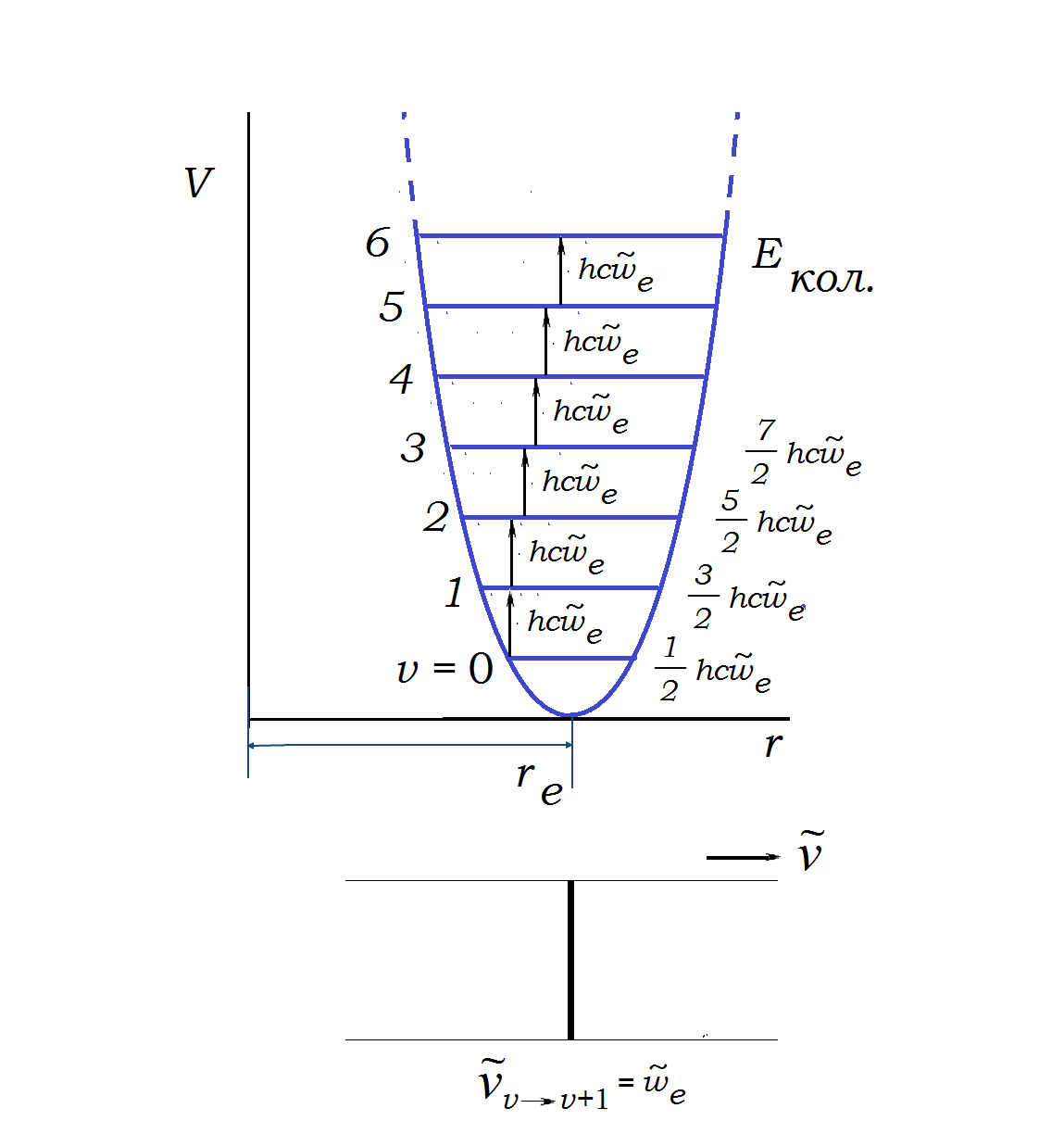
Рисунок 4.9 – Кривая потенциальной энергии гармонического осциллятора (а) и схематичный вид колебательного спектра (б)
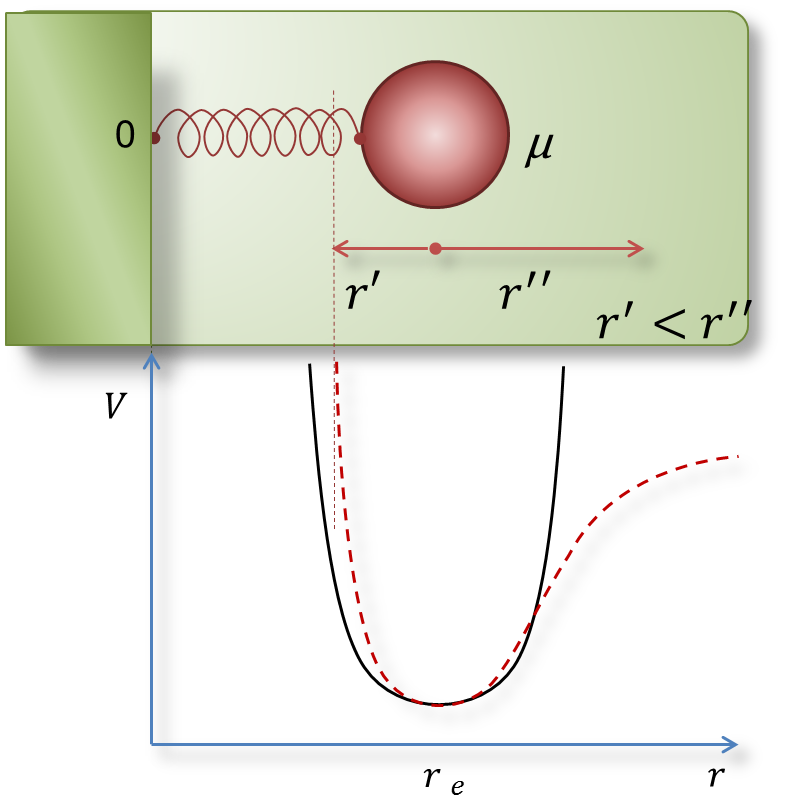
Рисунок 4.10 – Модель ангармонического осциллятора (а) и зависимость потенциальной энергии молекулы (б) (сплошная линия – гармонический осциллятор, штриховая – ангармонический осциллятор)
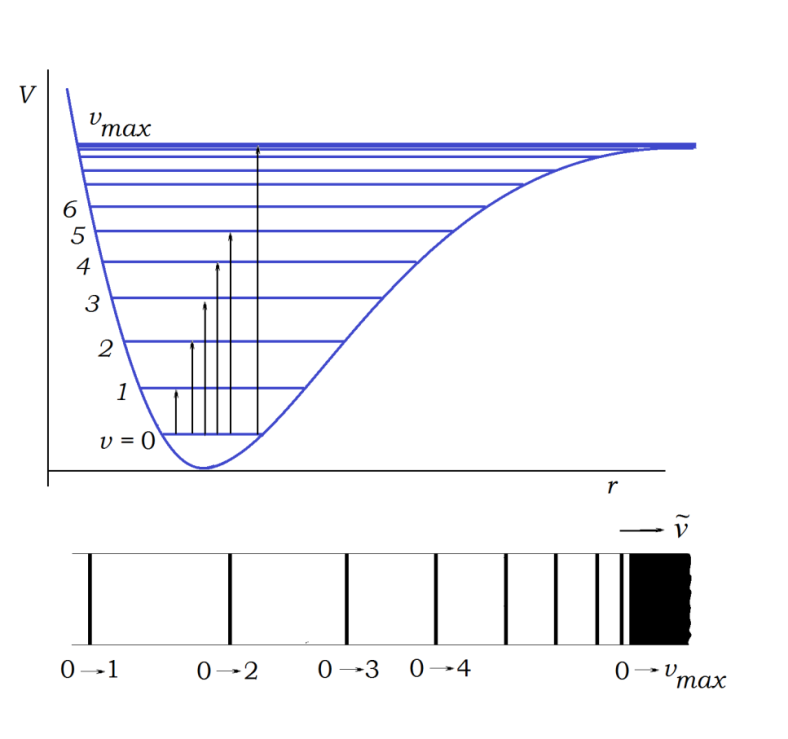
Рисунок 4.11 – Кривая потенциальной энергии ангармонического осциллятора (а) и схематичный вид колебательного спектра (б)
В результате подстановки в уравнение Шредингера уравнения потенциальной энергии Морзе
где
получаем уравнение для колебательной энергии ангармонического осциллятора:
где Колебательное квантовое число может принимать значения:
Правило отбора для колебательных переходов:
Приняты обозначения. Поглощение кванта света, приводящее к переходу молекулы с нулевого на первый колебательный уровень, приводит к появлению линии в спектре, называемой основным тоном, но второй – первым обертоном, на третий – вторым обертоном и т.д. (рисунок 4.11 б). Расстояния между линиями в колебательном спектре молекулы при увеличении волнового числа закономерно уменьшаются. Поскольку большинство молекул при невысоких температурах находятся на нулевом колебательном уровне, то в спектре проявляются переходы с этого уровня. Лишь при существенном увеличении температуры в спектре могут быть обнаружены так называемые «горячие» частоты, отвечающие переходам молекулы с более высоких уровней энергии. Энергию нулевого колебательного уровня в модели ангармонического осциллятора можно рассчитать по уравнению:
Изменение колебательной энергии при переходе с нулевого колебательного уровня на любой уровень
а волновое число отвечающей этому переходу линии в спектре по уравнению (4.65):
Анализ схематичного изображения кривой потенциальной энергии и колебательного спектра ангармонического осциллятора на примере двухатомной молекулы (рисунок 4.11) свидетельствует о том, что с ростом колебательного квантового числа
Рисунок 4.12 – Определение энергии диссоциации энергии ангармонического осциллятора
Для нахождения значения максимального колебательного квантового числа можно использовать граничные условия:
или
Подстановка в первое граничное условие выражения для колебательной энергии ангармонического осциллятора (уравнение (4.62)) приводит к формуле расчета максимального колебательного квантового числа:
Подстановка полученного выражения в уравнение (4.62) дает возможность рассчитать энергию максимального колебательного уровня:
и далее энергию диссоциации:
По второму граничному условию получается иное уравнение для энергии диссоциации, дающее, однако, близкие расчетные результаты:
Домножение энергии диссоциации на число Авогадро в уравнениях (4.71) и (4.72) позволяет выразить энергию в кДж/моль.
В колебательных спектрах также можно заметить изотопный сдвиг. Оценить его величину можно из отношения волновых чисел собственных колебаний неизотопной и изотопозамещенной молекул, записанных по уравнению (4.57):
Если силовые постоянные близки
Пример: Составьте уравнения для расчета волнового числа линий в спектре, отвечающих переходу с нулевого уровня энергии на первый (основной тон), на второй (первый обертон), на третий (второй обертон).
Решение. Подставим в уравнение (4.65) для основного тона
для первого обертона
для второго обертона
Пример: В инфракрасном спектре поглощения двухатомной молекулы определены положения двух первых самых сильных линий 3962 и 7743 см-1. Найдите волновое число собственных колебаний, коэффициент ангармоничности и ангармоничность молекулы. Решение. Первая линия отвечает основному тону (уравнение (4.75)), вторая – первому обертону (уравнение (4.76)). Составим и решим систему уравнений:
Домножим первое уравнение на 3:
Вычтем из первого уравнения второе:
Подставим полученное значение, например, в первое уравнение (уравнение для основного тона) и вычислим ангармоничность и далее коэффициент ангармоничности:
Пример: В колебательном спектре молекулы CO в свободном состоянии и в случаях, когда CO адсорбирована на поверхности металлов определены волновые числа основной полосы поглощения. Волновое число собственных колебаниий CO в свободном неадсорбированном состоянии 2169 см-1. Считая коэффициент ангармоничности во всех случаях одним и тем же, рассчитайте волновые числа собственных колебаний CO, энергию и силовую постоянную связи C=O во всех случаях. Сделайте вывод о характере адсорбции.
Решение. Основной полосе CO или основному тону отвечает уравнение (4.75). Используем данные для молекулы CO в свободном состоянии
Преобразуем уравнение (4.75) относительно
Cu:
Pt:
Pd:
Ni:
Энергия связи в молекуле противоположна по физическому смыслу энергии диссоциации. Используем для ее оценки, например, уравнение (4.71):
CO:
или
Энергии диссоциации для молекул CO, адсорбированных на металлах, оцениваем аналогично: Cu: или Pt: или Pd: или Наконец, Ni: или Для нахождения силовой постоянной перепишем уравнение (4.57):
Вначале оценим приведенную массу молекулы CO:
Затем рассчитаем силовые постоянные:
для свободной CO:
и для адсорбированной на металлах молекулы CO:
Cu:
Pt:
Pd:
Ni:
Анализ выполненных вычислений свидетельствует об уменьшении энергии связи и силовой постоянной и, следовательно, об ослаблении связи С=O при адсорбции на металлах. Пример: Оцените величину и направление изотопного сдвига основной полосы поглощения в колебательном спектре молекулы 13CO, адсорбированной на поверхности меди.
Решение. Из предыдущего примера возьмем необходимые данные для неизотопозамещенной молекулы CO, адсорбированной на меди: волновое число собственных колебаний:
приведенная масса молекулы CO:
Рассчитаем приведенную массу изотопозамещенной молекулы 13CO:
Предполагая, что силовые постоянные близки
Положение полосы основного тона определим по уравнению (4.75), позаимствовав из предыдущего примера значение коэффициента ангармоничности и положение полосы основного тона для неизотопозамещенной молекулы CO, адсорбированной на меди:
Делаем вывод: изотопный сдвиг в длинноволновую (или низкочастотную) область составляет 2128 - 2082 = 46 см-1.
4.2.6 Многовариантное задание №12 «Колебательные спектры двухатомных молекул»
1. Напишите квантово-механическое уравнение для расчета энергии колебательного движения двухатомной молекулы как гармонического осциллятора. 2. Напишите квантово-механическое уравнение для расчета энергии колебательного движения двухатомной молекулы как ангармонического осциллятора. 3. Вычислите по определенным изИК-спектра поглощения двухатомной молекулы A основному тону ( 4. Вычислите волновые числа пропущенных линий в ИК-спектре поглощения двухатомной молекулы A ( 5. Определите энергию колебательного движения молекулы A на нулевом колебательном квантовом уровне E 0 (Дж), используя волновое число собственных колебаний
6. Выведите уравнение для расчета максимального колебательного квантового числа. 7. Определите максимальное колебательное квантовое число 8. Определите энергию колебательного движения 9. Определите энергию диссоциации D 0 молекулы A (кДж/моль). 10. Вычертите график зависимости 11. Укажите на графике энергию колебательного движения на максимальном колебательном квантовом уровне E max (Дж) и энергию диссоциации D 0 . 12. Вычислите силовую постоянную химической связи 13. Вычислите волновое число собственных колебаний изотопозамещенной молекулы B. 14. Определите величину и направление изотопного сдвига для основного тона.
Таблица 4.4 – Варианты заданий
Продолжение таблицы 4.4
Продолжение таблицы 4.4
Продолжение таблицы 4.4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.195.24 (0.138 с.) |
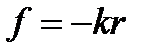 ,
,
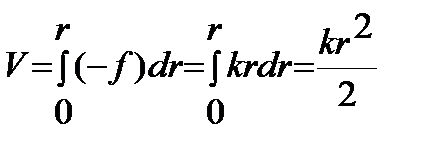
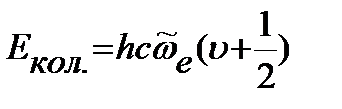 ,
,
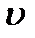 - колебательное квантовое число,
- колебательное квантовое число, 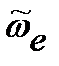 - волновое число «собственных» колебаний, связанное с упругой или силовой постоянной ke уравнением
- волновое число «собственных» колебаний, связанное с упругой или силовой постоянной ke уравнением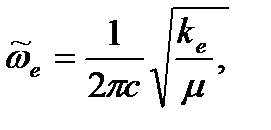
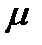 - приведенная масса.
- приведенная масса.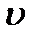 =0, 1, 2 …
=0, 1, 2 …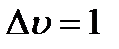 .
.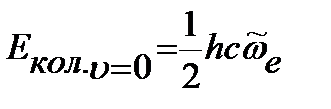 ,
,
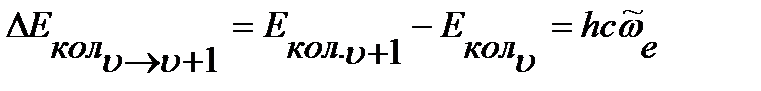 .
.
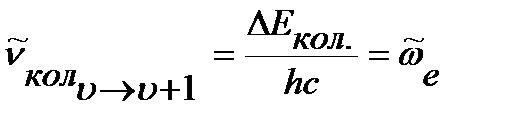 .
.
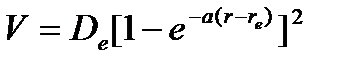
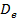 – глубина потенциальной ямы, а коэффициент
– глубина потенциальной ямы, а коэффициент 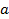 связан с волновым числом собственных колебаний уравнением
связан с волновым числом собственных колебаний уравнением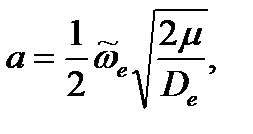
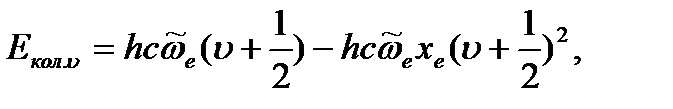
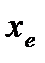 – коэффициент ангармоничности;
– коэффициент ангармоничности; 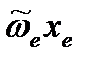 – ангармоничность.
– ангармоничность.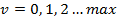
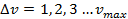
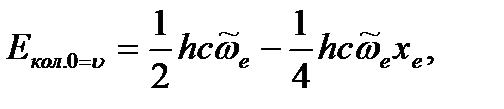
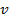 можно определить по уравнению (4.64):
можно определить по уравнению (4.64):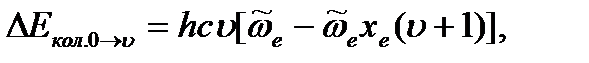
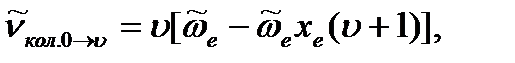
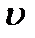 расстояния между уровнями энергии уменьшаются, а линии в спектре, соответствующие поглощению кванта при переходе на уровень
расстояния между уровнями энергии уменьшаются, а линии в спектре, соответствующие поглощению кванта при переходе на уровень 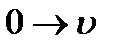 , сближаются. Последний переход
, сближаются. Последний переход 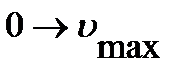 , отвечающий диссоциации молекулы на атомы, соответствует границе дискретного и сплошного спектра. Соотношение между энергией диссоциации
, отвечающий диссоциации молекулы на атомы, соответствует границе дискретного и сплошного спектра. Соотношение между энергией диссоциации 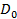 и глубиной потенциальной ямы
и глубиной потенциальной ямы 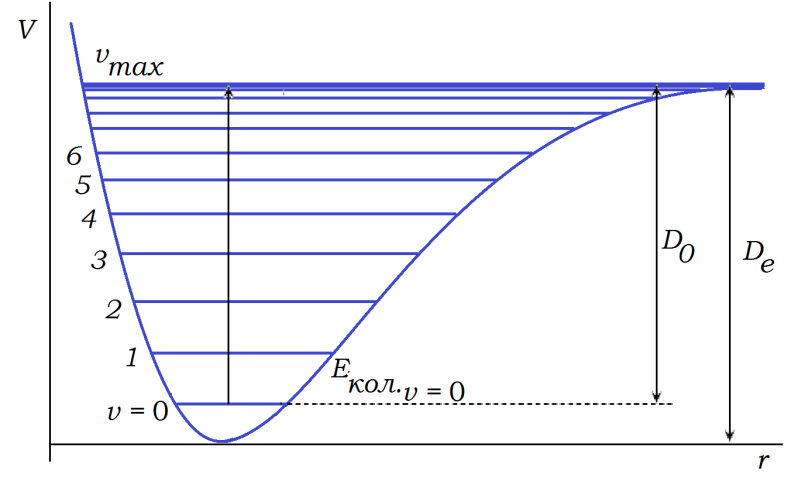
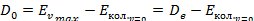
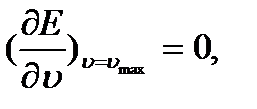
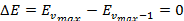
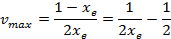
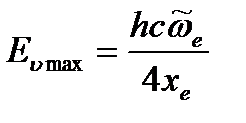
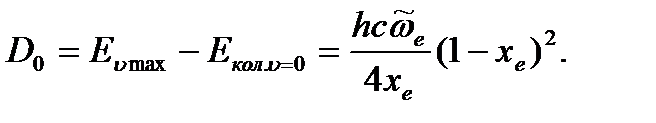
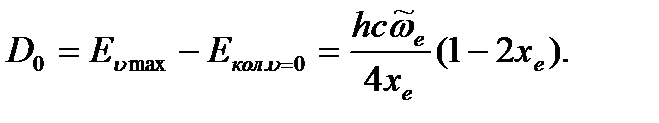
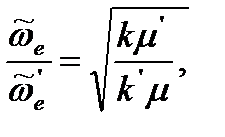
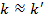 , то уравнение еще более упрощается:
, то уравнение еще более упрощается: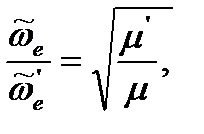
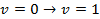
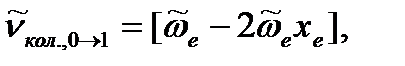
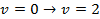
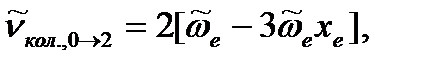
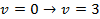
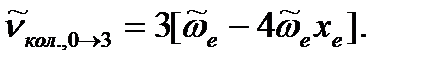
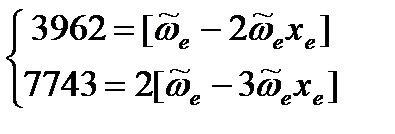
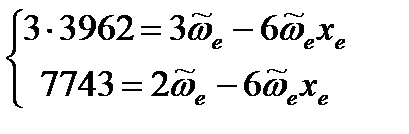

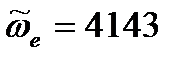 см-1
см-1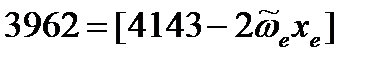
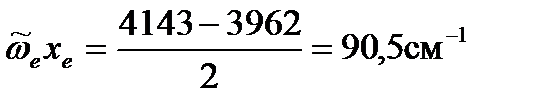
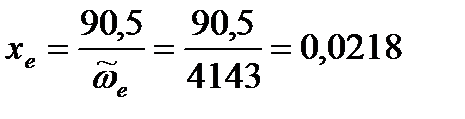
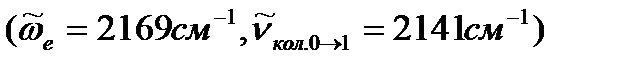 для нахождения коэффициента ангармоничности:
для нахождения коэффициента ангармоничности: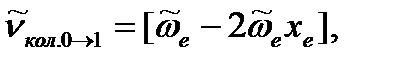
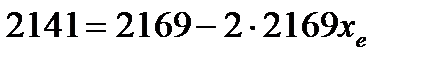
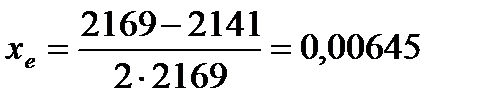
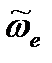 и рассчитаем волновые числа собственных колебаний для молекул CO, адсорбированных на металлах:
и рассчитаем волновые числа собственных колебаний для молекул CO, адсорбированных на металлах: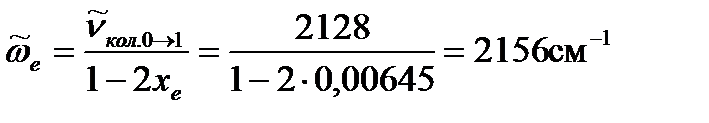
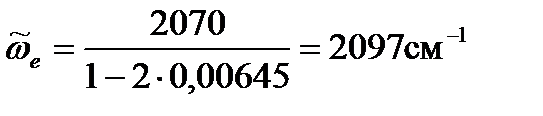
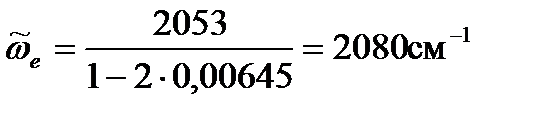
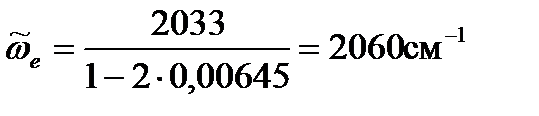
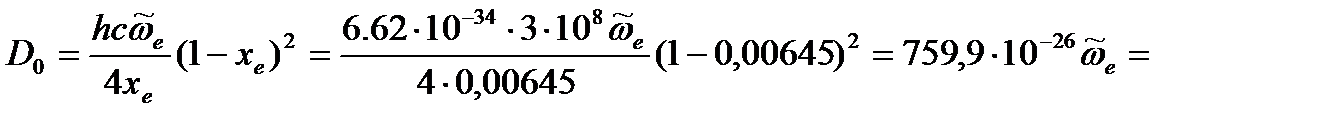
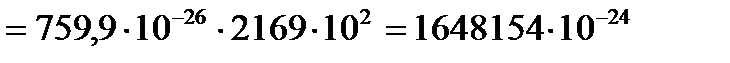 Дж
Дж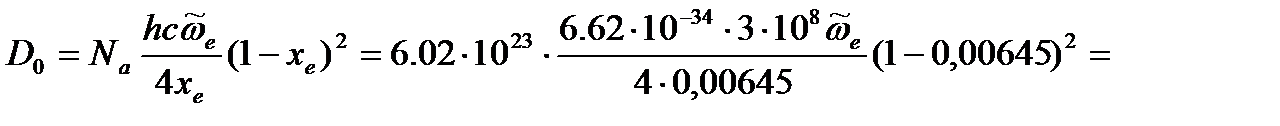
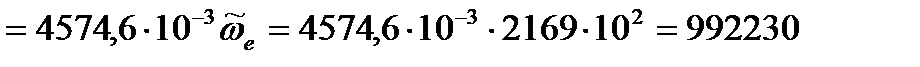 Дж/моль
Дж/моль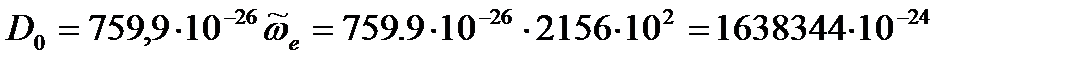 Дж
Дж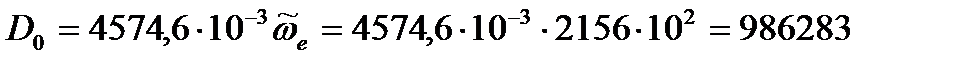 Дж/моль.
Дж/моль.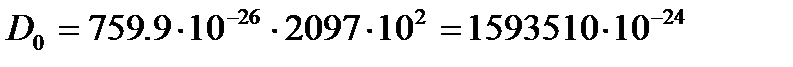 Дж
Дж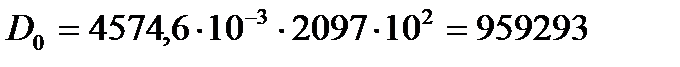 Дж/моль.
Дж/моль.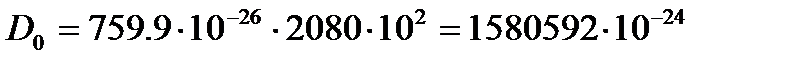 Дж
Дж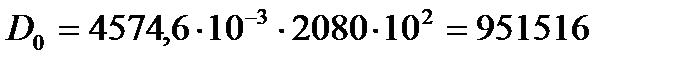 Дж/моль.
Дж/моль.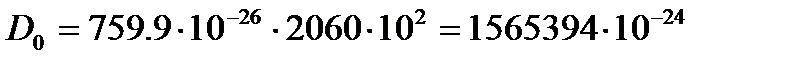 Дж
Дж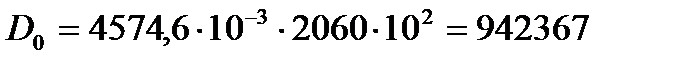 Дж/моль.
Дж/моль.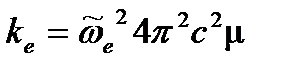
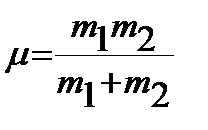 , где массы ядер углерода
, где массы ядер углерода 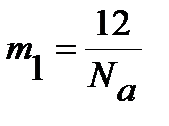 и кислорода
и кислорода 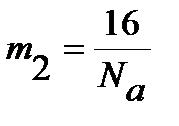 (в граммах).
(в граммах).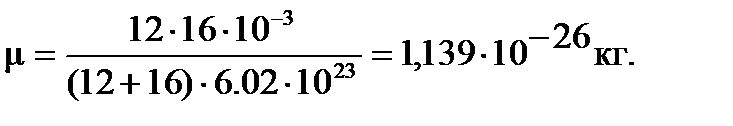
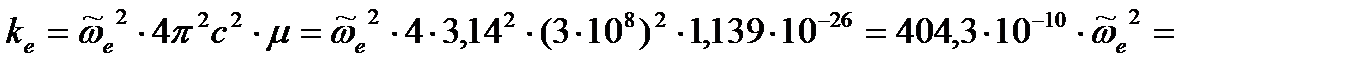
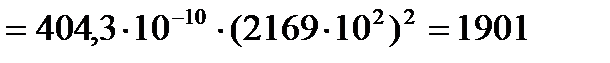 кг/с2
кг/с2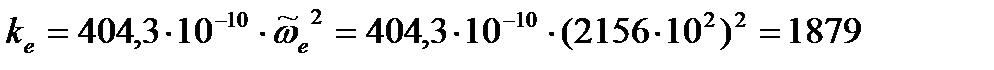 кг/с2
кг/с2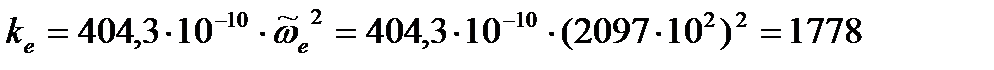 кг/с2
кг/с2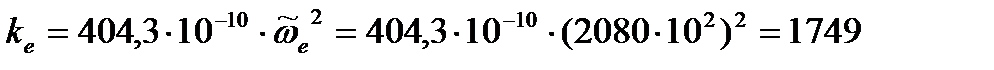 кг/с2
кг/с2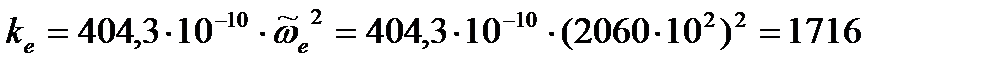 кг/с2
кг/с2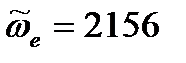 см-1,
см-1,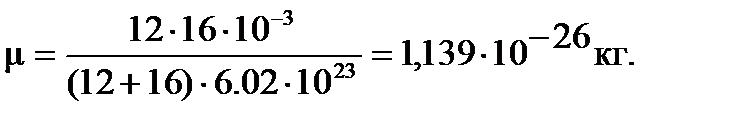
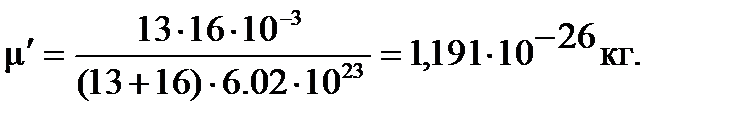
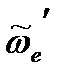 для изотопозамещенной молекулы:
для изотопозамещенной молекулы: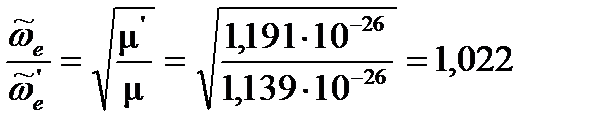
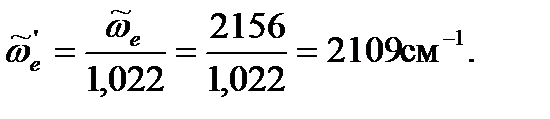
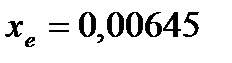
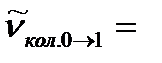 2128 см-1.
2128 см-1.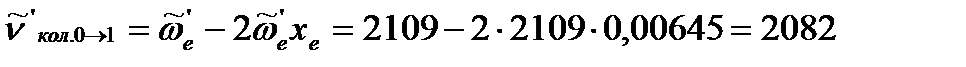 см-1.
см-1.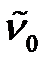 ), первому обертону (
), первому обертону (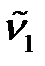 ), второму обертону (
), второму обертону (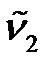 ) или третьему обертону (
) или третьему обертону (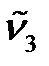 ) (таблица 4.4) волновое число собственных колебаний
) (таблица 4.4) волновое число собственных колебаний 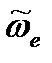 , коэффициент ангармоничности
, коэффициент ангармоничности 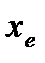 и ангармоничность
и ангармоничность 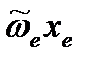 .
.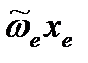 (см. п.3)
(см. п.3)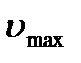 для молекулы A.
для молекулы A.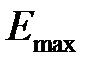 (Дж) на максимальном колебательном квантовом уровне.
(Дж) на максимальном колебательном квантовом уровне.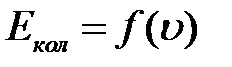 , выбрав 3-4 значения квантового числа
, выбрав 3-4 значения квантового числа 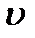 и рассчитав значения E кол. в интервале от 0 до
и рассчитав значения E кол. в интервале от 0 до 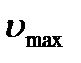 .
.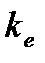 двухатомной молекулы A.
двухатомной молекулы A.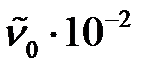 , м-1
, м-1
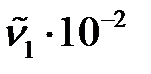 , м-1
, м-1
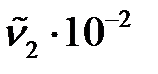 , м-1
, м-1
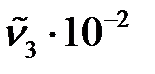 , м-1
, м-1



