
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Константы равновесия гетерогенных реакций
Гетерогенные реакции – это реакции, в которых реагирующие вещества находятся в разных фазах. В выражения для констант равновесия гетерогенных реакций входят концентрации (парциальные давления или количества вещества) только газообразных или растворенных веществ. Например, для реакции
S(тв) + О2(г) = SO2(г)
константа равновесия, выраженная через приведенные давления
Для реакции
S2(г) + Fe(тв) = FeS(тв)
Пример: Определим равновесные парциальные давления газообразных веществ при температуре 800 К и нормальном атмосферном давлении в реакции
WO3 + 3H2 = W + 3H2O,
если константа равновесия реакции при температуре 800 К и атмосферном давлении Решение: Запишем выражение для константы равновесия химической реакции через приведенные парциальные давления газообразных веществ
Так как в уравнении два неизвестных, запишем второе уравнение:
Решая систему уравнений получим:
или
Откуда
Парциальные давления газообразных веществ при нормальном атмосферном давлении равны:
1.9 Многовариантное задание №1 «Расчет степени превращения, равновесного состава и выхода продукта химической реакции и выбор оптимальных условий проведения процесса»
Для выполнения этого задания предлагается следующий алгоритм: 1. На основании значений теплот образования веществ 2. Определите изменение числа молей газообразных веществ реакции А при 298К и стандартном давлении. 3. Рассчитайте работу (в кДж), совершаемую в реакции А против внешнего давления при p = const и T = 298 K. 4. Определите изохорный тепловой эффект химической реакции А QV = 5. На основании данных из справочника [2] определите изменение средней теплоемкости в системе в результате реакции А 6. Определите тепловой эффект реакции А при температуре T и стандартном давлении
7. Установите, как будет меняться тепловой эффект химической реакции А при повышении температуры. Ответ аргументируйте, используя соответствующие уравнения химической термодинамики. 8. Определите изменение энтропии системы (в Дж/К) в результате химической реакции А (таблице 1.1), протекающей между веществами в идеальном газообразном состоянии при стандартном давлении и температуре 298 К. Значения стандартной энтропии для веществ возьмите из справочника [2]. 9. Рассчитайте изменение энтропии 10. Определите изменение стандартной энергии Гиббса 11. Рассчитайте термодинамическую константу равновесия Ka реакции А при температуре 298 К и температуре Т. 12. Определите глубину превращения ξ в реакции A при температуре Т и атмосферном давлении при условии, что исходные вещества взяты в стехиометрических количествах. 13. Определите глубину превращения ξ в реакции A при температуре Т и атмосферном давлении при условии, что исходные вещества взяты в количествах, указанных в таблице 1.2. 14. Определите степень превращения исходных веществ при условиях 12 и 13. 15. Определите состав равновесной смеси в %(мол.) для химической реакции А при температуре Т и атмосферном давлении при условиях 1.12 и 1.13. 16. Установите, как влияет повышение температуры на термодинамическую константу равновесия Ka и равновесный выход продуктов химической реакции А. Ответ аргументируйте, используя соответствующие уравнения химической термодинамики. Сопоставьте сделанные выводы с расчетными значениями констант равновесия. 17. Установите, как влияет повышение общего давления на равновесный выход продуктов химической реакции А. Ответ аргументируйте.
Таблица 1.1 – Варианты заданий
Таблица 1.2 – Варианты заданий
1.10 Многовариантное задание №2 «Расчет равновесных парциальных давлений гетерогенной химической реакции»
1. Определите константу равновесия Ka химической реакции В при температуре T с использованием средних изобарных теплоемкостей. 2. Запишите в общем виде выражение для константы равновесия химической реакции B через парциальные давления реагирующих веществ. 3. Определите парциальные давления газообразных веществ при температуре T и атмосферном давлении. 4. Оцените влияние изменения общего давления, температуры и разбавления реакционной смеси газом, не участвующим в химической реакции, на положение равновесия реакции и равновесный выход продукта.
Таблица 1.3 – Варианты заданий
1.11 Контрольные вопросы
1. По изменению каких термодинамических функций рассчитывается тепловой эффект химической реакции, протекающей в изобарных или изохорных условиях? 2. Как формулируется закон Гесса? 3. Какие следствия из закона Гесса Вы знаете? 4. Что называется стандартной теплотой образования вещества? 5. Как рассчитывается тепловой эффект реакции с использованием теплот образования? 6. Как рассчитывается тепловой эффект реакции с использованием теплот сгорания? 7. Что называется стандартной теплотой сгорания вещества? 8. Что такое истинная и средняя молярная изобарная теплоемкость? 9. Как формулируется закон Кирхгоффа в дифференциальной и интегральной форме? 10. Как зависит тепловой эффект химической реакции от температуры? Ответ подтвердите соответствующим уравнением. 11. Почему в справочниках приводятся абсолютные значения энтропии веществ, а абсолютные значения энтальпии – нет? 12. Какие критерии направления процессов в изолированных и закрытых системах Вы знаете? 13. Что является критерием равновесия в закрытых системах? 14. Что такое термодинамические и практические константы равновесия химических реакций? Приведите примеры. 15. С помощью какого уравнения рассчитываются термодинамические константы равновесия? 16. Что такое химическая переменная (глубина превращения в химической реакции)? Как эта величина используется для расчета равновесного состава в химическом процессе? 17. Что такое степень превращения исходных веществ в химической реакции? 18. Как влияет температура на равновесный выход продукта химической реакции? Ответ подтвердите соответствующим уравнением. 19. Как влияет давление на равновесный выход продукта химической реакции? Ответ подтвердите соответствующим уравнением. 20. В чем особенность расчета равновесного состава газовой смеси в гетерогенной реакции?
ФАЗОВЫЕ РАВНОВЕСИЯ Основными понятиями в теории фазовых равновесий являются: система, фаза, компоненты, термодинамические степени свободы, вариантность системы.
Фаза – совокупность однородных частей системы, отделенная от других частей системы границей (поверхностью) раздела и имеющая в каждой точке одинаковые химические и физические свойства. Фаза характеризуется уравнением состояния. Гомогенная система – однородная система, состоящая из одной фазы. Гетерогенная система – неоднородная система, состоящая из нескольких фаз. Составляющие вещества – вещества, которые могут быть выделены из системы и вне нее могут устойчиво существовать. Компоненты системы – составляющие вещества, наименьшее число которых достаточно для образования системы. Если в системе не происходит химических взаимодействий, то число компонентов равно числу составляющих веществ. А если в системе происходит химическое взаимодействие, то число компонентов меньше числа составляющих веществ на число уравнений, связывающих концентрации этих веществ. Термодинамические степени свободы – число параметров, определяющих состояние системы, которые можно менять произвольно и независимо друг от друга, не вызывая при этом изменения числа и природы фаз в системе. В качестве таких параметров, как правило, выбирают давление, температуру и концентрации. Вариантность системы – число термодинамических степеней свободы. Условием равновесия в системе в изобарно-изотермических условиях (при p = const и T = const) является выполнение следующих равенств:
или
где k – число компонентов в системе.
Если в равновесии находятся две фазы
то
откуда
В многофазной гетерогенной системе условием равновесного существования фаз является равенство химических потенциалов для каждого i -го компонента во всех фазах:
где f – число фаз в системе. Правило фаз Гиббса, которое называют также основным законом фазовых равновесий, устанавливает связь между числом компонентов k, числом фаз f и числом термодинамических степеней свободы (вариантностью) s и выражается уравнением:
где n – число параметров (температура и давление), определяющих состояние системы. Если, кроме концентраций, параметрами, определяющими состояние системы, являются только давление и температура, то n = 2. В частных случаях, когда один из параметров поддерживается неизменным, например, давление (в изобарных условиях) или температура (в изотермических условиях), n = 1. В изобарно-изотермических условиях (когда p = const и T = const) n = 0. Если в равновесной системе число термодинамических степеней свободы s = 2, то она называется бивариантной. Это означает, что произвольным образом и независимо друг от друга, не вызывая изменения фазового состава системы можно менять два параметра состояния. Когда s = 1, система называется моновариантной и произвольным образом можно изменять только один параметр. При s = 0 ни один из параметров состояния не может изменяться, не вызывая изменения фазового состава. В этом случае систему называют нонвариантной или безвариантной.
Однокомпонентные системы В зависимости от условий в однокомпонентной системе – индивидуальном веществе – могут сосуществовать одна, две или три устойчивые фазы. Например, при определенных условиях в воде могут находиться в равновесии жидкая вода и газообразная вода (водяной пар) или лед, жидкая вода и пары воды. В однокомпонентной системе, состояние которой определяется двумя параметрами – давлением и температурой – число фаз в равновесии не может быть больше 3. Покажем это с помощью правила фаз Гиббса при k = 1:
Откуда
Максимальное число фаз получим при s = 0, следовательно, в однокомпонентной системе
Фазовые равновесия в однокомпонентной системе описываются уравнением Клаузиуса, которое в дифференциальной форме имеет вид
Оно связывает производную давления насыщенного пара вещества по температуре Уравнение Клапейрона (2.6) является универсальным уравнением, применимым к любому двухфазному равновесию. Рассмотрим применение уравнения Клапейрона к различным фазовым переходам, имеющим практическое значение. Плавление – это переход вещества из твердого состояния в жидкое. В этом случае уравнение Клапейрона используют для анализа влияния давления на температуру плавления, поэтому его записывают в виде:
где Характер изменения температуры плавления от давления определяется знаком производной Однако, имеется небольшое число веществ (вода, висмут, галлий), для которых наблюдается иная (аномальная) зависимость температуры плавления от давления. У этих веществ при плавлении происходит уменьшение объема, а при кристаллизации – увеличение. Всем хорошо известно, что при замерзании воды ее объем увеличивается настолько, что в замкнутой системе происходит разрыв даже стальных и чугунных труб. Для этих веществ Δ fus V < 0 и, следовательно, Испарение – это процесс перехода из жидкого состояния в газообразное. Газ, полученный испарением жидкости, называют паром. Изменение молярного объема при испарении представляет собой разность между объемом 1 моля вещества в газоообразном (Vg) и в жидком состоянии(Vl): Δ vap V = Vg – Vl,
здесь vap – сокращение от английского слова vaporization – испарение. В одинаковых условиях молярный объем любого вещества в газообразном состоянии во много раз больше, чем объем 1 моля в жидком виде. Например, объем 1 моля воды в газообразном состоянии при температуре кипения (373 К) и стандартном давлении (101,320 кПа) составляет 30,6 л, как легко рассчитать из уравнения Менделеева-Клапейрона (1.1). В жидком же состоянии при этих условиях 1 моль воды занимает объем 18,8 см3. Поэтому можно считать, что
Δ vap V = Vg – Vl ≈ Vg
Выразив молярный объем газообразного вещества из уравнения Менделеева-Клапейрона (1.1) и поставив его в уравнение Клапейрона, придем к уравнению Клапейрона-Клаузиуса:
или в интегральной форме
при условии, что теплота испарения не зависит от температуры. Данное уравнение можно представить в виде
где коэффициент A равен константе интегрирования (A = const), а Из уравнения 2.10 видно, что график зависимости ln p = f (1/ T) представляет собой прямую линию, из углового коэффициента которой можно найти теплоту испарения (рисунок 2.1):
Рисунок 2.1 – Зависимость логарифма давления насыщенного пара от обратной температуры
Пример: Определим теплоту испарения этанола, если его температура кипения при давлении 13,33 кПа составляет 34,9°С, а при давлении 101,38 кПа равна78,4°С. Решение: Температура кипения – это температура, при которой давление насыщенного пара вещества достигает внешнего давления. При этом испарение с поверхности жидкости уже невозможно, и газообразная фаза образуется внутри жидкости. Так возникают пузыри, характерные для кипения. Таким образом, при кипении давление насыщенного пара вещества равно внешнему давлению. Составим систему уравнений на основе уравнения Клапейрона-Клаузиуса для процесса испарения (2.10):
Решив систему уравнений, получим
Теплоту испарения этанола найдем как
Δ vap H = BR = 5049·8,314 = 41958,44 Дж/моль = 41,96 кДж/моль
Пример: Найдем, какое атмосферное давление на вершине горы, где вода кипит при 95°С. Теплота испарения воды по справочным данным составляет 40,66 кДж/моль. Решение: Известно, что при нормальном атмосферном давлении, равном 760 мм ртутного столба, температура кипения воды 100 °С. Из системы уравнений
находим
откуда p 2 = 633 мм.рт.ст.
Если известна зависимость давления насыщенного пара вещества от температуры, то для более точного решения нужно найти коэффициенты А и В уравнения Клайперона-Клаузиуса методом наименьших квадратов. Зная численные значения этих коэффициентов, можно найти температуру кипения при любом давлении, также давление, при котором вещество закипит при определенной температуре, и молярную теплоту испарения. Для процесса возгонки – перехода из твердого состояния в газообразное – интегральная форма уравнения Клапейрона-Клаузиуса имеет аналогичный вид:
так как молярный объем любого вещества в твердом состоянии много меньше молярного объема вещества в газообразном состоянии и выполняется соотношение
Δ sub V = Vg – Vs ≈ Vg.
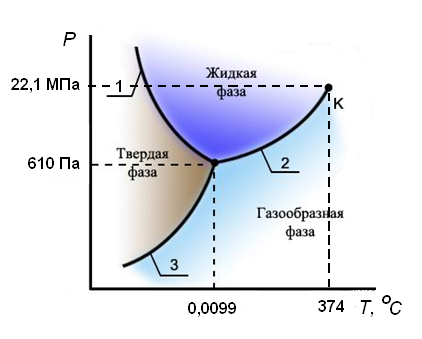
Здесь Δ sub H – теплота возгонки, а Δ sub V – изменение объема при возгонке 1 моля вещества (sub – сокращение от английского слова sublimation – сублимация, возгонка). Зависимости давления насыщенного пара от температуры для различных фазовых превращений в равновесных условиях, вытекающие из уравнения Клапейрона-Клаузиуса, могут быть представлены в виде диаграммы состояния однокомпонентной системы. На рисунке 2.2 в качестве примера приведена диаграмма состояния воды.
Рисунок 2.2 – Диаграмма состояния воды в области невысоких давлений (приведена схематично без соблюдения масштаба)
На диаграмме видны: - три области давлений и температур, при которых устойчиво существуют твердая (лед), жидкая и газообразная фазы; - три линии, разделяющие эти области и отвечающие равновесному сосуществованию твердой и жидкой фаз (линия 1), твердой и газообразной фаз (3), жидкой и газообразной фаз(2); - точка, в которой сходятся три линии, что соответствует равновесному сосуществованию трех фаз – твердой, жидкой и газообразной – так называемая, тройная точка. Рассчитаем число степеней свободы в состоянии, которому соответствует тройная точка:
т.е. система нонвариантна. Это означает, что существуют только одно определенное значение температуры (0,0099°С) и одно определенное значение давления насыщенного пара воды (610 Па), при которых сосуществуют три фазы. Изменение хотя бы одного из параметров – температуры или давления – приводит к изменению числа фаз в системе. Так как сосуществованию трех фаз соответствует строго определенная температура, тройную точку воды используют для создания эталона температуры. Первичный государственный эталон температуры хранится в Санкт-Петербурге во Всероссийском научно-исследовательском институте метрологии им. Д. И. Менделеева. В любой точке, лежащей на линиях, соответствующих равновесию между двумя фазами, число степеней свободы равно:
Это означает, что, сохраняя двухфазное равновесие, независимо можно менять только один параметр – или давление, или температуру. Второй параметр будет изменяться в соответствии с уравнением Клапейрона-Клаузиуса. 2.1.1 Многовариантное задание №3 «Анализ фазового равновесия жидкость – пар в однокомпонентной системе»
1. Для вещества А, заданного в таблице 2.1, используя данные справочника [2] по зависимости температуры кипения веществ от давления, постройте кривую испарения в координатах p = f (T)и ln p = f (1/Т). 2. Определите коэффициенты уравнения ln p = 3. Вычислите теплоту испарения Δ vap Н для вещества А (кДж /моль), используя коэффициент В, найденный в п. 2. 4. Вычислите температуру кипения при р = 1,0132·105 Па. Сопоставьте ее с табличным значением. 5. Вычислите давление насыщенного пара при температуре t x, указанной в задании (таблица 2.1). Таблица 2.1 – Варианты заданий
Двухкомпонентные системы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.210 (0.194 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
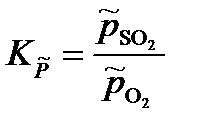
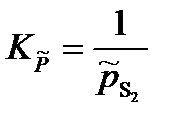
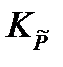 = 2,59·10-2.
= 2,59·10-2.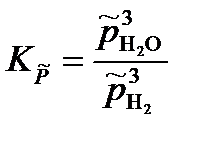
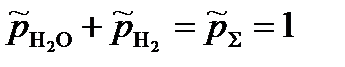
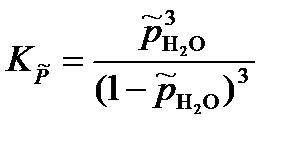
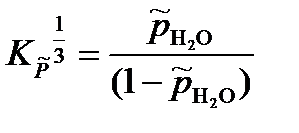
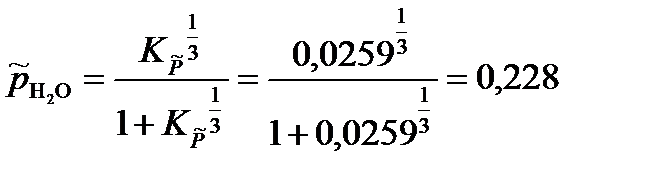
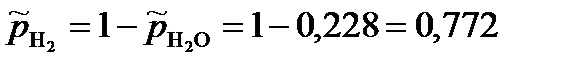
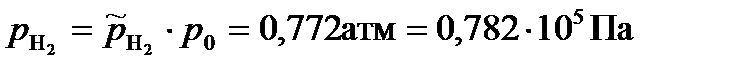
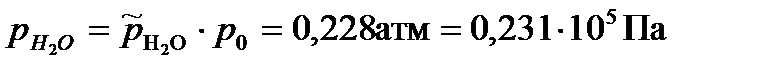
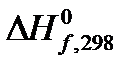 из «Краткого справочника физико-химических величин» [2] определите изобарный тепловой эффект химической реакции А (таблица 1.1) QP =
из «Краткого справочника физико-химических величин» [2] определите изобарный тепловой эффект химической реакции А (таблица 1.1) QP = 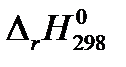 (в кДж) при условии, что все вещества, участвующие в реакции, находятся в идеальном газообразном состоянии.
(в кДж) при условии, что все вещества, участвующие в реакции, находятся в идеальном газообразном состоянии.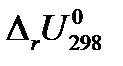 при условии, что все вещества, участвующие в реакции, находятся в идеальном газообразном состоянии.
при условии, что все вещества, участвующие в реакции, находятся в идеальном газообразном состоянии.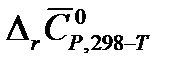 (в Дж/К). Температуру Т для своего варианта возьмите из таблицы 1.1.
(в Дж/К). Температуру Т для своего варианта возьмите из таблицы 1.1.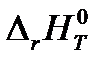 (в кДж), используя найденные ранее значения
(в кДж), используя найденные ранее значения 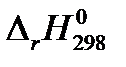 и
и 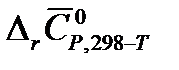 .
.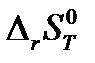 (в Дж/К) в результате реакции А при температуре Т и стандартном давлении, используя рассчитанные в п. 1.8. значения изменения энтропии при температуре 298 К и
(в Дж/К) в результате реакции А при температуре Т и стандартном давлении, используя рассчитанные в п. 1.8. значения изменения энтропии при температуре 298 К и 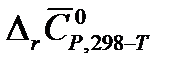 .
.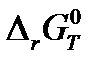 (Дж) для химической реакции А при температуре 298 К и при температуре Т.
(Дж) для химической реакции А при температуре 298 К и при температуре Т.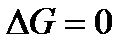
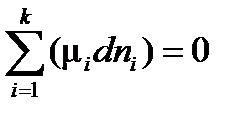 ,
,
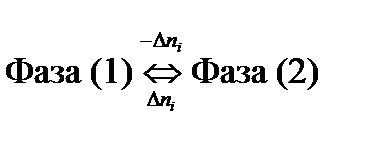 ,
,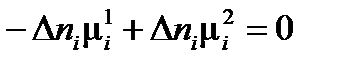 ,
,
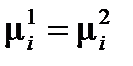 ,
,
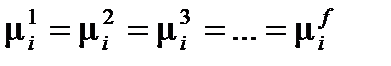 ,
,
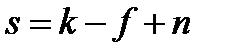 ,
,
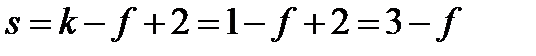 ,
,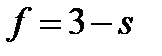
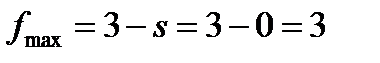
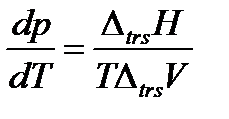
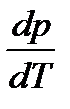 с теплотой перехода одного моля вещества из одной фазы в другую Δ trs H (trs – сокращение от английского слова transition – переход, превращение) и изменением молярного объема при фазовом переходе Δ trs V при температуре фазового превращения. Насыщенным называется пар, находящийся в равновесии с жидкостью или твердой фазой.
с теплотой перехода одного моля вещества из одной фазы в другую Δ trs H (trs – сокращение от английского слова transition – переход, превращение) и изменением молярного объема при фазовом переходе Δ trs V при температуре фазового превращения. Насыщенным называется пар, находящийся в равновесии с жидкостью или твердой фазой.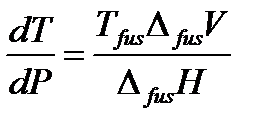
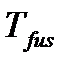 – температура плавления вещества (fus – сокращение от английского слова fusion – плавление),
– температура плавления вещества (fus – сокращение от английского слова fusion – плавление), 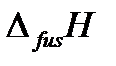 – теплота плавления одного моля вещества,
– теплота плавления одного моля вещества, 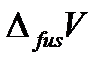 – изменение молярного объема вещества при фазовом переходе из твердого состояния в жидкое.
– изменение молярного объема вещества при фазовом переходе из твердого состояния в жидкое.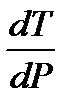 . Так как T > 0 и Δ fus H > 0, то знак производной определяется знаком Δ fus V. Для большинства веществ объем при плавлении увеличивается Δ fus V > 0 и, следовательно,
. Так как T > 0 и Δ fus H > 0, то знак производной определяется знаком Δ fus V. Для большинства веществ объем при плавлении увеличивается Δ fus V > 0 и, следовательно, 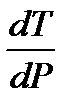 > 0. Поэтому для большинства веществ с ростом давления температура плавления увеличивается.
> 0. Поэтому для большинства веществ с ростом давления температура плавления увеличивается.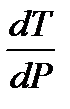 < 0. Поэтому для воды, висмута, галлия с ростом давления температура плавления уменьшается
< 0. Поэтому для воды, висмута, галлия с ростом давления температура плавления уменьшается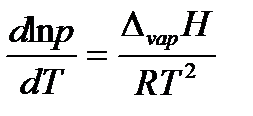
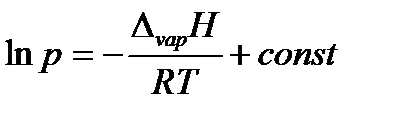
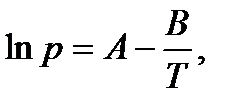
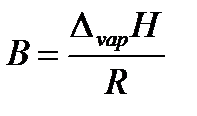 .
.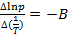 , а Δ vap H = B · R
, а Δ vap H = B · R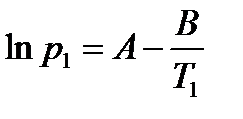
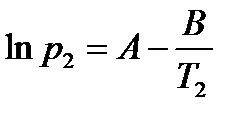
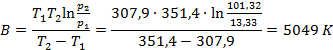
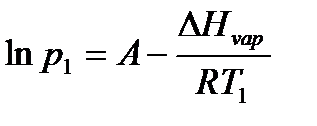
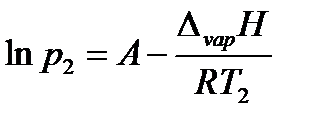
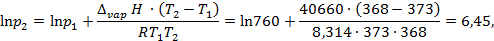
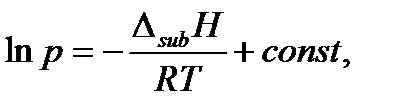
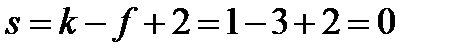 ,
,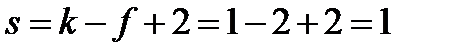
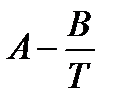 .
.


