Диаграмма плавкости, компоненты которой неограниченно растворимы друг в друге в жидком и в твердом состояниях

 

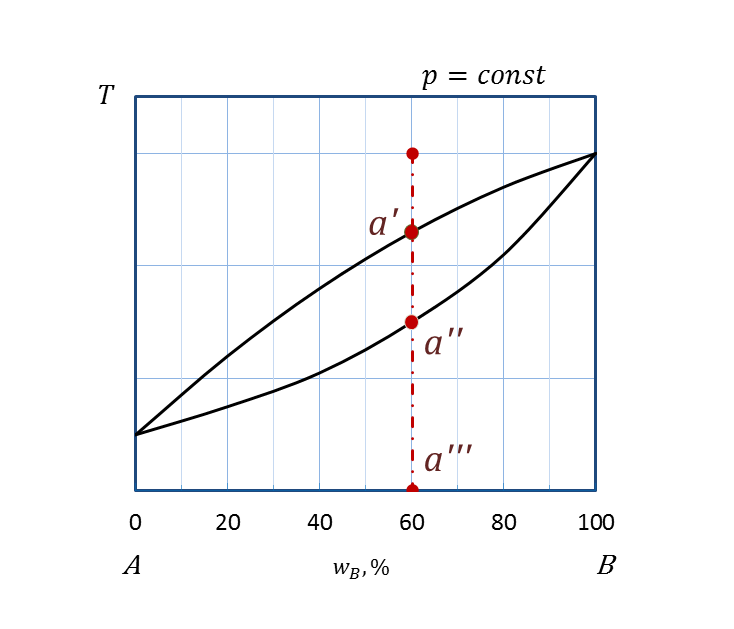
Неограниченная растворимость компонентов и в жидком и твердом агрегатных состояниях проявляется на диаграммах (рисунок 2.25) так же, как и на диаграммах состояниях жидкость – пар.

Твердые растворы  – это однородные кристаллические или аморфные фазы, сохраняющие однородность при изменении соотношения между компонентами.

Частный случай твердых растворов – изоморфные смеси или твердые растворы замещения. В таких растворах общая кристаллическая решетка построена веществами с близкими кристаллографическими характеристиками, размером частиц и химической природой. Замещение частиц происходит неупорядоченно (статистически).

Непрерывные твердые растворы замещения подобны неограниченно смешивающимся жидкостям, а диаграммы плавкости похожи на соответствующие диаграммы перегонки, подчиняются правилам Розебома, схожим с законами Гиббса-Коновалова.

I правило Розебома: твердый раствор по сравнению с сосуществующей с ним жидкостью относительно обогащен тем компонентом, добавление которого повышает температуру начала равновесной кристаллизации.

II правило Розебома: в точках экстремумов диаграмм плавкости равновесные твердые и жидкие фазы имеют одинаковый состав. В этих точках линии ликвидуса и солидуса имеют общую касательную (рисунок 2.25 б,в).

Анализ диаграммы состояния (рисунок 2.25 a) показывает, что выше кривой ликвидуса в области I система является гомогенной. В этой области находится двухкомпонентный расплав или раствор компонентов A и B. При охлаждении системы, например, состава a ’ (рисунок 2.26) по достижении кривой ликвидуса начинается кристаллизация двухкомпонентного твердого раствора. Фигуративная точка a ’ отвечает началу выпадения кристаллов, точка a ’’ на кривой солидуса – температуре конца кристаллизации. В интервале температур a ’ a ’’ (область II) система является гетерогенной, т.е. двухфазной, состоит из двухкомпонентных расплава и твердого раствора. Ниже температуры, отвечающей точке a ’’, система вновь гомогенная, в области III находится одна фаза - твердый раствор А и В.

Анализ диаграмм состояния с точками экстремумов (рисунок 2.25 б,в) проводят аналогично. Особенностью этих диаграмм является наличие двух гетерогенных областей сосуществования равновесных расплава и твердого раствора (области II, III).

В области существования гомогенного твердого раствора возможно уменьшение растворимости системы, что проявляется в появлении линии, ограничивающей область распада твердых растворов  (рисунок 2.27). Это явление называют разрывом сплошности твердого раствора. Кривая akb показывает принципиальную возможность распада гомогенного твердого раствора на два взаимно насыщенных твердых раствора компонента B в A и компонента A в B. При быстром охлаждении разрыва сплошности может не быть, тогда система останется в термодинамически неустойчивом состоянии твердого раствора.

 

Tfus .А

Tfus .В

I II III

a б                                     в

I II                     III        IV

Tfus .А

Tfus .А

Tfus .В

Tfus .В

I II                  III        IV

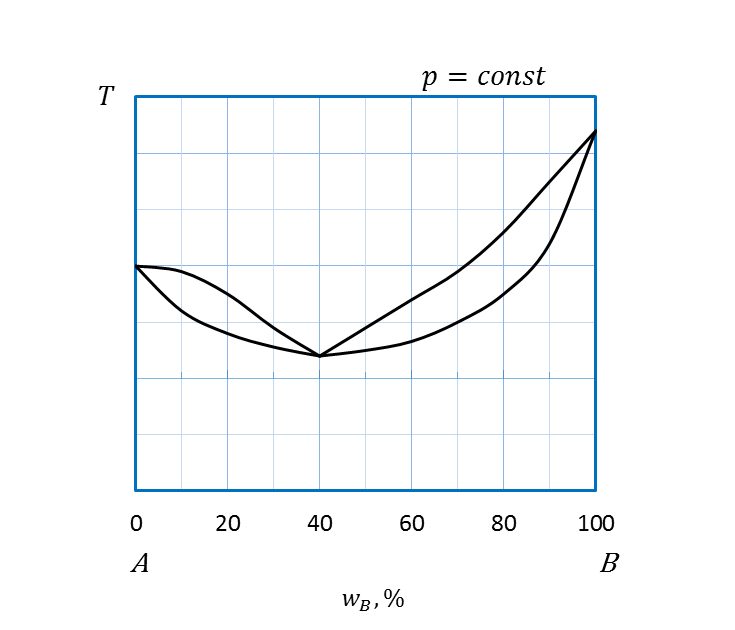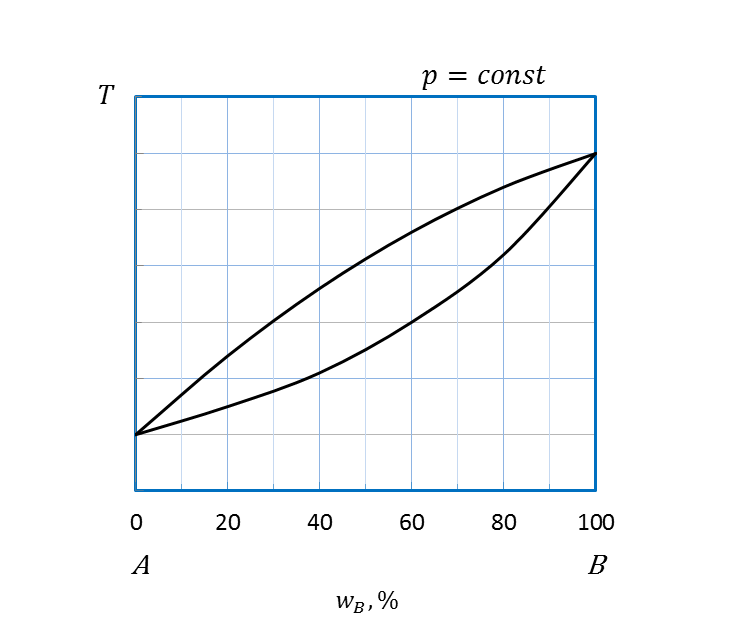
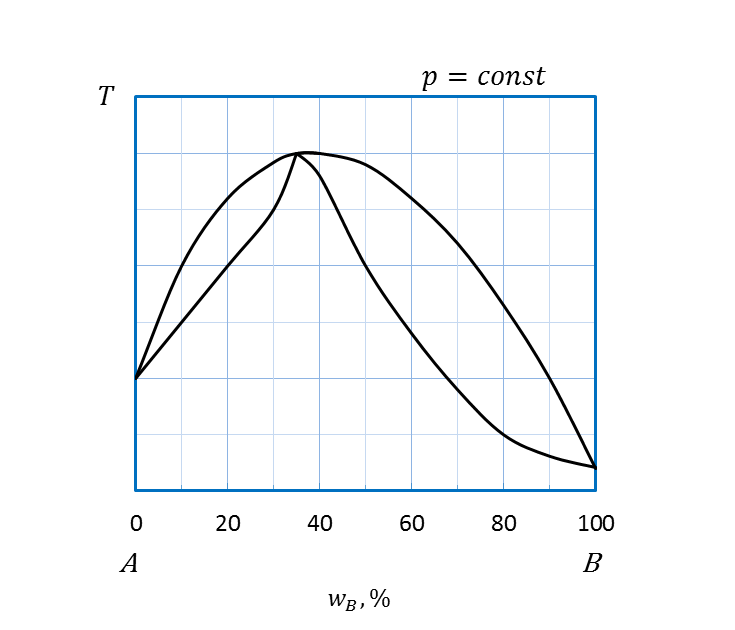
Области:

а: I – двухкомпонентный расплав A и B;

II – двухкомпонентный расплав A и B и твердый раствор компонентов А и В;

III – твердый раствор А и В;

б,в: I –двухкомпонентный расплав A и B;

II, III – двухкомпонентный расплав A и B и твердый раствор А и В;

IV – твердый раствор А и В.

 

Рисунок 2.25 - Диаграммы состояния А – B, компоненты которых полностью растворимы друг в друге в жидком и твердом состояниях

 

Рисунок 2.26 - Диаграмма состояния A – B.

Процесс охлаждения расплава a

 

Tfus .В

Tfus .А

k a                    b

 

 

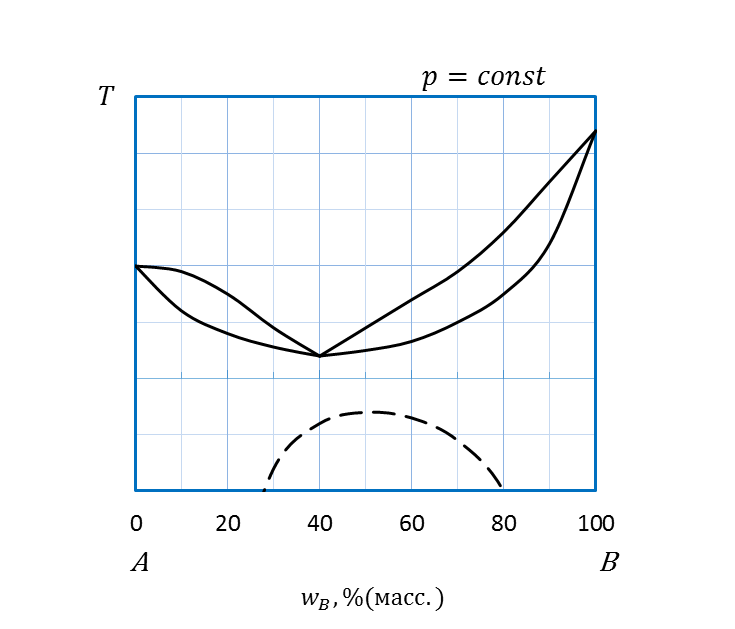
Рисунок 2.27 - Диаграмма состояния A – B.

Распад твердого раствора