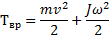Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Гироскоп. Работа при вращении тела. Кинетическая энергия вращающегося тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гироскоп Существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения).
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения тела. Так, вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновременно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей 1 и 2.
Рассмотрим одну из разновидностей гироскопов — гироскоп на кардановом подвесе. Дискообразное тело — гироскоп — закреплено на оси АА, которая может вращаться вокруг перпендикулярной ей оси ВВ, которая, в свою очередь, может поворачиваться вокруг вертикальной оси DD. Все три оси пересекаются в одной точке С, являющейся центром масс гироскопа и остающейся неподвижной, а ось гироскопа может принять любое направление в пространстве. Силами трения в подшипникax всех трех осей и моментом импульса колец пренебрегаем.
Чтобы ось гироскопа изменила свое направление в пространстве, необходимо отличие от нуля момента внешних сил. Если момент внешних сил, приложенных к вращающемуся гироскопу, относительно его центра масс отличен от нуля, то наблюдается явление, получившее название гироскопического эффекта. Оно состоит в том, что под действием пары сил F, приложенной к оси вращающегося гироскопа, ось гироскопа 0101 (рис.) поворачивается вокруг прямой 0303, а не вокруг прямой 02 (O 3 О3 и F перпендикулярны плоскости чертежа). Гироскопический эффект объясняется следующим образом. Момент Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т.д.) положение оси гироскопа в пространстве сохраняется. Следовательно, ось гироскопа вместе с рамами карданова подвеса поворачивается относительно движущегося устройства. Поворот рам карданова подвеса с помощью определенных приспособлений включает рули управления, которые возвращают движение к заданному курсу.
2. Кинетическая энергия вращающегося тела. Работа при вращательном движении
Если момент
Разделим и умножим правую часть на dt:
Учитывая
Интегрируя выражение (2), получаем формулу для работы по изменению угловой скорости тела от начального значения
Выражение (3) можно интерпретировать и так: работа, совершаемая при вращении тела на угол Мощность NBp можно записать в виде:
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 637; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

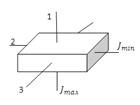 Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис.).
Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис.).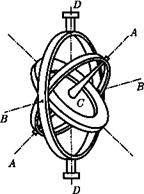 Свойство свободных осей сохранять положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью ω около своей оси симметрии, являющей свободной осью.
Свойство свободных осей сохранять положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью ω около своей оси симметрии, являющей свободной осью.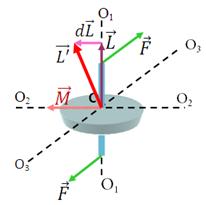 Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (например, с помощью намотанной на ось веревочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения.
Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (например, с помощью намотанной на ось веревочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения.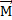 пары сил
пары сил 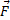 направлен вдоль прямой 0202. За время dt момент импульса
направлен вдоль прямой 0202. За время dt момент импульса 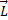 гироскопа получит приращение
гироскопа получит приращение 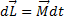 (направление
(направление 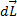 совпадает с направлением
совпадает с направлением 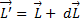 . Направление вектора
. Направление вектора 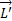 совпадает с новым направлением оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется вокруг прямой О303. Если время действия силы мало, то, хотя момент сил
совпадает с новым направлением оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется вокруг прямой О303. Если время действия силы мало, то, хотя момент сил 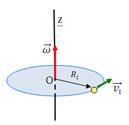 Если тело вращается вокруг неподвижной оси, то говорят, что оно обладает кинетической энергией вращения Твр. Получим выражение для этой величины. Предположим, что вращающееся тело, состоит из небольших частиц, каждая из которых имеет массу m i. Если ri - расстояние по перпендикуляру от оси вращения Oz до любой такой частицы (радиус вращения i-й частицы), то линейная скорость частицы
Если тело вращается вокруг неподвижной оси, то говорят, что оно обладает кинетической энергией вращения Твр. Получим выражение для этой величины. Предположим, что вращающееся тело, состоит из небольших частиц, каждая из которых имеет массу m i. Если ri - расстояние по перпендикуляру от оси вращения Oz до любой такой частицы (радиус вращения i-й частицы), то линейная скорость частицы  Полная кинетическая энергия всего тела равна сумме кинетических энергий всех составляющих его частиц:
Полная кинетическая энергия всего тела равна сумме кинетических энергий всех составляющих его частиц: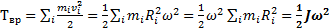 (1)
(1) 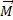 внешних сил относительно неподвижной оси вращения твердого тела отличен от нуля, то угловая скорость ω и кинетическая энергия Твр тела изменяются, т. е. совершается работа. Дифференциал этой работы равен:
внешних сил относительно неподвижной оси вращения твердого тела отличен от нуля, то угловая скорость ω и кинетическая энергия Твр тела изменяются, т. е. совершается работа. Дифференциал этой работы равен:

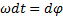 , получим
, получим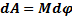 (2)
(2)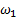 до конечного значения
до конечного значения 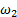
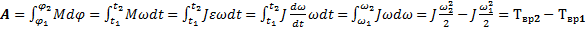 (3)
(3)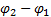 вокруг неподвижной оси, равна изменению кинетической энергии его вращательного движения.
вокруг неподвижной оси, равна изменению кинетической энергии его вращательного движения.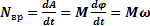 (3)
(3) В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости
В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 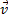 центра масс, и вращения с угловой скоростью
центра масс, и вращения с угловой скоростью 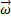 вокруг мгновенной оси, проходящей через центр масс. Но если тело вращается и при этом его центр масс перемещается поступательно (вспомните движение прыгуна в воду в одном из предыдущих примеров), то оно имеет кинетическую энергию как поступательного, так и вращательного движений. Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс и кинетической энергии его вращения относительно центра масс:
вокруг мгновенной оси, проходящей через центр масс. Но если тело вращается и при этом его центр масс перемещается поступательно (вспомните движение прыгуна в воду в одном из предыдущих примеров), то оно имеет кинетическую энергию как поступательного, так и вращательного движений. Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс и кинетической энергии его вращения относительно центра масс: