
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Механическое движение. Скорость.Содержание книги
Поиск на нашем сайте
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ Глава № 1. Кинематика
ЛЕКЦИЯ 1, 2 Третий закон Ньютона справедлив не всегда. Вполне строго он выполняется при непосредственном соприкосновении тел, а также при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел. 2.4 Закон сохранения импульса Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими к данной системе. В соответствии с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними называют силы, с которыми на данное тело воздействуют остальные тела системы, внешними - силы, обусловленные воздействием тел, не принадлежащих системе. В случае, когда внешние силы отсутствуют, система называется замкнутой. Рассмотрим систему, состоящую из n точечных частиц. В частности, 1 в виде так:0й системы можно представить и твердое тело Присвоим частицам номера от 1 до n и обозначим силу, действующую со стороны i-й частицы на j-ю через Fij. Кроме того, на частицы могут действовать внешние силы. Обозначим результирующую силу, действующую со стороны внешних тел на i-ю частицу, через Фi. Напишем уравнение движения для каждой из частиц системы:
………………………………..
Сложим почленно все n выписанных уравнений (2.13). Заметим, что в сумму справа войдет, например, такая пара: F21 из первого уравнения и F12 - из второго, Но согласно третьему закону Ньютона:
Поэтому все внутренние силы уничтожаются при суммировании. С другой стороны, после такого суммирования слева будет стоять производная от суммы импульсов всех частиц, т. е. от полного импульса системы
В итоге получаем
Напомним, что Ф i - это результирующая внешняя сила, действующая на i-ю частицу системы. Или В незамкнутой системе изменение импульса системы равно импульсу внешней силы. Импульс системы материальных тел не может быть изменен внутренними силами, а может быть изменен только внешними силами.
Предположим, что векторная сумма внешних сил равна нулю 2.5 Цент масс
Импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Найдем ее координаты. Запишем уравнение для изменения импульса материальных точек:
Здесь мы вначале учли определение импульса одной час тицы, затем домножили и разделили выражение на полную массу всей системы Преобразуем выражение (2.15) дальше:
Выражение (2.16) - уравнение движения центра масс. Масса сосредоточена в точке с радиусом-вектором
Эта точка и называется центром масс или центром инерции системы частиц. В проекции на ось Х, например,
Итак: если всю массу системы частиц (или в частном случае твердого тела) сосредоточить в ее центре масс, то импульс этой воображаемой частицы будет равен полному импульсу системы. Работа. Мощность
Изменение механического движения тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы. Рассмотрим движение материальной точки в некотором силовом поле
где α - угол между векторами F и dS (рис.). Работа, совершаемая силой
Вспоминая геометрический смысл интеграла, получаем, что работа А численно равна площади криволинейной фигуры на графике зависимости Fs от S (рис.). В частном случае перемещения частицы по прямолинейному участку пути под действием постоянной силы А = FScosα. (2.25)
Если угол α тупой (cosα< 0), работа отрицательна. В этом случае Fs и dS противоположны по направлению, поэтому силу При α = π/2 работа равна нулю. В этом случае сила лишь искривляет траекторию движущегося тела. Таково, например, действие центростремительной силы на материальную точку, равномерно движущуюся по окружности. Если на тело одновременно действуют несколько сил В качестве единицы работы в СИ принято, согласно определению (2.25), произведение единицы силы на единицу перемещения, т. е. Н • м. Эта величина называется джоулем (Дж): Дж = Н∙м. Практически часто важно знать не только работу, совершенную силами, но и то время, за которое работа произведена. Из двух механизмов, совершающих одну и ту же работу, обычно ценнее тот, который совершает эту работу за меньший промежуток времени. Поэтому наряду с работой вводится в рассмотрение величина, называемая мощностью. Мощность N - это работа, производимая в единицу времени. Если сила
Размерность мощности в СИ - ватт:
Закон сохранения энергии
Сумма кинетической и потенциальной энергий называется полной энергией. Пусть дана изолированная замкнутая система, состоящая из точек массами m 1, m 2, … mn, движущихся со скоростями v 1, v 2, … vn и взаимодействующих между собой.Тогда уравнение движения для каждой точки:
……………………………….
Домножим каждое уравнение на
……………………………….
Так как
………………..
Величину
……………………..
Или
То, что полная энергия остается неизменной демонстрируется на примере свободного падения тела без учета сопротивления среды. Этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга.
Гироскоп Существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения).
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения тела. Так, вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновременно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей 1 и 2.
Рассмотрим одну из разновидностей гироскопов — гироскоп на кардановом подвесе. Дискообразное тело — гироскоп — закреплено на оси АА, которая может вращаться вокруг перпендикулярной ей оси ВВ, которая, в свою очередь, может поворачиваться вокруг вертикальной оси DD. Все три оси пересекаются в одной точке С, являющейся центром масс гироскопа и остающейся неподвижной, а ось гироскопа может принять любое направление в пространстве. Силами трения в подшипникax всех трех осей и моментом импульса колец пренебрегаем.
Чтобы ось гироскопа изменила свое направление в пространстве, необходимо отличие от нуля момента внешних сил. Если момент внешних сил, приложенных к вращающемуся гироскопу, относительно его центра масс отличен от нуля, то наблюдается явление, получившее название гироскопического эффекта. Оно состоит в том, что под действием пары сил F, приложенной к оси вращающегося гироскопа, ось гироскопа 0101 (рис.) поворачивается вокруг прямой 0303, а не вокруг прямой 02 (O 3 О3 и F перпендикулярны плоскости чертежа).
Гироскопический эффект объясняется следующим образом. Момент Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т.д.) положение оси гироскопа в пространстве сохраняется. Следовательно, ось гироскопа вместе с рамами карданова подвеса поворачивается относительно движущегося устройства. Поворот рам карданова подвеса с помощью определенных приспособлений включает рули управления, которые возвращают движение к заданному курсу.
2. Кинетическая энергия вращающегося тела. Работа при вращательном движении
Если момент
Разделим и умножим правую часть на dt:
Учитывая
Интегрируя выражение (2), получаем формулу для работы по изменению угловой скорости тела от начального значения
Выражение (3) можно интерпретировать и так: работа, совершаемая при вращении тела на угол
Мощность NBp можно записать в виде:
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ Глава № 1. Кинематика
ЛЕКЦИЯ 1, 2 Тема: Механическое движение. Скорость. 1.1 Введение Физика – это наука о природе. Она возникла из стремления понять и описать окружающий нас мир. Мир наш необычайно сложен и интересен: Солнце, Луна, приливы, отливы, землетрясения, день, ночь, море, облака, горы, ветер, животный и растительный мир. Человек – часть этого мира пытается понять как устроен он. Возможно ли это? Из нашего общего опыта мы знаем, что мир познаваем и что многое известно о физических законах, которые приводят к тому многообразию явлений, которые окружают нас. Физические законы образуются в результате обобщения экспериментальных данных и выражают объективные закономерности, существующие в природе. Физика – это раздел естествознания, который изучает наиболее общие свойства и формы материи. Материя – это философская категория, изображающая объективную реальность, существующую вне сознания человека, которая отображается, копируется, фотографируется чувствами человека и существует независимо от них. Известно два вида материи: вещество и поле. К веществу относятся, например, атомы, молекулы, и все построенные из них тела. Второй вид материи образуют электромагнитные, гравитационные поля. Эти виды материи неразрывно связаны друг с другом и могут превращаться друг в друга. Например, электрон и позитрон (представляют собой вещество) могут превращаться в фотоны (т.е. электромагнитное поле). Механика – раздел физики, изучающий наиболее простое движение материи. Движение материи происходит в пространстве и времени, т.о. пространство и время – формы существования материи.
1.2 Механическое движение. Система отсчета. Кинематические уравнения движения Что такое движение и как его описать? На этот вопрос отвечает кинематика, описывающая движение тел. Механическое движение – это изменение положения тел или их частей в пространстве с течением времени относительно друг друга. Тело, по отношению к которому рассматривается движение какого-то другого тела, называется тело отсчета.
При поступательном движении прямая, соединяющая две произвольные точки тела, переносится параллельно себе самой. Для изучения поступательного движения тела достаточно изучить движение какой-либо одной из его точек, т. к. все точки тела движутся совершенно одинаково.
Колебаниями называются движения, повторяющиеся во времени, в окрестности некоторого положения равновесия. Например, если мы подтолкнем шарик, висящий на нити, то он будет совершать колебания около своего первоначального отвесного положения. Изучение поведения тел в механике основано на двух основных моделях тел: материальной точке и абсолютно твердом теле. Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой. Тело, конечных размеров называется абсолютно твердым, если в условиях данной задачи можно пренебречь его деформацией. Для описания положения материальной точки вводится система координат. Совокупность тела отсчета, системы координат и часов, отсчитывающих время, называется системой отсчета. Число независимых движений, которые может совершать тело, называют числом степеней свободы. Число степени свободы – это число, которое можно задать для описания положения тел системы. Например, материальная точка имеет три степени свободы если она двигается в пространстве: поступательное движение вдоль оси x, y, z; при движении на плоскости достаточно две координатные оси, следовательно в этом случае число степеней свободы равно двум, а при движении вдоль прямой – число степеней свободы равно одному.Абсолютно твердое тело может обладать тремя степенями свободы поступательного движения, тремя степенями свободы вращательного движения, если тело не абсолютно твердое и его части могут смещаться друг относительно друга, то необходимо вводить еще дополнительные три степени свободы колебательного движения. Выбор системы отсчета позволяет описать движение рассматриваемых тел. Координаты – это функции времени: x (t) = x; y (t) = y; z (t) = z (1.1)
Если указать не только начальное положение точки, но и указать направление движения, то задача упрощается (вместо трех уравнений – получится одно уравнение):
где Уравнения (1) и (2) равносильны. Если ввести единичные векторы характеризующие направление осей координат, то положение точки можно выразить через данные вектора. Свойства векторов:
Сумма трех векторов:
Линия, описывающая движение тела, называется траекторией. Длина траектории от точки М1до точки М2 – это путь. Путь Модуль малого приращения равен длине соответствующей ему дуги траектории:
В зависимости от формы траектории различают прямолинейное и криволинейное движения точки.
1.3 Скорость Для характеристики движения материальной точки вводят векторную физическую величину – скорость. Пусть материальная точка движется по криволинейной траектории так, что в момент t1 она находилась в точке М1, а в момент времени При движении материальной точки относительно системы отсчета меняется направление перемещения:
Время, потраченное на перемещение
Вектором средней скорости называют отношение приращения
Если известно
Вектор средней скорости характеризует только быстроту движения материальной точки за минимальный промежуток времени. Направление вектора совпадает с направлением перемещения
По мере уменьшения
Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным движением. В этом случае пользуются скалярной величиной, называемой средней путевой скоростью. Она равна отношению пройденного пути к интервалу времени, в течение которого был совершен этот путь:
Если численное значение мгновенной скорости остается во время движения точки неизменным, то такое движение называют равномерным. Длина пути, пройденного точкой за время
1.4 Ускорение. При движении материальной точки её скорость может непрерывно меняться как по величине (модулю), так и по направлению. Пусть за время
Ускорением или мгновенным ускорением, точки в момент времени t называют векторную величину
Ускорение измеряется в м/с2.
Ускорение, характеризующее изменение скорости по модулю, называется тангенциальным ускорением:
Таким образом, тангенциальная составляющая ускорения описывает изменение модуля скорости и направлена вдоль скорости, т. е. по касательной к траектории.
Ускорение, характеризующее изменение скорости по модулю, называется тангенциальным ускорением. Нормальная составляющая ускорения возникает только при криволинейном движении.
Величину R называют радиусом кривизны траектории.. В частном случае вектор нормального ускорения направлен к центру и называется центростремительным.
Тангенциальное и нормальное ускорения взаимно перпендикулярны между собой, поэтому модуль полного ускорения:
1. Равномерное прямолинейное движение.. Это движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения.
2. Неравномерное прямолинейное движение. Это движение, при котором направление скорости остается постоянным, а модуль изменяется.
3. Равномерное криволинейное движение. Это движение, при котором модуль скорости остается постоянным, а вектор скорости меняет свое направление.
1.6 Равномерное движение материальной точки по окружности При описании вращательного движения тела величинами S, v и а (путь, скорость, ускорение) пользоваться неудобно, т. к. различные точки (с разными радиусами вращения R) тела за один и тот же промежуток времени совершают разные перемещения и движутся с различными скоростями и ускорениями. Поэтому здесь вводятся специальные, так называемые угловые величины: угол поворота φ, угловая скоростьω, угловое ускорение ε. Для различных точек вращающегося тела они одинаковы.
Угловая скорость определяет изменение угла φ (т. е. Δφ) в единицу времени. Измеряя углы в радианах, а время в секундах, в качестве единицы угловой скорости выбирают угловую скорость такого движения, при котором угол φ меняется на один радиан за одну секунду, эту единицу угловой скорости можно обозначить рад/с; обычно ее обозначают просто 1/с или с -1. При равномерном вращении (ω= const) зависимость угла от времени определяется формулой:
Пусть Т - период обращения частицы, т. е. время совершения ею одного оборота вокруг центра вращения О. За время Δt = Т угол φ возрастает на 2π, т. е. Δφ = 2π. Поэтому
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.101.177 (0.013 с.) |

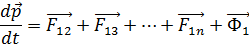
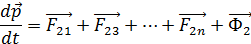
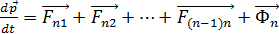 (2.13)
(2.13)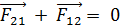 .
. 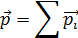
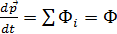 (2.14)
(2.14)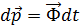
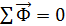 , т.е. система частиц замкнута. В этом случае
, т.е. система частиц замкнута. В этом случае 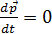 и, следовательно,
и, следовательно, 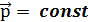 , т. е. в замкнутой системе полный импульс системы частиц сохраняется. Это утверждение называют законом сохранения импульса.
, т. е. в замкнутой системе полный импульс системы частиц сохраняется. Это утверждение называют законом сохранения импульса.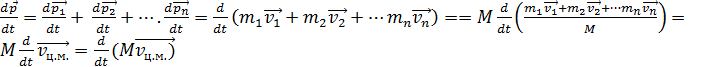 (2.15)
(2.15)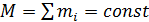 (при этом величина дроби не изменилась), ввели некоторый вектор
(при этом величина дроби не изменилась), ввели некоторый вектор 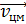 Полученное выражение показывает, что полный импульс системы частиц может быть представлен как
Полученное выражение показывает, что полный импульс системы частиц может быть представлен как 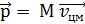 .
. 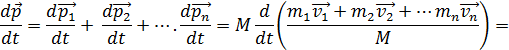
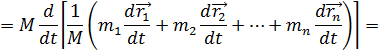
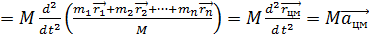 (2.16)
(2.16)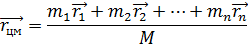
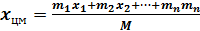 (2.17)
(2.17)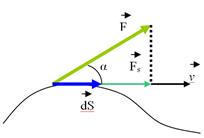 Если на частицу в каждой точке пространства действует определенная сила, то всю эту совокупность сил в пространстве называют силовым полем. Силовое поле называется однородным и постоянным, когда силы поля имеют повсюду одинаковую величину и неизменное направление и не зависят от времени.
Если на частицу в каждой точке пространства действует определенная сила, то всю эту совокупность сил в пространстве называют силовым полем. Силовое поле называется однородным и постоянным, когда силы поля имеют повсюду одинаковую величину и неизменное направление и не зависят от времени.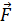 . Если под действием силы
. Если под действием силы 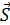 , тогда элементарная работа:
, тогда элементарная работа: 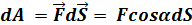 (2.23)
(2.23)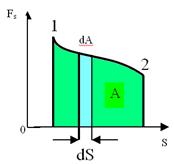
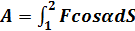 (2.24)
(2.24)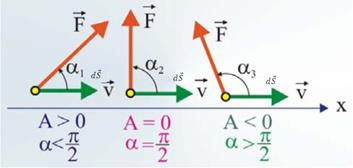 Если сила и перемещение образуют острый угол (cosα> 0), то работа положительна. В этом случае составляющая Fs силы совпадает по направлению с вектором dS. Поэтому силу
Если сила и перемещение образуют острый угол (cosα> 0), то работа положительна. В этом случае составляющая Fs силы совпадает по направлению с вектором dS. Поэтому силу 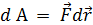 , а
, а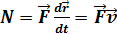 (2.26)
(2.26)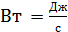
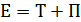
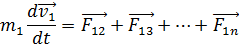
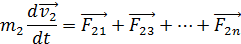
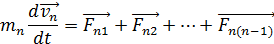
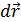 , учитывая
, учитывая 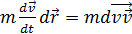
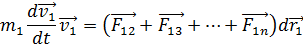
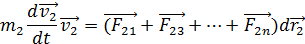
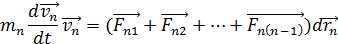
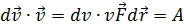 получаем
получаем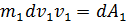
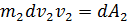
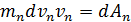
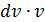 можно представить как
можно представить как 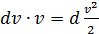 , а
, а 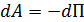 тогда
тогда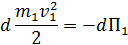
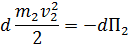
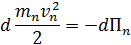
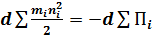
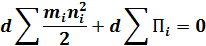
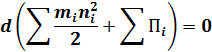
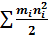 – сумма - полная кинетическая энергия всех точек
– сумма - полная кинетическая энергия всех точек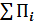 – полная потенциальная энергия всех точек
– полная потенциальная энергия всех точек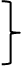
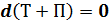
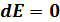 (2.36)
(2.36) 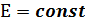
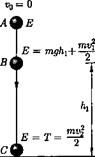 Закон сохранения энергии: Для замкнутой изолированной системы, в которой действуют только консервативные силы, полная механическая энергия остается постоянной. Она переходит из одного вида в другой.
Закон сохранения энергии: Для замкнутой изолированной системы, в которой действуют только консервативные силы, полная механическая энергия остается постоянной. Она переходит из одного вида в другой.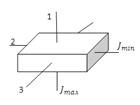 Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис.).
Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис.).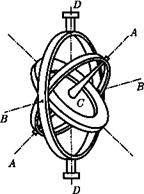 Свойство свободных осей сохранять положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью ω около своей оси симметрии, являющей свободной осью.
Свойство свободных осей сохранять положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью ω около своей оси симметрии, являющей свободной осью.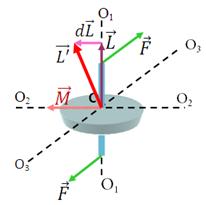 Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (например, с помощью намотанной на ось веревочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения.
Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (например, с помощью намотанной на ось веревочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения.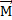 пары сил
пары сил 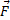 направлен вдоль прямой 0202. За время dt момент импульса
направлен вдоль прямой 0202. За время dt момент импульса 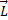 гироскопа получит приращение
гироскопа получит приращение 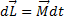 (направление
(направление 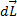 совпадает с направлением
совпадает с направлением 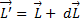 . Направление вектора
. Направление вектора 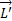 совпадает с новым направлением оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется вокруг прямой О303. Если время действия силы мало, то, хотя момент сил
совпадает с новым направлением оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется вокруг прямой О303. Если время действия силы мало, то, хотя момент сил 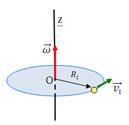 Если тело вращается вокруг неподвижной оси, то говорят, что оно обладает кинетической энергией вращения Твр. Получим выражение для этой величины. Предположим, что вращающееся тело, состоит из небольших частиц, каждая из которых имеет массу m i. Если ri - расстояние по перпендикуляру от оси вращения Oz до любой такой частицы (радиус вращения i-й частицы), то линейная скорость частицы
Если тело вращается вокруг неподвижной оси, то говорят, что оно обладает кинетической энергией вращения Твр. Получим выражение для этой величины. Предположим, что вращающееся тело, состоит из небольших частиц, каждая из которых имеет массу m i. Если ri - расстояние по перпендикуляру от оси вращения Oz до любой такой частицы (радиус вращения i-й частицы), то линейная скорость частицы  Полная кинетическая энергия всего тела равна сумме кинетических энергий всех составляющих его частиц:
Полная кинетическая энергия всего тела равна сумме кинетических энергий всех составляющих его частиц: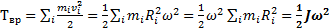 (1)
(1) 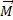 внешних сил относительно неподвижной оси вращения твердого тела отличен от нуля, то угловая скорость ω и кинетическая энергия Твр тела изменяются, т. е. совершается работа. Дифференциал этой работы равен:
внешних сил относительно неподвижной оси вращения твердого тела отличен от нуля, то угловая скорость ω и кинетическая энергия Твр тела изменяются, т. е. совершается работа. Дифференциал этой работы равен:

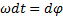 , получим
, получим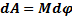 (2)
(2)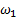 до конечного значения
до конечного значения 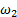
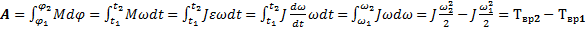 (3)
(3)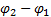 вокруг неподвижной оси, равна изменению кинетической энергии его вращательного движения.
вокруг неподвижной оси, равна изменению кинетической энергии его вращательного движения.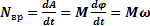 (3)
(3)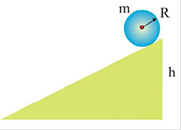 В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости
В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 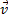 центра масс, и вращения с угловой скоростью
центра масс, и вращения с угловой скоростью 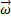 вокруг мгновенной оси, проходящей через центр масс. Но если тело вращается и при этом его центр масс перемещается поступательно (вспомните движение прыгуна в воду в одном из предыдущих примеров), то оно имеет кинетическую энергию как поступательного, так и вращательного движений. Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс и кинетической энергии его вращения относительно центра масс:
вокруг мгновенной оси, проходящей через центр масс. Но если тело вращается и при этом его центр масс перемещается поступательно (вспомните движение прыгуна в воду в одном из предыдущих примеров), то оно имеет кинетическую энергию как поступательного, так и вращательного движений. Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс и кинетической энергии его вращения относительно центра масс: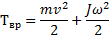
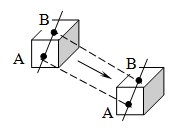 Движение тел принято разделять на несколько простых видов: поступательное, вращательное и колебательное.
Движение тел принято разделять на несколько простых видов: поступательное, вращательное и колебательное.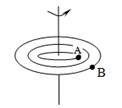 При вращательном движении тела все его точки описывают окружности в параллельных плоскостях, причем центры этих окружностей лежат на одной прямой, называемой осью вращения.
При вращательном движении тела все его точки описывают окружности в параллельных плоскостях, причем центры этих окружностей лежат на одной прямой, называемой осью вращения.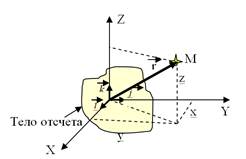
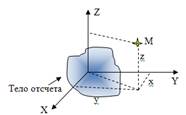 Уравнения (1), с помощью которых можно предсказывать положение точки, называется кинематическим уравнениемдвижения тела.
Уравнения (1), с помощью которых можно предсказывать положение точки, называется кинематическим уравнениемдвижения тела.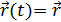 (1.2),
(1.2),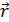 - радиус вектор, проведенный из начала координат в точку М.
- радиус вектор, проведенный из начала координат в точку М.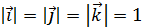
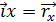 ,
, 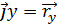 ,
, 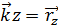
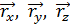 равна радиус-вектору
равна радиус-вектору 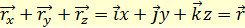 (1.3)
(1.3)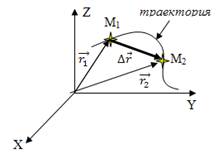
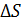 – это скалярная физическая величина равная сумме длин отрезков траектории. Вектор, соединяющий начальное положение тела с конечным, называется перемещением
– это скалярная физическая величина равная сумме длин отрезков траектории. Вектор, соединяющий начальное положение тела с конечным, называется перемещением 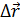 .
.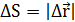 или
или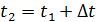 в точке М2
в точке М2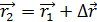
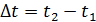
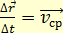 (1.4)
(1.4)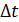 и, то можно найти перемещение точки:
и, то можно найти перемещение точки: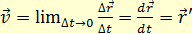 (1.5)
(1.5)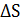 все больше будет приближаться к модулю радиус-вектору
все больше будет приближаться к модулю радиус-вектору 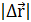 , поэтому модуль мгновенной скорости
, поэтому модуль мгновенной скорости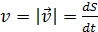 (1.6)
(1.6)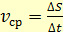 (1.7)
(1.7)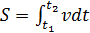 (1.8)
(1.8)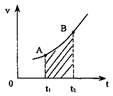
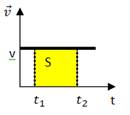
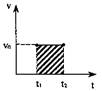 Путь равен площади криволинейной фигуры в случае неравномерного движения и площади прямоугольника, при равномерном движении.
Путь равен площади криволинейной фигуры в случае неравномерного движения и площади прямоугольника, при равномерном движении.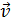 изменился на
изменился на 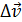 , тогда отношение вектора
, тогда отношение вектора 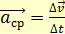 (1.9)
(1.9)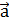 , равную пределу, к которому стремиться среднее ускорение этой точки в промежуток времени от t до
, равную пределу, к которому стремиться среднее ускорение этой точки в промежуток времени от t до 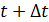 при неограниченном уменьшении
при неограниченном уменьшении 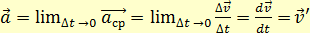 (1.10)
(1.10) 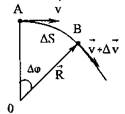
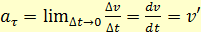 (1.11)
(1.11)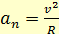 (1.12)
(1.12)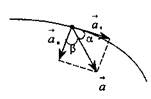 Полное ускорение равно сумме тангенциального и нормального ускорений:
Полное ускорение равно сумме тангенциального и нормального ускорений: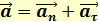 (1.13)
(1.13)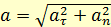 (1.14)
(1.14)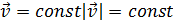 (скорость по направлению и модулю остается постоянной)
(скорость по направлению и модулю остается постоянной)
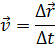 При равномерном прямолинейном движении полное перемещение равно пройденному пути
При равномерном прямолинейном движении полное перемещение равно пройденному пути
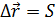
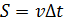 Кинематическое уравнение движения:
Кинематическое уравнение движения: 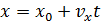
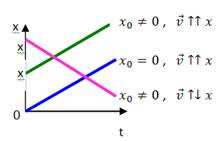
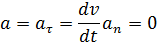 Скорость
Скорость 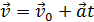 При равномерном прямолинейном движении полное перемещение равно пройденному пути
При равномерном прямолинейном движении полное перемещение равно пройденному пути
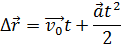 Кинематическое уравнение движения:
Кинематическое уравнение движения: 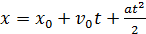
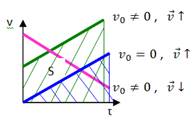
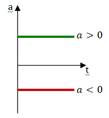
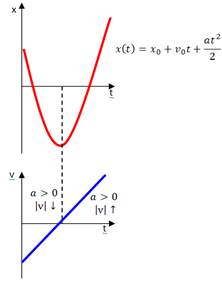
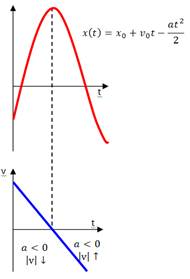
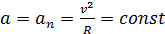 ,
, 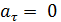
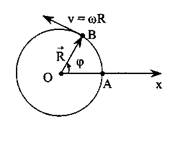 Рассмотрим движение материальной точки по окружности радиуса R (рис.). Положение частицы на окружности можно характеризовать углом φ, отсчитывая его от фиксированного радиуса, например, совпадающего по направлению с осью х (ОА на рисунке). Тогда аналогом перемещения AS вдоль окружности будет соответствующее этому перемещению изменение угла Δφ. По аналогии со скоростью прямолинейного движения введем угловую скорость точки:
Рассмотрим движение материальной точки по окружности радиуса R (рис.). Положение частицы на окружности можно характеризовать углом φ, отсчитывая его от фиксированного радиуса, например, совпадающего по направлению с осью х (ОА на рисунке). Тогда аналогом перемещения AS вдоль окружности будет соответствующее этому перемещению изменение угла Δφ. По аналогии со скоростью прямолинейного движения введем угловую скорость точки: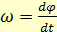 (1.15)
(1.15)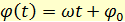 (1.16)
(1.16)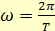 (1.17)
(1.17) 


