
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение необходимого объема выборкиСодержание книги
Поиск на нашем сайте
Пусть требуется найти минимальное число п повторений опытов, при котором среднее арифметическое Величину t определяют по справочникам при уровне значимости q и числе степеней свободы
Формулу (2.16) можно преобразовать следующим образом. Поделим числитель и знаменатель на
Учитывая, что отношение В дальнейшем изложении широко используются процедуры проверки статистических гипотез. Статистическая гипотеза – это некоторое предположение относительно свойств генеральной совокупности, проверяемое по выборке (например, гипотеза об однородности средних или дисперсий, законе распределения и т. д.). Проверка статистической гипотезы – процедура, по результатам которой гипотеза принимается Проверка статистических гипотез связана с такими распростра-ненными задачами, как сравнительная оценка различных технологических процессов по их производительности, точности, экономичности
Для проверки статистической гипотезы вычисляют значение критерия по имеющимся опытным данным. Если оно находится внутри некоторой заданной области, называемой областью принятия гипотезы (областью допустимых значений), то нулевая гипотеза принимается, в противном случае значение критерия попадает в критическуюобласть и гипотеза отвергается. Однако попадание критерия в область допустимых значений еще Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность этой ошибки задается заранее выбором уровня значимости q. (Как указывалось, типичные значения q: 0,01; 0,05; 0,1, или 1, 5 и 10 %.) Ошибка второго рода состоит в том, что гипотеза принимается,
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.206 (0.01 с.) |

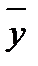 , найденное по этой выборке, отличалось бы от математического ожидания не более, чем на задан-
, найденное по этой выборке, отличалось бы от математического ожидания не более, чем на задан- . Это, по существу, задача, обратная предыдущей.
. Это, по существу, задача, обратная предыдущей. 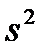 . Здесь можно использовать, например, результаты проведенных ранее исследований. Значение n определяется по формуле
. Здесь можно использовать, например, результаты проведенных ранее исследований. Значение n определяется по формуле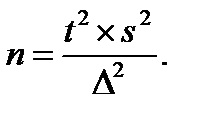 (2.16)
(2.16) , связанном с оценкой дисперсии
, связанном с оценкой дисперсии 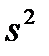 . Если эта дисперсия найдена по выборке объема, большего 120, то вместо величины t в формуле (2.16) можно пользоваться величиной
. Если эта дисперсия найдена по выборке объема, большего 120, то вместо величины t в формуле (2.16) можно пользоваться величиной  , зависящей только от уровня значимости q. Значения
, зависящей только от уровня значимости q. Значения 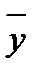 . Относительная допускаемая ошибка, %:
. Относительная допускаемая ошибка, %: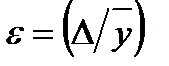
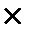 100.
100.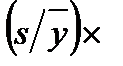 100, выраженное в процентах, – это, по определению, коэффициент вариации v, получим:
100, выраженное в процентах, – это, по определению, коэффициент вариации v, получим: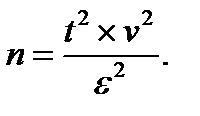 (2.17)
(2.17)


