
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка адекватности математической моделиСодержание книги
Поиск на нашем сайте
После постановки опытов, вычисления коэффициентов регрессии Рассмотрим линейное уравнение регрессии для трех факторов:
Поскольку в полученном уравнении Затем вычисляем сумму квадратов
Этот случай имеет место при недублированных опытах. Чем
где р – число коэффициентов регрессии проверяемой модели,
Найденная математическая модель адекватна, если дисперсии адекватности
и сравнивают ее с табличным значением F -распределения Из таблиц F -распределения при уровне значимости q и числах степеней свободы При равномерном дублировании
где Тогда
Проверку адекватности выполняют по формуле (5.9). Если же проверяемая модель оказалась неадекватной, необходимо: 1) ввести в математическую модель эффекты взаимодействия; 2) перейти к квадратичной модели, ввести 3) провести эксперимент повторно, уменьшив при этом интервалы варьирования. Рассмотренный метод проверки адекватности имеет физический смысл. В основе этой процедуры лежит проверка гипотезы об однородности дисперсии адекватности и дисперсии, характеризующей ошибку экспери-мента. Заметим, что дисперсия адекватности характеризует расхождения между результатами эксперимента При отсутствии дублированных опытов эффективность регресс-сионной модели оценивают следующим образом. Находят оценку дисперсии относительного среднего значения отклика:
где рассчитывают остаточную дисперсию:
вычисяют отношение
Величина Для эксперимента с дублированными опытами используется формула (5.10), а выражения для оценки дисперсий
где Значение
Анализ уравнения регрессии Пусть было получено адекватное уравнение регрессии, например
Проанализируем, какую информацию оно содержит. 1. 2. Выделение незначимых факторов по t -критерию Стьюдента. Фактор незначим, если он не оказывает существенного влияния на процесс. 3. Степень влияния каждого из факторов. Проранжировать факторы можно путем сравнения абсолютных величин коэффициентов уравнений регрессии: чем 4. Направление влияния каждого фактора на процесс (выходную величину). При этом обращается внимание на знак коэффициента регрессии. Знак (+) у коэффициента уравнения свидетельствует о том, что при увеличении значения фактора выходная величина растет. Знак (–) указывает, что при усилении значения данного фактора выходная величина убывает. Можно также интерпретировать роль парных взаимодействий, например 5. Величина 6. Уравнение регрессии в зависимости от натуральных значений факторов, для получения которого нужно воспользоваться формулой перехода (4.1). 7. Можно получить зависимость выходной величины в виде графиков как от каждого фактора, так и от их взаимодействий. Для этого удобнее использовать уравнение регрессии в нормализованных обозначениях факторов, положив все значения факторов, кроме одного, равными нулю. Например: Если уравнение регрессии адекватно, его можно использовать для интерпретации, т. е. для предсказания значений факторов внутри диапазона варьирования. Можно оптимизировать
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.006 с.) |

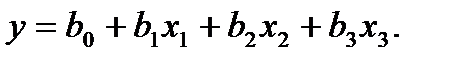 (5.6)
(5.6)  известны, то можно просто подсчитать расчетные значения
известны, то можно просто подсчитать расчетные значения  . С этой целью подставим в уравнение (5.6) значения факторов
. С этой целью подставим в уравнение (5.6) значения факторов  , соответствующие каждому из проведенных опытов. Если модель выбрана правильно, то
, соответствующие каждому из проведенных опытов. Если модель выбрана правильно, то 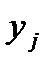 .
.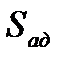 , характеризующую адекват-ность модели:
, характеризующую адекват-ность модели: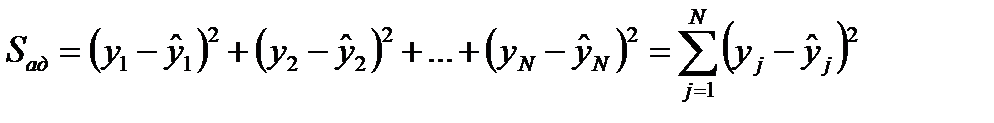 . (5.7)
. (5.7)  , полученные расчетом
, полученные расчетом 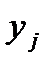 . Сумма квадратов
. Сумма квадратов 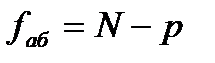 ,
,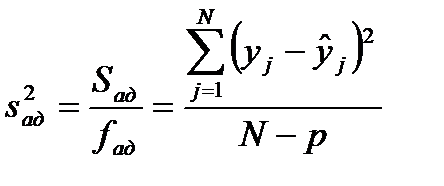 . (5.8)
. (5.8)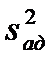 и воспроизводимости
и воспроизводимости 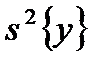 однородны. Для проверки адекватности вычисляют величину
однородны. Для проверки адекватности вычисляют величину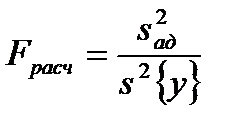 , (5.9)
, (5.9) .
.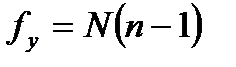 и
и 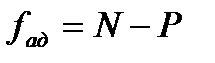 находят
находят 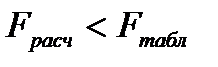 ,то проверяемая модель адекватна.
,то проверяемая модель адекватна.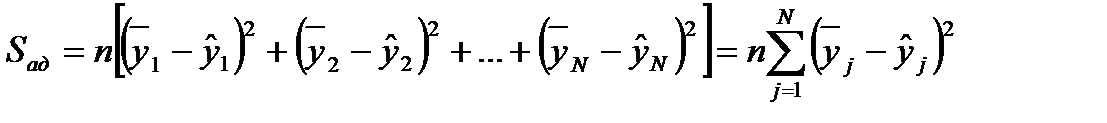 ,
,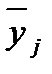 – усредненное по всем наблюдениям значение функции отклика
– усредненное по всем наблюдениям значение функции отклика  .
.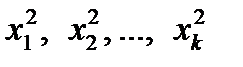 , т. е. рассмотреть другие планы;
, т. е. рассмотреть другие планы;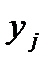 и значениями выходной величины
и значениями выходной величины 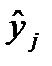 , вычисленными по уравнению регрессии. Логично принять, что модель удовлетворительно описывает объект исследования, т. е. является адекватной, если указанное расхождение вызвано только эксперимен-тальными ошибками, а не связано, например, с неудачным выбором математической модели. Проверка гипотезы об однородности рассматриваемых дисперсий п выясняет общность происхождения экспериментальных ошибок и расхождения между
, вычисленными по уравнению регрессии. Логично принять, что модель удовлетворительно описывает объект исследования, т. е. является адекватной, если указанное расхождение вызвано только эксперимен-тальными ошибками, а не связано, например, с неудачным выбором математической модели. Проверка гипотезы об однородности рассматриваемых дисперсий п выясняет общность происхождения экспериментальных ошибок и расхождения между 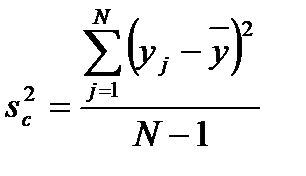 ,
,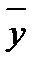 – среднее значение отклика по всем опытам,
– среднее значение отклика по всем опытам, 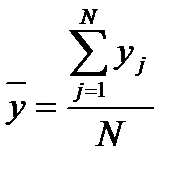 ;
;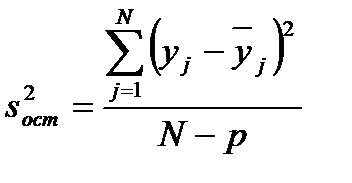 ;
; . (5.10)
. (5.10) 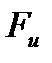 показывает, во сколько раз уравнение регрессии описывает результаты эксперимента точнее, чем простое среднее арифметическое, взятое по всем опытам. Регрессионная модель считается эффективной, если
показывает, во сколько раз уравнение регрессии описывает результаты эксперимента точнее, чем простое среднее арифметическое, взятое по всем опытам. Регрессионная модель считается эффективной, если 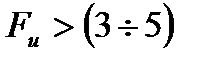 .
.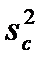 и
и 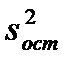 примут вид:
примут вид: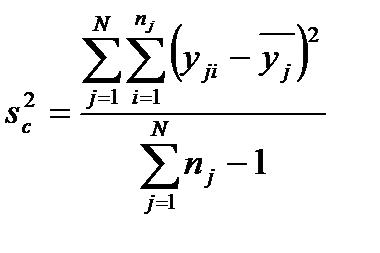 ;
;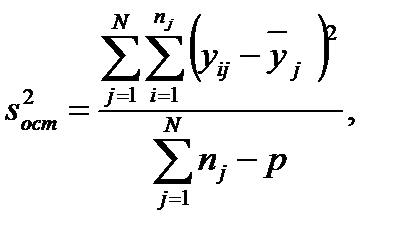
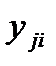 – значение отклика в i -м дублированном опыте j -й серии;
– значение отклика в i -м дублированном опыте j -й серии; 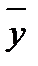 определяют по уравнению
определяют по уравнению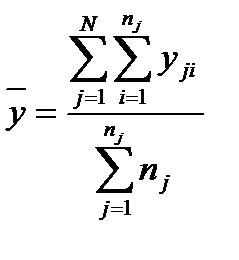 .
. 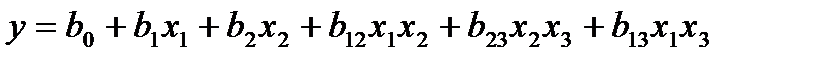 .
.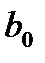 – среднее значение выходной величины.
– среднее значение выходной величины. больше, тем существеннее роль фактора при этом коэффициенте и тем сильнее его влияние на процесс.
больше, тем существеннее роль фактора при этом коэффициенте и тем сильнее его влияние на процесс.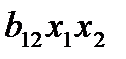 . Если
. Если 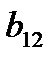 имеет знак (+), то выходная величина возрастает при одновременном возрастании или убывании факторов
имеет знак (+), то выходная величина возрастает при одновременном возрастании или убывании факторов 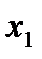 и
и 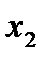 . Если
. Если 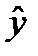 при различных значениях
при различных значениях 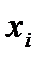 в диапазонах варьиро-вания факторов.
в диапазонах варьиро-вания факторов.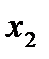 и
и 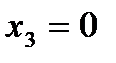 , получим
, получим  (можно положить
(можно положить 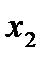
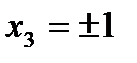 ).
).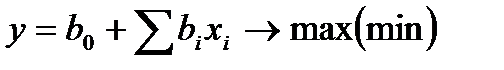 при
при 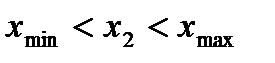 .
.


