
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы как объект исследованийСодержание книги
Поиск на нашем сайте
В.В. Шелгунов
Математические методы в Теплоэнергетике
Курс лекций
Тверь 2017 ВВЕДЕНИЕ В настоящее времяневозможно представить проведение научных исследований без широкого использования математических методов. Сущность этого методов познания окружающего мира и его составляющих состоит в замене исследуемого объекта абстрактным символом – математической моделью – и дальнейшем ее изучении В настоящее время математическое моделирование находится на Технические, экологические, информационные, экономические и другие системы на современном этапе развития науки уже не могут быть исследованы в необходимой полноте и точности традиционными теоретическими методами. Прямой натурный эксперимент над совре-менными системами в большинстве случаев является дорогостоящим, сложным, либо его проведение невозможно; цена ошибок и просчетов при этом недопустимо высока. Поэтому математическое моделирование является важным достижением и средством научно-технического прогресса. Технологические процессы (в т.ч. и применяемые в теплоэнергетике)– это сложные физико-химические системы, имеющие двойственную детерминированно-стохастическую природу, переменные в пространстве и времени. На каждой стадии процесса могут происходить явления переноса массы, энергии, импульса. Процесс в целом реализуется в оборудовании с определенными техническими характеристиками, оказывающими влияние на характер его протекания. При изученни дисциплины « Математические методы в теплоэнергетике» Рассматриваются основные принципы и методы создания математического описания технологических процессов, планирования исследований, обработки и анализа полученных результатов.
ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ Как уже было указано, математическое моделирование служит
Рис. 1.1. Структурные составляющие математической модели
Математические модели технологических процессов можно кратко классифицировать следующим образом: 1) простые и системные (по сложности объекта моделирова- 2) линейные, нелинейные (по оператору модели); 3) описывающие состояние и поведение совокупности тех или иных параметров объекта: управляемых входных, неуправляемых входных внешних, внутренних (собственных), выходных; 4) дискретные (описательные), оптимизационные, управленческие Процесс математического моделирования включает в себя: составление математического описания изучаемого объекта (выявле-ние сущности описываемого объекта, выбор теоретических известных закономерностей, пригодных для описания объекта, выбор числа определяющих параметров; выбор метода решения математического описания и возможности его реализации – аналитические способы, численные методы, использование прикладных программ ЭВМ и т. п.; установление соответствия (адекватности) модели объекту – сравне-ние результатов измерений с рассчитанными по модели; Все этапы математического моделирования являются взаимо-связанными и должны корректироваться с целью соответствия друг
Таблица 1.1. Классификация систем
Рис. 1.3. Схема обратной связи Обратные связибывают положительными и отрицательными. Обратная связь, увеличивающая влияние входного воздействия на выходную величину системы, называется положительной; уменьшающая это влияние – отрицательной. Отрицательная обратная связь способствует восстановлению Одним из наиболее важных понятий кибернетики является понятие «черного ящика», определяющего механизм управления системой. Для описания и моделирования кибернетических систем, а также
Рис. 1.4. Схема исследований объекта Таким образом, «черным ящиком» будем называть систему, в которой для наблюдения доступны лишь входные и выходные величины,
Общие сведения Целью большинства экспериментальных исследований в промыш-ленности является изучение влияния различных воздействий на объект моделирования. Эти воздействия называют факторами. Факторы могут быть основными и побочными. Основные факторы участвуют в эксперименте. Одни из них варьируются при исследовании технологического процесса (варьируемые факторы). Другие стабилизируются на определенном уровне. Побочные, посторонние факторы желательно устранять, однако все побочные факторы устранить невозможно. Поэтому результат единичного измерения представляет собой случайную величину, которая в результате опыта может принимать то или иное значение, причем заранее неизвестно, какое именно. Результат измерения по той же причине всегда отличается Случайная величина, принимающая отдельные друг от друга значения, которые можно пронумеровать, называется дискретной. Случайную величину, возможные значения которой непрерывно запол-няют некоторый промежуток, называют непрерывной. Отклонение результата измерения от истинного результата называется ошибкой Наряду с систематическими в любом эксперименте присутствуют случайные ошибки, обусловленные действием многочисленных факторов, причины возникновения которых неизвестны, а проявления нерегулярны. Такие факторы (их называют случайными) по-разному сказываются Кроме систематических и случайных различают грубые ошибки, Опыты, проводимые в одинаковых условиях при постоянных значениях основных факторов, называются однородными. Однородность испытаний является одним из важнейших условий правильного применения статистических методов обработки наблюдений. Для обеспе-чения однородности опытов необходимо, чтобы каждая серия проводилась одними и теми же исследователями, на одной и той же установке, Таким образом, единичный опыт не может дать точного и ис-черпывающего представления о связи изучаемого явления с вызвавшими его обстоятельствами. Многократные наблюдения дают более надежный результат. И от того, насколько профессионально будут обработаны полученные результаты, зависит объективность, точность, надежность определения истинного значения измеряемой характеристики и, следо-вательно, правильность всех дальнейших заключений и выводов. Отсюда логически вытекает необходимость научного подхода к обработке результатов опытов, что и составляет предмет изучения математической статистики. Математическая статистика– это наука о математических методах обработки, систематизации и использовании результатов наблюдения
Таблица 2.1. Статистический ряд
График, построенный по данным статистического ряда, называют гистограммой. При построении гистограммы по оси абсцисс отклады- Пусть, например, в результате измерения шероховатости поверхно-сти деталей получено n = 140 значений высот неровностей разруше-
Таблица 2.2 Высоты неровностей разрушения
Из табл. 2.2 видно, что высота микронеровностей у изменяется
Таблица 2.3 Статистические интервалы
Изображенная на рис. 2.1 гистограмма соответствует статистическому ряду, приведенному в табл. 2.3. Поскольку сумма всех относительных частот составляет единицу, то площадь гистограммы также равна единице. С увеличением числа опытов Если одновременно с увеличением числа опытов n увеличивать Для случайных величин, имеющих разную природу, статистические распределения могут быть различными. Известны, например, распре-деления Пуассона, Пирсона, биноминальное и многие другие. Среди них существует распределение, называемое нормальным (или гауссовским), которое применяется наиболее часто и играет важную роль в теории вероятностей и математической статистике.
Рис. 2.1. Гистограмма распределения Рис. 2.2. Кривая плотности нормальногораспределения
Далее будем исходить из предположения, что результаты наблюдений свободны от систематических ошибок, а случайные ошибки (а значит, Коэффициент корреляции Во многих случаях целью экспериментальных исследований является установление и изучение зависимости между некоторыми величинами. Если каждая из них является случайной, то используют методы корреляционного анализа. Так, методами корреляционного анализа можно оценить степень взаимосвязи между пределом прочности материала Между двумя случайными величинами имеется статистическая связь, если при изменении одной из них меняется распределение другой. Для оценки статистической связи по данным эксперимента широко использу-ется выборочный коэффициент корреляции. Пусть проведено п наблюде-ний и в каждом из них определились значения параметров (признаков) х
По каждой из них найдем среднее арифметическое которую можно переписать в виде, более удобном для вычислений: При расчетах полезно иметь в виду, что выборочный коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения х и y. Коэффициент корреляции всегда лежит в пределах –1 и сравнивают ее с табличным значением t -критерия Стьюдента, найден-ным при выбранном уровне значимости q и числе степеней свободы
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА Основные сведения Планирование эксперимента – это постановка опытов по некоторой заранее составленной схеме, обладающей некоторыми оптимальными свойствами. При этом необходимо: стремиться к минимизации числа опытов; одновременно варьировать все факторы, определяющие протекание процесса по специальным алгоритмам (правилам); использовать математический аппарат, формализующий ряд действий экспериментатора; иметь четкую стратегию, позволяющей принимать обоснованные решения после каждой проведенной серии опытов. Таким образом, планирование эксперимента – это комплекс приемов, позволяющих исследователю оптимально поставить эксперимент, со-образуясь с целью исследования (со стремлением получить максимум информации) при необходимости экономить средства (число опытов), Планирование эксперимента базируется на кибернетическом подходе к объекту исследований. Для описания объекта исследований модели-рования используется неизвестная система (рис. 3.1), подверженная различным воздействиям.
Рис. 3.1. Схема описания объекта моделирования
Используя планирование эксперимента, исследователь априори (до постановки опыта) может назвать виды входных и выходных внешних воздействий, связанных с объектом исследований, но содержание «черного ящика» пока остается нераскрытым. При рассмотрении «черного ящика» различают два основных вида параметров: входные управляемые Выходные параметры часто называют параметрами оптимизации, целевыми функциями, выходными величинами и т. д.
6.2. Назначение планирования эксперимента Требования, предъявляемые к варьируемым факторам 1. Управляемость. Фактор является управляемым, если исследователь имеет воз-можность задавать нужное значение данного фактора в диапазоне варьирования и поддерживать его постоянным в течение всего отдельного опыта. Каждый фактор должен быть точной характеристикой определенного воздействия на объект исследований, которым можно управлять. Эксперименты, проводимые с управляемыми факторами, называются активными. 1. Независимость. 2. Данное требование означает возможность устанавливать 3. Однозначность. Факторы должны непосредственно воздействовать на процесс 4. Совместимость. Все комбинации факторов, возможные при планировании и про-ведении эксперимента, должны быть реализуемы на практике и безопасны. При несовместимости факторов часто приходится переформулировать постановку задачи исследований, исключать некоторые из факторов 5. При наличии качественных факторов принимается одно из ре-шений: а) проводить исследование отдельно для каждого фактора,
6.4.2. Нормирование обозначений варьируемых факторов Рассмотрим многофакторные планы (эксперименты), когда на объект исследований воздействуют сразу несколько (k) факторов; в натуральных обозначениях запишем Пусть некоторый фактор
Следовательно, нижнему уровню фактора соответствует значение Выбор регрессионной модели Как уже отмечалось, под математической моделью подразумевается вид функции отклика
Выбрать модель – значит выбрать вид этой функции, записать Для того чтобы выбрать одну из множества разнообразных Если несколько различных моделей отвечают нужным требованиям, то следует выбрать ту из них, которая является самой простой. Логарифмическая функция, представленная на рис. 3.3, на некото- В уравнении (3.6) b – коэффициент, который можно оценить, например, по результатам опытов. Какое из уравнений проще – (3.5)
Выпишем полиномы для случая двух факторов, различающиеся
Итак, мы представили неизвестную нам функцию полиномом. Операция замены одной функции другой, в каком-то смысле эквивалентной функцией называется аппроксимацией. Следовательно, мы аппроксимировали неизвестную нам функцию полиномом. Эксперимент необходим для получения численных значений коэффициентов поли-номов, и чем больше коэффициентов, тем больше опытов нужно поставить, что само по себе затруднительно. Поэтому следует найти полином, содержащий как можно меньше коэффициентов и при этом удовлетворяющий требованиям, предъявляемым к модели. При заданном числе факторов чем ниже степень полинома, тем меньше в нем коэффициентов. Нужно, чтобы модель предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называют градиентом. В этом случае лучше использовать полином первой степени, так как он содержит информацию о направлении градиента и минимальное число коэффициентов при данном числе факторов. Единственное опасение заключается в том, всегда ли линейная модель будет адекватна. Однако почти у любой точки имеется такая окрестность, Кроме задачи оптимизации, возникает задача построения математической модели, когда нужно предсказать результат с требуемой точностью во всех точках некоторой заранее заданной области. С этой целью последовательно увеличивают степень полинома до тех пор, пока модель не окажется адекватной. Таким образом, на первой стадии экспериментальных исследований при отсутствии сведений о модели разумно выбирать модель первогo порядка. Если же есть сведения о нелинейности, то принимается модель второго порядка. После выбора модели определяется диапазон варьирования факторов (D), который во всех случаях должен быть не шире, чем область опре-деления факторов (О), т. е. D Особое внимание следует уделить выбору центра эксперимента (нулевой точки). Желательно, чтобы она была в области оптимума или как можно ближе к ней, тогда ускоряется поиск оптимальных решений. Если имеются сведения о значении параметра оптимизации по результатам предшествующих исследований, то за нулевую точку принимается та, При выборе интервала варьирования следует исходить из того, Следует учитывать: точность фиксирования факторов – чем она меньше, тем больше должен быть интервал варьирования; кривизну поверхности откликов – при большей кривизне следует сужать интервал варьирования; диапазон изменения параметра оптимизации в различных точках – чем он уже (в сравнении с его изменением в повторных опытах), тем шире должен быть интервал варьирования. 6.6. Основные виды планов эксперимента В настоящем параграфе рассматриваются особеннос
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.218.180 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


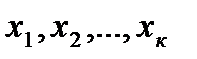 ящика, и воздействиями
ящика, и воздействиями 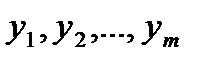 на его выходе (рис. 1.4)
на его выходе (рис. 1.4)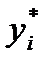
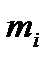
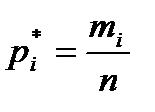
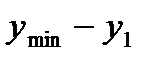
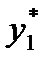
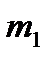
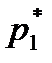
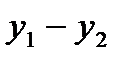
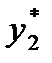
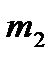
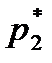
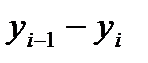
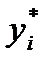
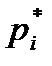
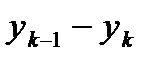
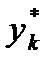
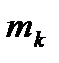
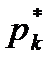
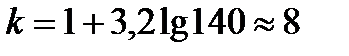 . Результаты подсчета значений
. Результаты подсчета значений 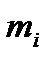 и относительных частот
и относительных частот 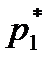 приведены в четвертом
приведены в четвертом 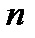 значение каждой частоты становится все ближе к соответствующей вероятности
значение каждой частоты становится все ближе к соответствующей вероятности 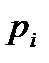 . Это утверждение, выражающее требование статистической устойчивости частот, является важнейшей предпосылкой применения статистических методов.
. Это утверждение, выражающее требование статистической устойчивости частот, является важнейшей предпосылкой применения статистических методов.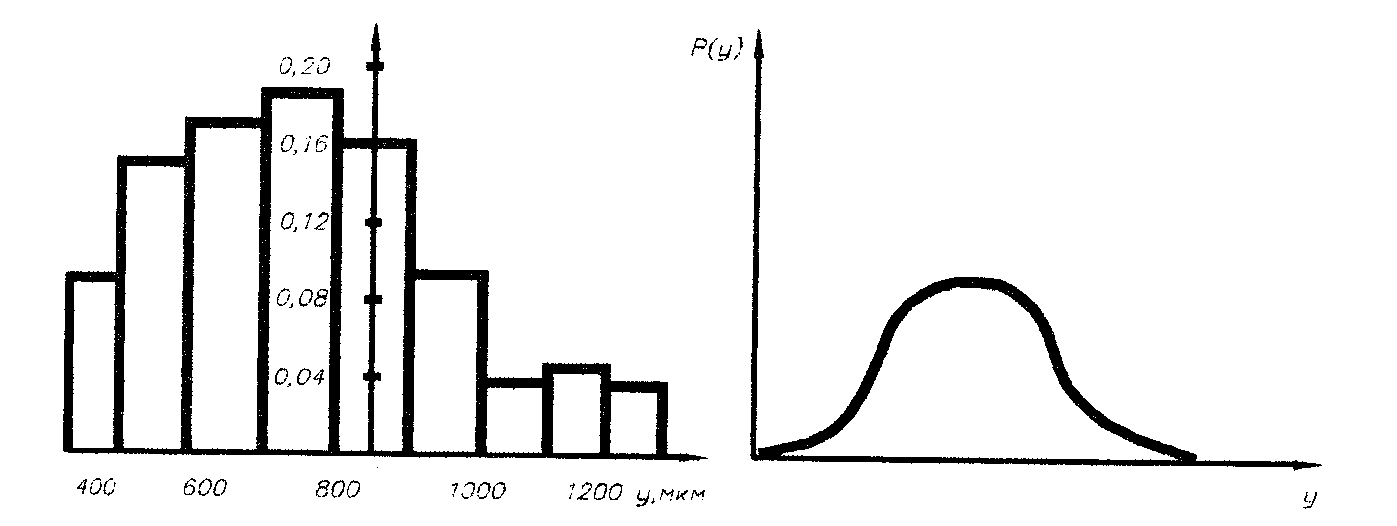
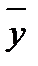 и
и 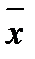 , а также выборочный стандарт
, а также выборочный стандарт 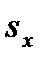 и
и 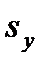 . Выборочный коэффициент корреляции r рассчитывается по формуле
. Выборочный коэффициент корреляции r рассчитывается по формуле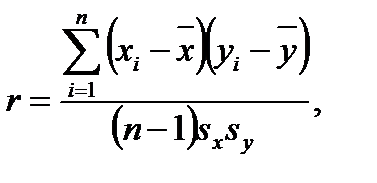 (2.26)
(2.26)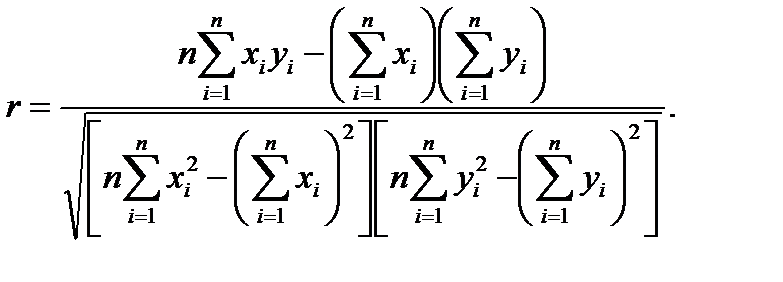 (2.27)
(2.27)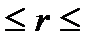 1
1 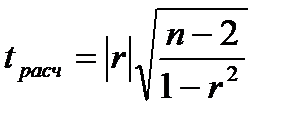 (2.28)
(2.28)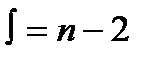 . Если
. Если 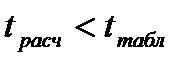 принимается гипотеза о некоррелированности величин х и у. В противном случае коэффициент корреляции значимо отличается от нуля, т. е. между величинами х и у существует линейная статистическая связь.
принимается гипотеза о некоррелированности величин х и у. В противном случае коэффициент корреляции значимо отличается от нуля, т. е. между величинами х и у существует линейная статистическая связь.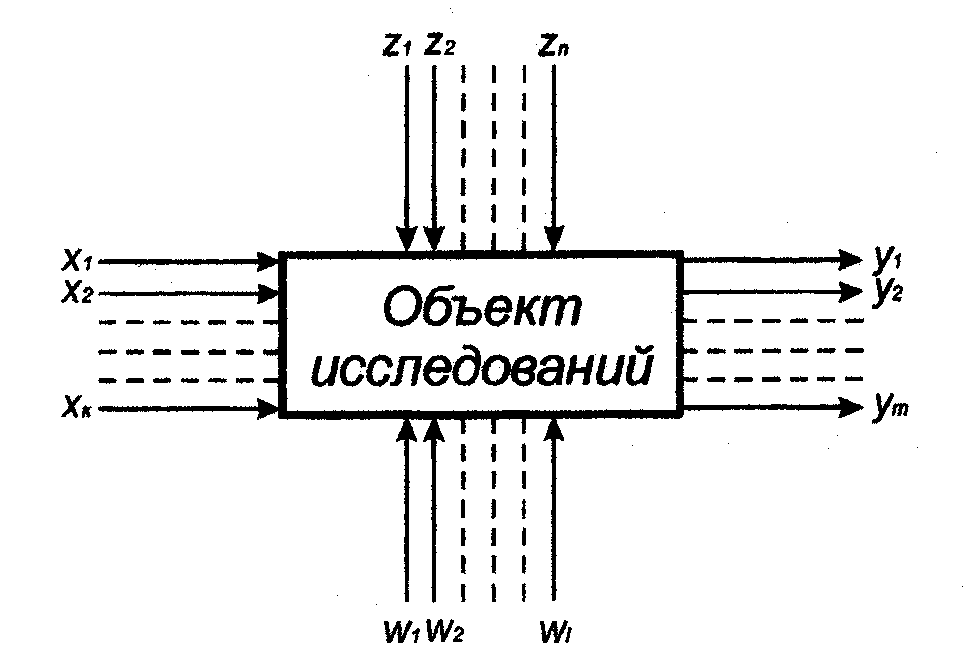
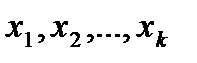 ) и выходные (
) и выходные (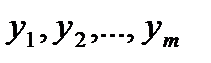 ). Некоторые из них могут быть приняты в качестве критериев оптимизации. Кроме того, на объект воздействуют неуправляемые параметры. Одни из них (
). Некоторые из них могут быть приняты в качестве критериев оптимизации. Кроме того, на объект воздействуют неуправляемые параметры. Одни из них (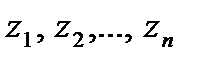 ) могут контролироваться в процессе постановки опытов без их целе-направленного изменения, другие (
) могут контролироваться в процессе постановки опытов без их целе-направленного изменения, другие (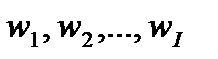 ) являются неконтроли-руемыми (из-за недостатка информации) и относятся к возмущающим воздействиям.
) являются неконтроли-руемыми (из-за недостатка информации) и относятся к возмущающим воздействиям.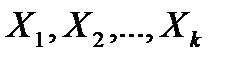 .
.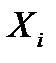 варьируется в диапазоне
варьируется в диапазоне 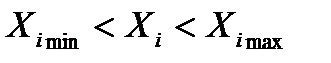 . Основной уровень варьирования
. Основной уровень варьирования 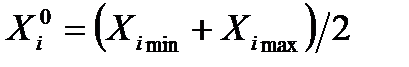 . Для упрощения записи условий эксперимента и обработки данных имеет смысл перейти к безразмер-ным (нормализованным) обозначениям факторов, т. е. от
. Для упрощения записи условий эксперимента и обработки данных имеет смысл перейти к безразмер-ным (нормализованным) обозначениям факторов, т. е. от 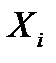 к
к 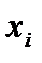 по формулам:
по формулам: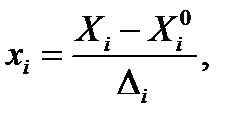 (3.4)
(3.4)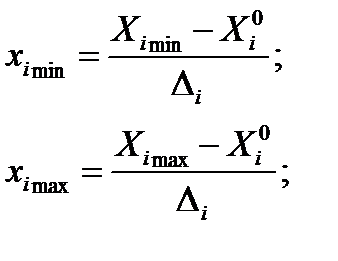
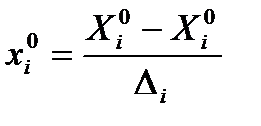 .
.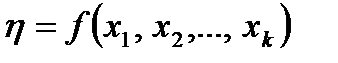 .
.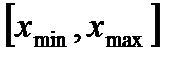 с достаточной точностью описывается уравне-ниями:
с достаточной точностью описывается уравне-ниями: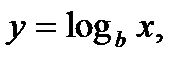 (3.5)
(3.5)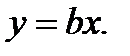 (3.6)
(3.6)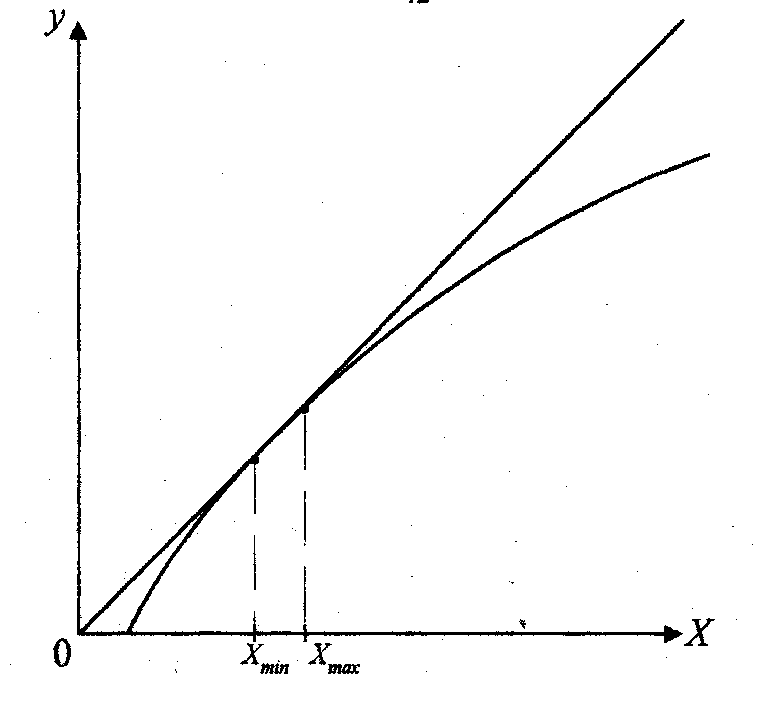
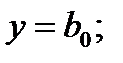 полином первой степени:
полином первой степени: 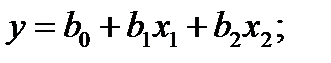 полином второй степени:
полином второй степени: 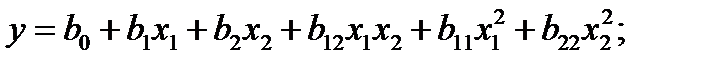 полином третьей степени:
полином третьей степени: 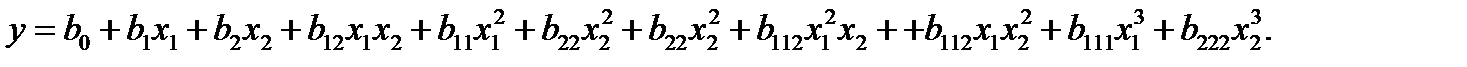
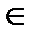 О.
О.


