
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор факторов и уровней их варьирования
После выбора параметров (критериев) оптимизации, выходной величины приступают к следующей стадии работы, заключающейся Фактор – это управляемая независимая переменная величина, Факторы могут быть количественными и качественными. Выбранные для эксперимента количественные и качественные состояния фактора называются уровнями его варьирования, т. е. значениями фактора в экс-перименте. Наименьшее значение, которое принимает данный фактор Пусть i – номер фактора,
Диапазон значений от Разность ∆ – интервал варьирования – рассчитывается по формулам:
Требования, предъявляемые к варьируемым факторам 1. Управляемость. Фактор является управляемым, если исследователь имеет воз-можность задавать нужное значение данного фактора в диапазоне варьирования и поддерживать его постоянным в течение всего отдельного опыта. Каждый фактор должен быть точной характеристикой определенного воздействия на объект исследований, которым можно управлять. Эксперименты, проводимые с управляемыми факторами, называются активными. 1. Независимость. 2. Данное требование означает возможность устанавливать
3. Однозначность. Факторы должны непосредственно воздействовать на процесс 4. Совместимость. Все комбинации факторов, возможные при планировании и про-ведении эксперимента, должны быть реализуемы на практике и безопасны. При несовместимости факторов часто приходится переформулировать постановку задачи исследований, исключать некоторые из факторов 5. При наличии качественных факторов принимается одно из ре-шений: а) проводить исследование отдельно для каждого фактора,
6.4.2. Нормирование обозначений варьируемых факторов Рассмотрим многофакторные планы (эксперименты), когда на объект исследований воздействуют сразу несколько (k) факторов; в натуральных обозначениях запишем Пусть некоторый фактор
Следовательно, нижнему уровню фактора соответствует значение Выбор регрессионной модели Как уже отмечалось, под математической моделью подразумевается вид функции отклика
Выбрать модель – значит выбрать вид этой функции, записать Для того чтобы выбрать одну из множества разнообразных
Если несколько различных моделей отвечают нужным требованиям, то следует выбрать ту из них, которая является самой простой. Логарифмическая функция, представленная на рис. 3.3, на некото- В уравнении (3.6) b – коэффициент, который можно оценить, например, по результатам опытов. Какое из уравнений проще – (3.5)
Выпишем полиномы для случая двух факторов, различающиеся
Итак, мы представили неизвестную нам функцию полиномом. Операция замены одной функции другой, в каком-то смысле эквивалентной функцией называется аппроксимацией. Следовательно, мы аппроксимировали неизвестную нам функцию полиномом. Эксперимент необходим для получения численных значений коэффициентов поли-номов, и чем больше коэффициентов, тем больше опытов нужно поставить, что само по себе затруднительно. Поэтому следует найти полином, содержащий как можно меньше коэффициентов и при этом удовлетворяющий требованиям, предъявляемым к модели. При заданном числе факторов чем ниже степень полинома, тем меньше в нем коэффициентов. Нужно, чтобы модель предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называют градиентом. В этом случае лучше использовать полином первой степени, так как он содержит информацию о направлении градиента и минимальное число коэффициентов при данном числе факторов. Единственное опасение заключается в том, всегда ли линейная модель будет адекватна. Однако почти у любой точки имеется такая окрестность,
Кроме задачи оптимизации, возникает задача построения математической модели, когда нужно предсказать результат с требуемой точностью во всех точках некоторой заранее заданной области. С этой целью последовательно увеличивают степень полинома до тех пор, пока модель не окажется адекватной. Таким образом, на первой стадии экспериментальных исследований при отсутствии сведений о модели разумно выбирать модель первогo порядка. Если же есть сведения о нелинейности, то принимается модель второго порядка. После выбора модели определяется диапазон варьирования факторов (D), который во всех случаях должен быть не шире, чем область опре-деления факторов (О), т. е. D Особое внимание следует уделить выбору центра эксперимента (нулевой точки). Желательно, чтобы она была в области оптимума или как можно ближе к ней, тогда ускоряется поиск оптимальных решений. Если имеются сведения о значении параметра оптимизации по результатам предшествующих исследований, то за нулевую точку принимается та, При выборе интервала варьирования следует исходить из того, Следует учитывать: точность фиксирования факторов – чем она меньше, тем больше должен быть интервал варьирования; кривизну поверхности откликов – при большей кривизне следует сужать интервал варьирования; диапазон изменения параметра оптимизации в различных точках – чем он уже (в сравнении с его изменением в повторных опытах), тем шире должен быть интервал варьирования.
6.6. Основные виды планов эксперимента В настоящем параграфе рассматриваются особенности, свойства
6.6.1. Полные факторные планы Экспериментальные планы, в которых реализуются все возможные сочетания уровней факторов, называются полными факторными планами (ПФП) и имеютсвоиособенности построения. 1. Каждый фактор в ПФП варьируется лишь на двух уровнях, которые нормируются: (–1) – нижний и (+1) – верхний уровень. 2. Общее число различных опытов в ПФП 3. По результатам ПФП в частности можно получить линейное уравнение регрессии Метод построения ПФП заключается в создании таблиц, содержащих нормализованные значения факторов и полученные в результате опытов величины параметров оптимизации. Например: для двух варьируемых факторов (k = 2) в нормализованных обозначениях (N =
Таблица 3.1. Матрица Таблица 3.2. Матрица планирования планирования эксперимента № 1 эксперимента № 2
Из таблиц видно, что значения (–1) и (+1) принимаются в разных возможных сочетаниях, т. е. все их комбинации различны. Геометрическое изображение ПФП:для планов с двумя факторами имеем координатную плоскость, по оси абсцисс которой отложены значения Точки этого плана (рис. 3.4) образуют вершины квадрата, центр которого совпадает с началом координат. Внутренность квадрата является областью варьирования нормали-зованных факторов. Точки этого же плана для натуральных значений факторов (рис. 3.5) представляют собой прямоугольник. В этих ко-ординатах область варьирования факторов представляет собой внутрен-ность прямоугольника. Для двух факторов все возможные сочетания факторов легко найти перебором.
Рис. 3.3. Область варьирования Рис. 3.4. Область варьирования в нормализованных значениях в натуральных значениях
В случае построения ПФП для любого числа факторов задача усложняется: вводится фиктивное значение фактора Рассмотрим два наиболее распространенных приема. Для этого составим две матрицы трехфакторного ПФП, которые представлены
Таблица 3.3. Матрица трехфакторного ПФП № 1
Таблица 3.4. Матрица трехфакторного ПФП № 2
Для упрощения расчетов необходимо следующее. 1. Чередование знаков факторов. Здесь в первом столбце табл. 3.3 знаки меняются поочередно, во втором столбце – через два, в третьем – через четыре, в четвертом – через восемь и т. д. по степеням 2. Использование правила перемежения столбцов плана. При по-строчном перемежении двух столбцов плана произведение единиц Запись ПФП громоздка. Для ее сокращения вводятся условные буквенные обозначения строк (см. табл. 3.3 и 3.4). Порядковые номера факторов ставятся в соответствие строчной букве латинского алфавита: Таким образом, план, приведенный в табл. 3.4, может быть записан так: (1), План, показанный в табл. 3.4, записывается следующим образом: Полный факторный план обладает следующими свойствами. 1. Симметричность относительно центра эксперимента. Сумма значений любого фактора для всех опытов в нормализованных обозначениях
2. Нормированность. Поскольку заданные значения факторов в плане (–1) и (+1), сумма квадратов значений каждого фактора по всем опытам в нормализованных обозначениях равна числу опытов (сумма квадратов элементов каждого столбца равна числу опытов N), т. е. 3. Ортогональность. Скалярное произведение двух любых столбцов ПФП
4. Ротатабельность. Точки в ПФП подбираются так, что точность значений параметра процесса одинакова на равных расстояниях от центра эксперимента . 6.6.2. В-планы второго порядка Полные и дробные факторные планы позволяют получить линейное описание зависимости отклика от каждого из варьируемых факторов. Планами второго порядка называют такие планы многофактор-
В общем случае, когда число варьируемых факторов равно k, модель имеет следующий вид: Отметим, что планы, позволяющие получить линейную модель объекта, например, полные и дробные факторные планы, называют планами первого порядка. Регрессионные модели вида (3.11) называют, как уже отмечалось, моделями второго порядка, или квадратичными моделями. Число коэффициентов регрессии такой модели или Из выражения (3.11) видно, что реализация плана второго порядка позволяет описать зависимость выходной величины от каждого фактора в виде уравнения параболы. В планировании эксперимента синтез экспериментальных планов производится с позиций некоторого критерия, связанного с оценками параметров получаемой регрессионной модели. Так были построены ортогональные планы второго порядка, позволяющие получать статически независимые друг от друга оценки коэффициентов. Для этих планов матрица Однако требование ортогональности для планов второго порядка никак не связано с более естественным требованием получения наиболь-шей точности математической модели. Как известно, точность регресс-сионной модели определяется дисперсиями коэффициентов peгрессии С позиций перечисленных критериев наиболее простыми являются линейные модели. Полные и дробные факторные планы являются по от-ношению к этим моделям А -, G - и D -оптимальными, а также обладают свойствами ортогональности и ротатабельности. Вместе с тем построение D -оптимальных планов второго порядка для заданного числа опытов – еще не решенная задача. Вместе с тем известен ряд планов, близких к D -опти-мальным. Такими являются, в частности, рассматриваемые ниже В -планы второго порядка или планы типа В. Эти планы оказались весьма востребо-ваны исследователями-лесопромышленниками и деревообработчиками В В -планах второго порядка каждый фактор Назовем звездной точкой В -плана условия опыта, в котором один 1) 2) 3) 4) 5) 6) Очевидно, что при числе факторов k имеется 2 k различных звездных точек. В-план состоит из точек ПФП, к которым добавлено 2 k звездных точек. Таким образом, общее число опытов В -плана N =2 В табл. 3.5 и 3.6 приведены В -планы для k = 2 и k = 3. Опыты ПФП и ДФП, входящие в состав В -плана, обычно называют его opтoгональной частью. Связь нормализованных и натуральных обозначений факторов в В -плане задается формулой (4.1). Звездные точки 5...8, дополняющие ПФП до В -плана, расположены Из геометрического рассмотрения следует, что область варьирования факторов в В -плане (как и в ПФП и ДФП) является куб (гиперкуб) Кроме того, в области центра плана, т. е. при значениях факторов, близких к основному уровню, никаких опытов не ставится. Все опыты
Таблица 3.5. В-план для k = 2
Таблица 3.6 В-план для k = 3
Последнее обстоятельство может не удовлетворить исследователя, особенно в тех случаях, если построенная по результатам эксперимента модель служит для оптимизации объекта, например, для отыскания наилучших технологических режимов работы оборудования. При плани-ровании такого эксперимента исследователь выбирает обычно в качестве центра плана значения факторов, соответствующие наиболее типичным условиям протекания процесса. Поэтому описание объекта вблизи центра плана представляет наибольший интерес. В такой ситуации В -план может быть дополнен одним или несколькими опытами в центре плана, т. е. опытами, поставленными в условиях План второго порядка, содержащий в своем составе план Для построения регрессионной модели по результатам В -плана где b В формулах (3.14) обозначено: Дисперсии коэффициентов регрессии и ковариации между ними определяют по формулам: Рассмотрим случаи применения этих формул. 1. Отсутствие дублированных опытов (не считая опытов в центре плана). В этом случае N – число запланированных опытов. Например, для плана В 2. Равномерное дублирование. В этом случае формулы (3.7) и (3.8) Значения коэффициентов Т 1 ...Т 6 для В -планов с ПФП в орто-гональной части с числом факторов k = 2...5 при отсутствии опытов Таблица 3.7. Значения коэффициентов Т 1 ...Т 6 для В -планов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 называется центром эксперимента или основным уровнем (нулевой точкой).
называется центром эксперимента или основным уровнем (нулевой точкой). – i -й фактор, а
– i -й фактор, а  и
и  – минимальное
– минимальное  .
. до
до  называется диапазоном варьирования фактора в эксперименте или областью значений фактора
называется диапазоном варьирования фактора в эксперименте или областью значений фактора 

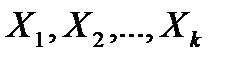 .
.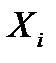 варьируется в диапазоне
варьируется в диапазоне 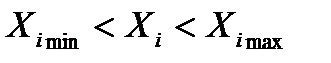 . Основной уровень варьирования
. Основной уровень варьирования 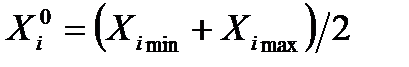 . Для упрощения записи условий эксперимента и обработки данных имеет смысл перейти к безразмер-ным (нормализованным) обозначениям факторов, т. е. от
. Для упрощения записи условий эксперимента и обработки данных имеет смысл перейти к безразмер-ным (нормализованным) обозначениям факторов, т. е. от 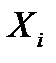 к
к 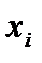 по формулам:
по формулам: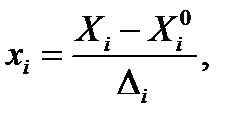 (3.4)
(3.4)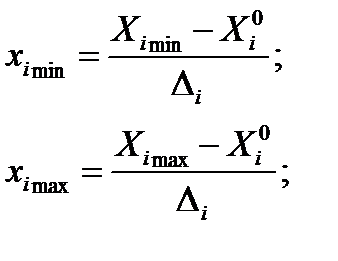
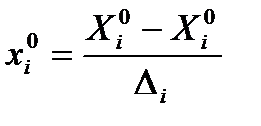 .
.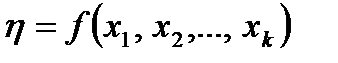 .
.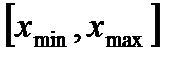 с достаточной точностью описывается уравне-ниями:
с достаточной точностью описывается уравне-ниями: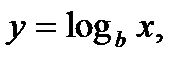 (3.5)
(3.5)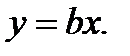 (3.6)
(3.6)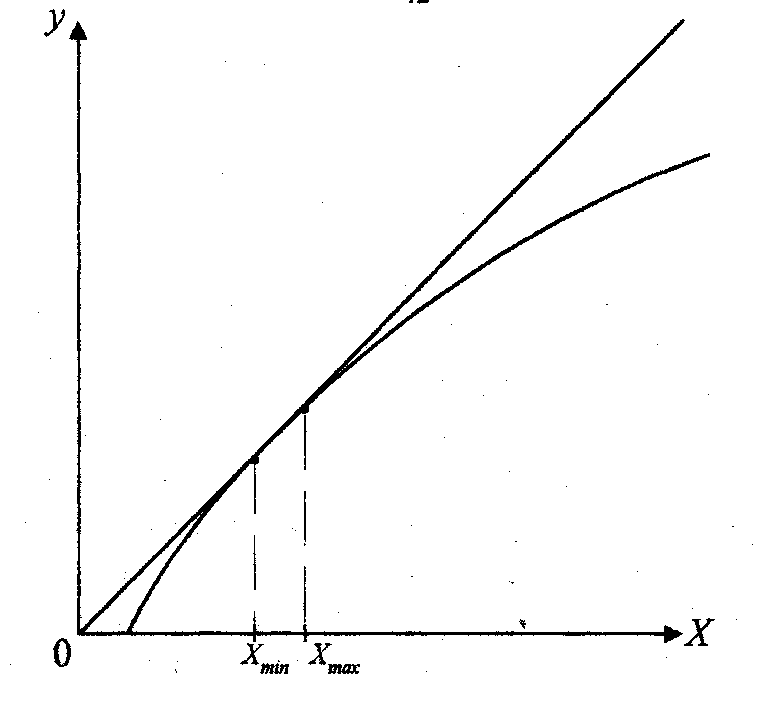
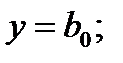 полином первой степени:
полином первой степени: 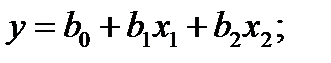 полином второй степени:
полином второй степени: 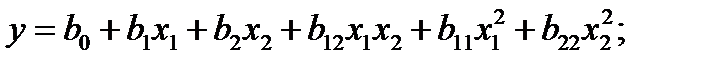 полином третьей степени:
полином третьей степени: 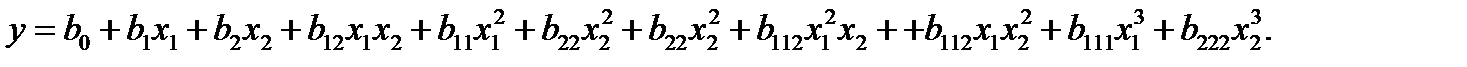
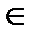 О.
О. , где k – число факторов; 2 – число уровней их варьирования.
, где k – число факторов; 2 – число уровней их варьирования. .
. ) составим таблицы (табл. 3.1 и 3.2), в которых строки соответствуют различным опытам, а столбцы – значениям факторов
) составим таблицы (табл. 3.1 и 3.2), в которых строки соответствуют различным опытам, а столбцы – значениям факторов 
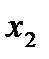
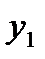
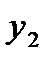


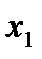 ,а по оси ординат – значения
,а по оси ординат – значения 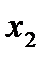 . Построим на этой плоскости точки, координаты которых соответствуют координатным значениям факторов в опытах 1, 2, 3 и 4 ПФП 2
. Построим на этой плоскости точки, координаты которых соответствуют координатным значениям факторов в опытах 1, 2, 3 и 4 ПФП 2  .
.
 для определения коэффициента регрессии
для определения коэффициента регрессии 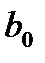 при i = 0 и используются некоторые правила алгебры матриц.
при i = 0 и используются некоторые правила алгебры матриц.

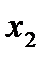


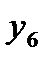


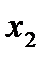
 и т. д., т. е. в строках находятся соответствующие факторы на верхнем уровне (+1). Например, в третьей строке табл. 3.4
и т. д., т. е. в строках находятся соответствующие факторы на верхнем уровне (+1). Например, в третьей строке табл. 3.4  , а в шестой – два фактора,
, а в шестой – два фактора,  , находятся на верхнем уровне, на что указывают обо-значения (ас).
, находятся на верхнем уровне, на что указывают обо-значения (ас). . (1) здесь обозначает, что все факторы находятся на нижнем уровне.
. (1) здесь обозначает, что все факторы находятся на нижнем уровне. .
. (3.7)
(3.7)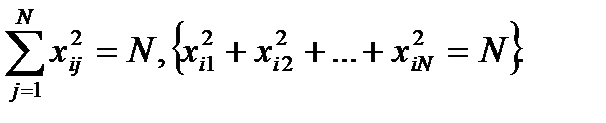 (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11)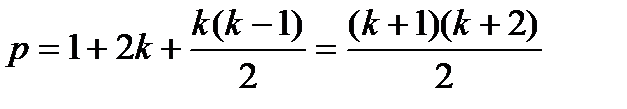 (3.12)
(3.12) (3.13)
(3.13) диагональна, и, следовательно, ковариации между всеми коэффициентами регрессии равны нулю:
диагональна, и, следовательно, ковариации между всеми коэффициентами регрессии равны нулю:  при i
при i 
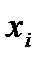 варьируется на трех уровнях, т. е. принимает в каждом опыте одно из трех значений: наименьшее
варьируется на трех уровнях, т. е. принимает в каждом опыте одно из трех значений: наименьшее 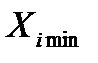 , наибольшее
, наибольшее  и среднее
и среднее  .
.  ;
; ;
; ;
; ;
; ;
; .
. +2 k.
+2 k.  5 можно построить разновидность
5 можно построить разновидность 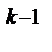 и добавив к ней 2 k звездных точек. Такой план, называемый В -планом с полурепликой, содержит N = 2
и добавив к ней 2 k звездных точек. Такой план, называемый В -планом с полурепликой, содержит N = 2  опытов. Так, для k = 5 В -план с ПФП содержит
опытов. Так, для k = 5 В -план с ПФП содержит  опыта,
опыта,  опытов.
опытов.












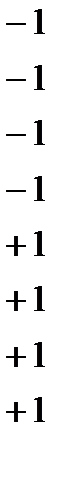

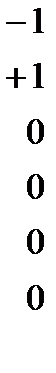
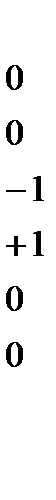

 . Эти опыты улучшают точность модели в окрестности центра плана. Кроме того, повторяющиеся опыты в центре плана, дают возможность оценить дисперсию воспроизводимости в том случае, если остальные опыты плана не дублируются. Построенный план является еще одной разновидностью В -плана.
. Эти опыты улучшают точность модели в окрестности центра плана. Кроме того, повторяющиеся опыты в центре плана, дают возможность оценить дисперсию воспроизводимости в том случае, если остальные опыты плана не дублируются. Построенный план является еще одной разновидностью В -плана. (3.14)
(3.14) – свободный член;
– свободный член;  . — линейные коэффициенты регрессии, i = 1, 2,..., k;
. — линейные коэффициенты регрессии, i = 1, 2,..., k; 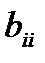 , – квадратичные коэффициенты регрессии, i = 1, 2,..., k;
, – квадратичные коэффициенты регрессии, i = 1, 2,..., k;  , – коэффициенты при парных взаимодействиях; i
, – коэффициенты при парных взаимодействиях; i 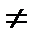 и; Т i – коэф-фициенты, значения которых указаны ниже.
и; Т i – коэф-фициенты, значения которых указаны ниже. (3.15)
(3.15)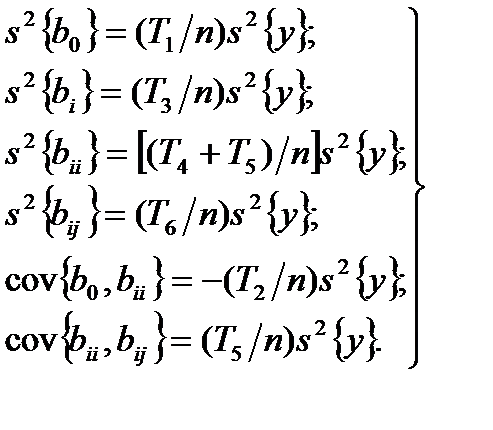 (3.16)
(3.16)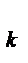 сПФП в ортогональной части и с
сПФП в ортогональной части и с  опытами в центре плана
опытами в центре плана 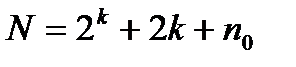 ;
;  – результаты j -го опыта, j = 1, 2,..., N. Величина n
– результаты j -го опыта, j = 1, 2,..., N. Величина n 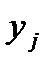 понимается среднее арифметическое по результатам j -й серии дублированных опытов; N – число серий дублированных опытов.
понимается среднее арифметическое по результатам j -й серии дублированных опытов; N – число серий дублированных опытов.



