
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение метода наименьших квадратов для получения уравнения регрессии выше первого порядкаСодержание книги
Поиск на нашем сайте
При составлении системы нормальных уравнений для полиномов выше первого порядка нелинейные члены уравнения регрессии рассматриваются как самостоятельные переменные. Рассмотрим пример решения для двух факторов. Для отыскания в уравнении
Таблица 4.2. План эксперимента
Система нормальных уравнений для регрессионной модели второго порядка
Решая совместно систему уравнений (4.6), найдем численные значения коэффициентов регрессии
7.4. Применение метода наименьших квадратов Для ортогональных планов решение системы нормальных уравнений настолько упрощается, что не требуется ЭВМ. Рассмотрим это на примере линейной модели с тремя факторами
Таблица 4.3. Матрица планирования ПФП
Выведем формулы для расчета коэффициентов регрессии. Отметим, что в матрице (см. табл. 4.1) i = 0, 1, 2, 3 (k) j = 1, 2, 3,..., 8 (N).
Используя свойство нормированности
Из системы (4.8) получим формулы для расчета коэффициентов регрессии
или в общем виде
Раскроем формулу (4.9) применительно к матрице ПФП для трех факторов (k = 3) при x
Поскольку
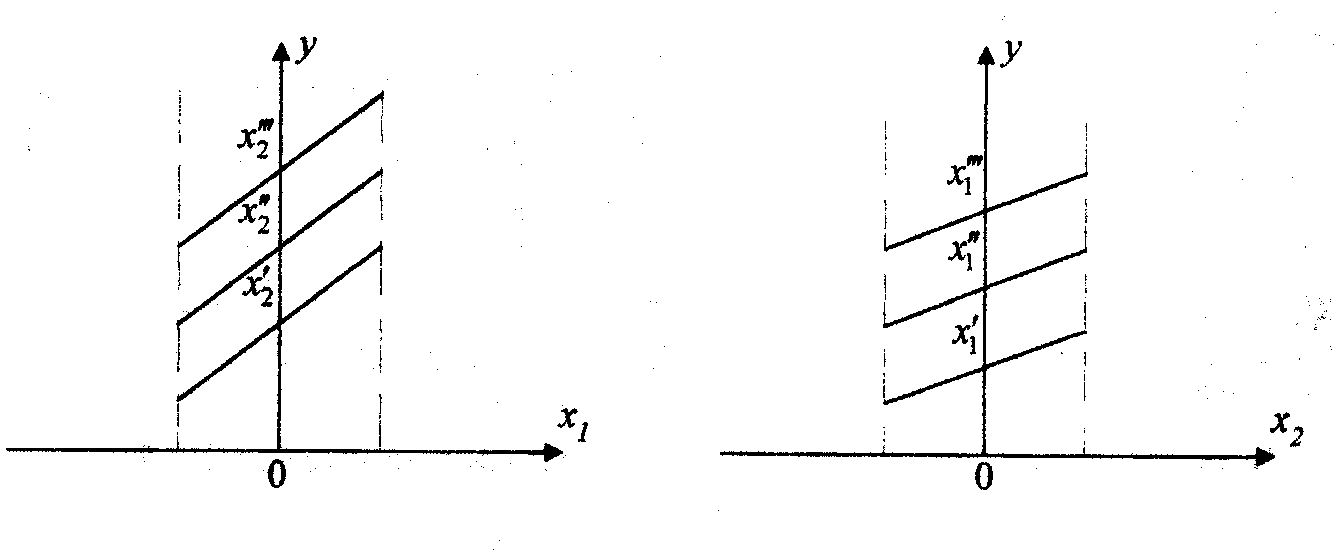
Нормализация факторов сводит расчет коэффициентов регрессии Графическая интерпретация модели представлена на рис. 4.1.
а б
Рис. 4.1. Значения параметра оптимизации:
Коэффициенты при независимых переменных указывают на степень влияния факторов при этих коэффициентах: чем больше абсолютная численная величина коэффициента, тем сильнее влияние, оказываемое фактором при этом коэффициенте. Если коэффициент имеет знак (+), В связи с наличием парных и более высоких взаимодействий факторов модель может быть неадекватна.
Эффекты взаимодействия Полный факторный план позволяет количественно оценить эффекты взаимодействия. Парное взаимодействие может быть получено перемноже-нием соответствующих столбцов значений факторов и последующим введением в матрицу эксперимента дополнительного фактора (табл. 4.4).
Таблица 4.4. Матрица ПФП при учете эффекта
Полученной матрице присущи три основных свойства ПФП, следовательно, уравнение с парным взаимодействием правомерно. Коэффициент регрессии парного взаимодействия подсчитывается по формулам:
или Построим в качестве примера матрицу базисной функций ПФП для
Таблица 4.5. Матрица базисной функции ПФП для N =
3десь В дальнейшем будем называть взаимодействия второго, третьего, четвертого и т. д. порядка соответственно: двойным, тройным (
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.008 с.) |

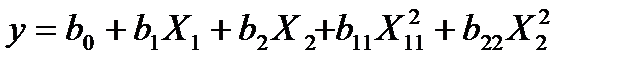 коэффициентоврегрессии
коэффициентоврегрессии 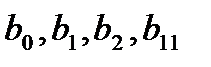 и
и 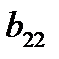 составим систему нормальных уравнений для плана эксперимента (табл. 4.2).
составим систему нормальных уравнений для плана эксперимента (табл. 4.2).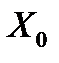
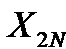
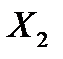
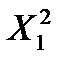
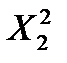
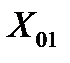
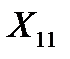
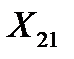
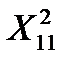
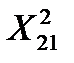
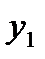
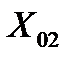
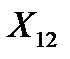
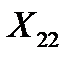
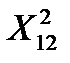
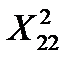
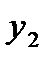
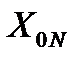
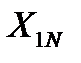
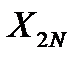
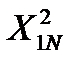
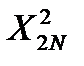
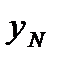
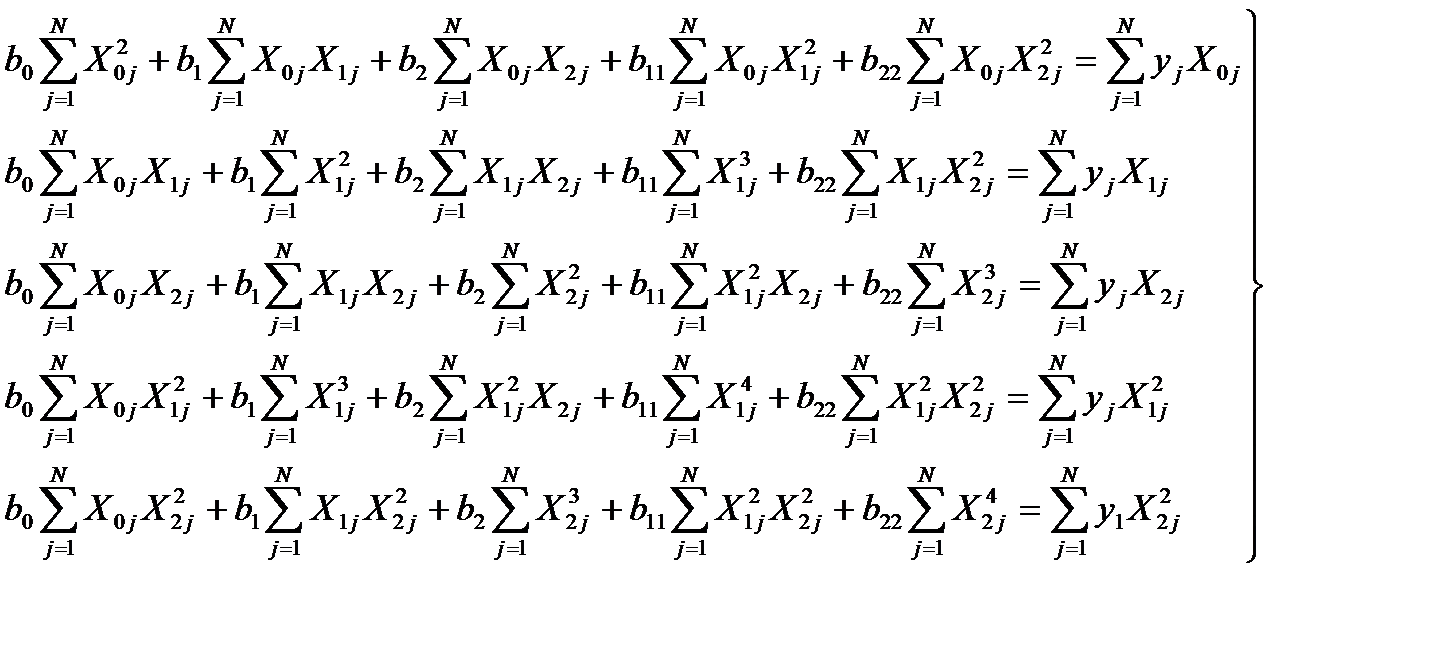 . (4.6)
. (4.6)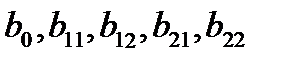 .
.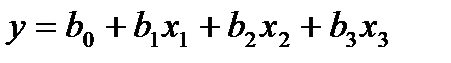 . Матрица планирования ПФП представлена в табл. 4.3.
. Матрица планирования ПФП представлена в табл. 4.3.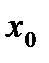
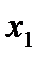
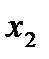
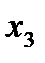
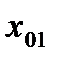
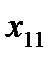
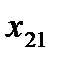
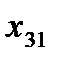
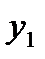
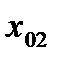
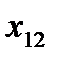

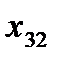
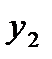
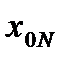
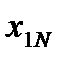
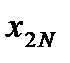
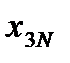
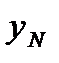
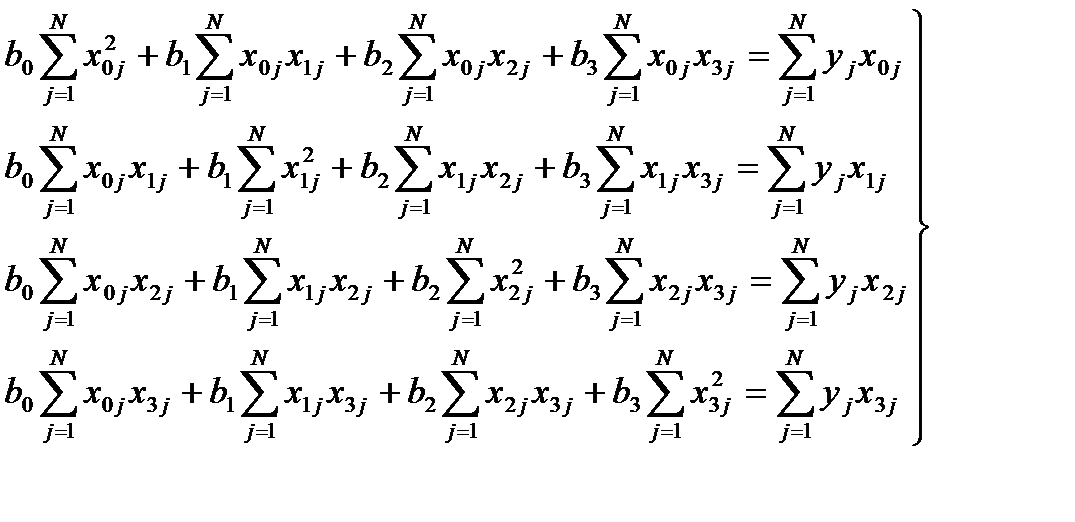 . (4.7)
. (4.7)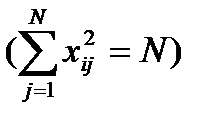 и свойство ортогональности
и свойство ортогональности  вместо системы уравнений (4.7)
вместо системы уравнений (4.7) 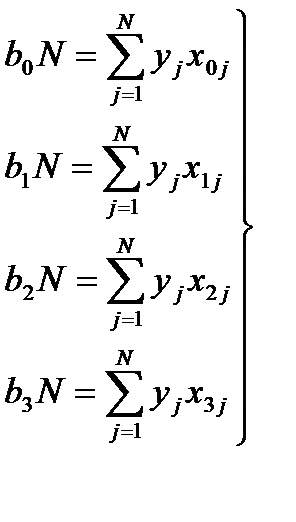 . (4.8)
. (4.8)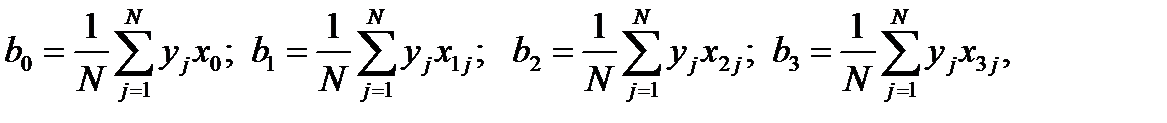
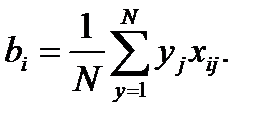 (4.9)
(4.9) = l:
= l: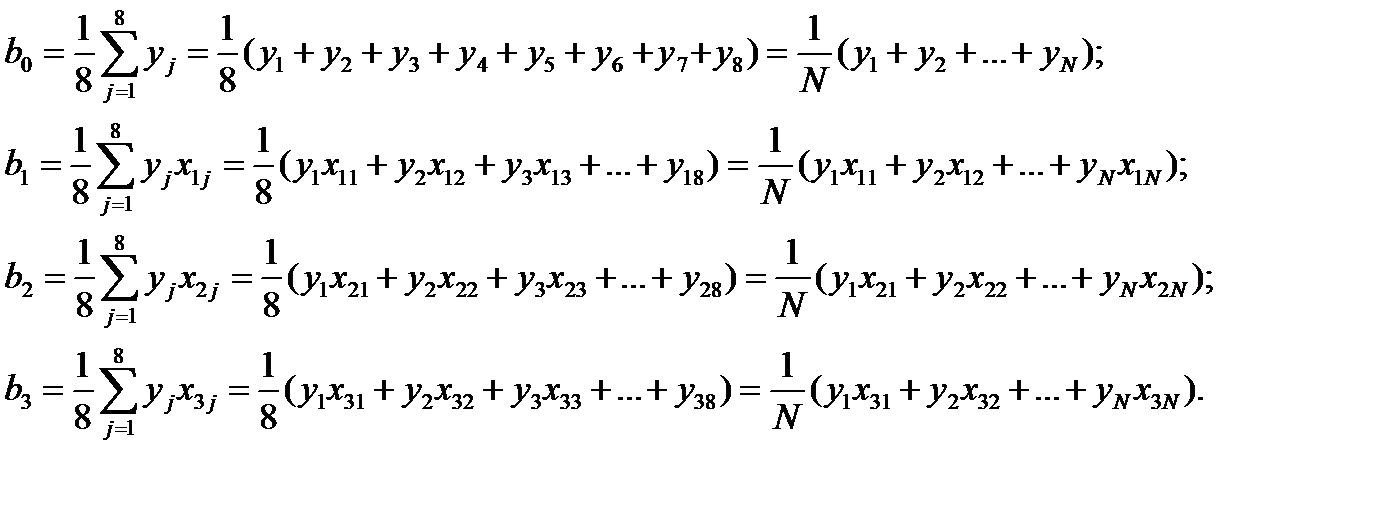
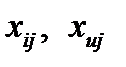 равны +1 или –1, имеем:
равны +1 или –1, имеем: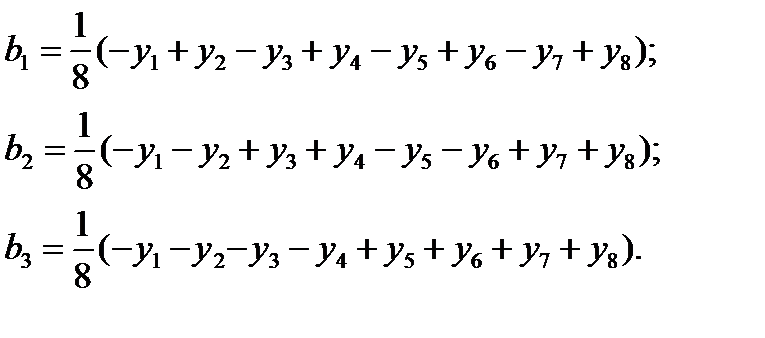
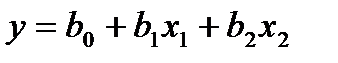 .
.
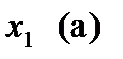 ; при фиксированном значении
; при фиксированном значении 
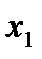
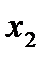
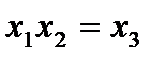
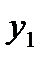
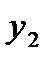
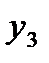
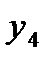
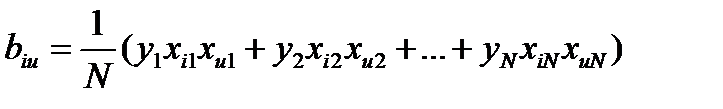
 . (4.10)
. (4.10)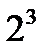 (табл. 4.5) и напишем соответствующее уравнение регрессии:
(табл. 4.5) и напишем соответствующее уравнение регрессии: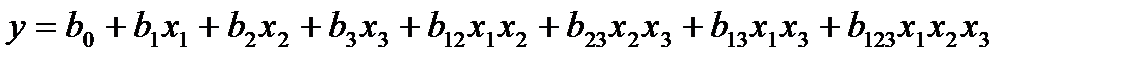 .
.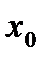
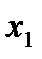

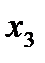
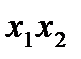
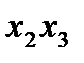
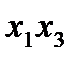
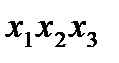

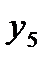
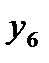
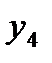
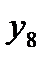
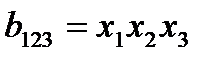 – тройное взаимодействие. Имеем восемь опытов
– тройное взаимодействие. Имеем восемь опытов 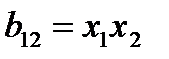 ).
).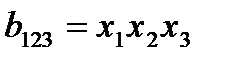 ),четверным (
),четверным (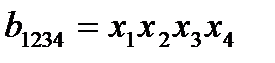 ) и т. д. Полный факторный план позволяет оценить взаимодействия любого порядка (двойное, тройное и т. д.).
) и т. д. Полный факторный план позволяет оценить взаимодействия любого порядка (двойное, тройное и т. д.).


