
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент регрессии тройного взаимодействияСодержание книги
Поиск на нашем сайте
Следует иметь в виду, что число вычисленных коэффициентов должно быть меньше числа поставленных опытов, т. е. p < N. В этом случае план называется ненасыщенным. При р = N план называется насыщенным; при p > N – сверхнасыщенным. Проверку адекватности выполняют только для ненасыщенных планов. Число парных взаимодействий можно определить по формуле число взаимодействий любого порядка
Число коэффициентов регрессии определяют по формулам: а) для линейного уравнения
б) для неполного квадратного уравнения
в) для полного квадратного уравнения
Полные факторные планы применяются при k
Минимизация числа опытов Полный факторный план обладает избыточностью опытов при его использовании для получения линейной модели. Для k варьируемых факторов линейная модель содержит k + 1 коэффициент регрессии, например: Сократить число опытов N можно за счет той информации, которая Для уяснения принципа построения ДФП возьмем ПФП N = 2
Таблица 4.6. Полная матрица ПФП для двух факторов
Если априори известно, что в выбранных интервалах варьирования, процесс можно описать линейной моделью
что не должно нас смущать, так как у принятой модели все парные взаимодействия незначимы. Теперь для трех факторов вместо восьми опытов можно поставить лишь четыре. При этом ПФП не теряет своих основных свойств. Таким образом, для того чтобы сократить число опытов, нужно приписать новому фактору вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значения нового фактора в условиях опытов определяются знаками этого столбца. В частности,план, представленный в табл. 4.6, называется полу-репликой (
7.7. Дробные факторные планы различной дробности Применив ДФП (табл. 4.6) Объединив две полуреплики, получим ПФП 2' с раздельными оценками парных взаимодействий и линейных эффектов. Возьмем теперь матрицу базисных функций ПФП 2
Таблица 4.7. Матрица базисных функций ПФП 2
Если известно, что можно пренебречь некоторыми или всеми парными взаимодействиями, то получим из ПФП 2 ряд новых ДФП. Так, заменяя
т. е. насыщенный план, так как р = N. Теперь видим, что для обозначений ДФП, в которых п линейных эффектов приравнены к эффектам взаимодействия, целесообразно пользоваться условным обозначением 2
7.8. Разрешающая способность дробного факторного плана При построении ДФП 2
Таблица 4.8. Матрица эксперимента для ДФП 2
Символическое обозначение произведения столбцов, равное +1 или
так как
Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генератором. При построении Возьмем матрицу базисных функций ПФП 2
Таблица 4.9. Матрица ДФП 2
Полуреплика 2
Седьмая и восьмая полуреплики имеют максимальную разрешающую способность, так как совместные оценки здесь определяются соотношением
или
В результате имеем следующую систему оценок:
Таким образом, получим:
Следует помнить о смешивании парных взаимодействий. Например, План, представленный табл.4.9, является насыщенным, так как N = р = 8, поэтому проверить адекватность полученной модели не представляется возможным. Это можно выполнить, пренебрегая каким-либо взаимодей-ствием. Рассмотрим случай, когда ОК
Далее получим систему смешанных оценок
Очевидно, что план с ОК 7.9. Условия применения дробных факторных планов 1. Дробные факторные планы применяют для построения линейной модели. 2. Эффективность ДФП возрастает с увеличением числа факто- 3. Дробные факторные планы могут быть наиболее эффективно использованы, если удачно осуществлено смешивание линейных эффек-тов с эффектами взаимодействий. При условии значимости некоторых взаимодействий это смешивание должно быть более умелым. В таком случае следует использовать априорные сведения. 4. При построении ДФП необходимо вводить новый фактор взамен эффекта взаимодействий, которым можно пренебречь. 5. Реплики, позволяющие сократить число опытов в 2 m раз, где m = 1, 2, 3, 4..., называются регулярными. Они позволяют рассчитывать коэффициенты регрессии так же просто, как и ПФП. 6. При ДФП линейные эффекты смешиваются с эффектами взаимодействий. Для определения системы смешивания нужно знать ОК 7. Для получения генераторов, указывающих, какие линейные эффекты смешаны с взаимодействиями, необходимо умножить ОК
ОК будет 1= 8. Разрешающая способность выше у того ДФП, линейные эффекты которого смешаны с взаимодействиями наивысшего порядка. Линейные эффекты могут быть освобождены от парных взаимодействий использованием метода «перевала», который состоит
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

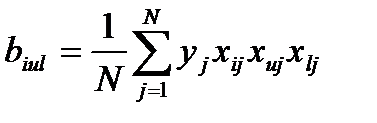 . (4.11)
. (4.11)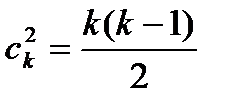 , (4.12)
, (4.12)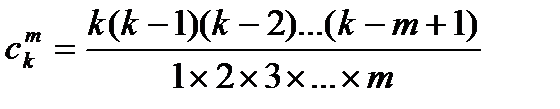 . (4.13)
. (4.13)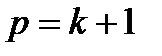 ; (4.14)
; (4.14)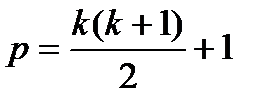 ; (4.15)
; (4.15)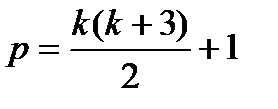 . (4.16)
. (4.16)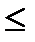 7. Число опытов
7. Число опытов 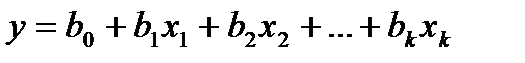 . Эксперимент, позволяющий отыскать эти коэффициенты и проверить адекватность ~3",: модели должен состоять из k + 2 = N
. Эксперимент, позволяющий отыскать эти коэффициенты и проверить адекватность ~3",: модели должен состоять из k + 2 = N  опытов. Так, для k = 4 N = 2
опытов. Так, для k = 4 N = 2  = 16, N
= 16, N 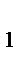 = k + 2 = 4 + 2 = 6,т. е. лишних десять опытов; для k = 6, N = 2
= k + 2 = 4 + 2 = 6,т. е. лишних десять опытов; для k = 6, N = 2 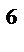 = 64, N
= 64, N 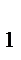 = К + 2 = 6 + 2 = 8,
= К + 2 = 6 + 2 = 8, 
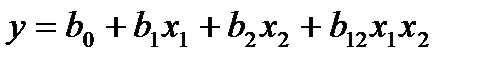 .
.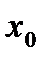
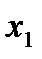
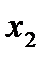
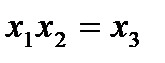
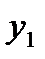
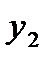
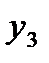
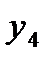
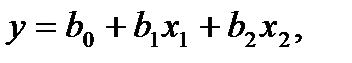 то достаточ-но определить три коэффициента. Останется одна степень свободы, которую можно употребить для минимизации числа опытов. При линей-ном приближении
то достаточ-но определить три коэффициента. Останется одна степень свободы, которую можно употребить для минимизации числа опытов. При линей-ном приближении 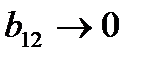
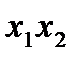 можно заменить новым фактором
можно заменить новым фактором 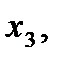 уровни варьирования которого будут соответствовать элементам столбца (x
уровни варьирования которого будут соответствовать элементам столбца (x 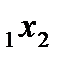 ).
). 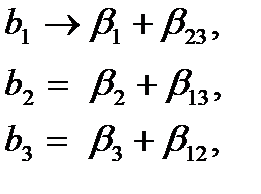
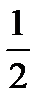 реплики) от ПФП 2
реплики) от ПФП 2 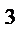 . Его обозначают 2
. Его обозначают 2 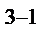 (3 – число факторов, а 1 указывает на то, что одно 3-1 взаимодействие заменяется новым фактором). При попытке определить столбцы произведений
(3 – число факторов, а 1 указывает на то, что одно 3-1 взаимодействие заменяется новым фактором). При попытке определить столбцы произведений 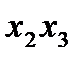
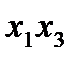 видим, что элементы столбца
видим, что элементы столбца 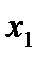 . Найденные нами коэффициенты будут оценками для совмест-ных элементов
. Найденные нами коэффициенты будут оценками для совмест-ных элементов 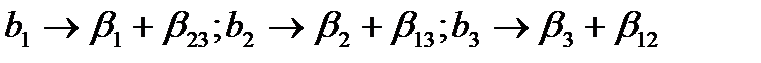 . Мы смешали эффекты взаимодействия с основными эффектами, но эффекты
. Мы смешали эффекты взаимодействия с основными эффектами, но эффекты 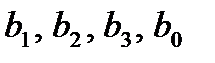 оценены раздельно друг от друга. Поскольку постулируется линейная модель,
оценены раздельно друг от друга. Поскольку постулируется линейная модель, 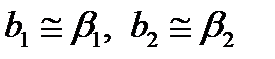 и
и 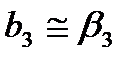 . Для большего числа факторов получение ДФП (т. е. минимизация числа опытов) сильно усложняется.
. Для большего числа факторов получение ДФП (т. е. минимизация числа опытов) сильно усложняется.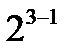 с четырьмя опытами, мы использовали половину ПФП 2
с четырьмя опытами, мы использовали половину ПФП 2 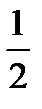 реплики). Приравняв
реплики). Приравняв 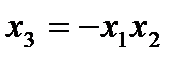 , можем получить вторую полуреплику от ПФП 2
, можем получить вторую полуреплику от ПФП 2 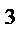 . В этом случае
. В этом случае 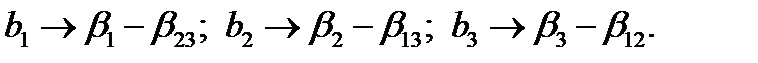
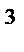 (табл. 4.7) и построим на ее основе ряд ДФП. Если пренебречь тройным взаимодействием
(табл. 4.7) и построим на ее основе ряд ДФП. Если пренебречь тройным взаимодействием 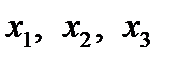 и вместо него поставить
и вместо него поставить 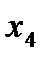 , получим полуреплику 2
, получим полуреплику 2 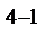 от ПФП 2
от ПФП 2 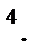
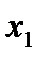
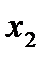
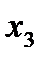
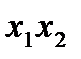
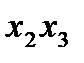
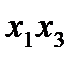
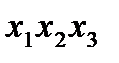
 на х
на х 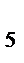 , получим
, получим 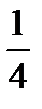 реплики от ПФП 2
реплики от ПФП 2 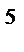 , которая обозначается
, которая обозначается 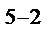 . Заменяя
. Заменяя 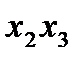 на
на 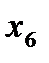 ,получим
,получим 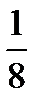 реплики 2
реплики 2 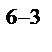 от ПФП 2
от ПФП 2 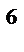 и, наконец, заменяя
и, наконец, заменяя 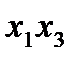 на
на 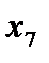 ,получим
,получим 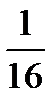 реплики 2
реплики 2 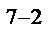 от ПФП 2
от ПФП 2 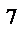 при N = 8 и k = 7. Таким образом, получаем уравнение вида
при N = 8 и k = 7. Таким образом, получаем уравнение вида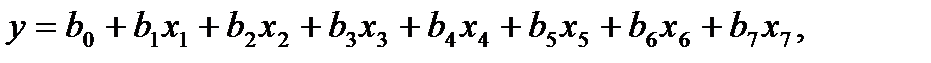
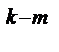
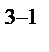 имеются две возможности приравнять
имеются две возможности приравнять 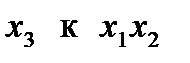 или
или 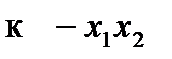 ,тогда получим матрицу эксперимента (табл. 4.8). Для произведения трех столбцов выполняется соотношение +1 =
,тогда получим матрицу эксперимента (табл. 4.8). Для произведения трех столбцов выполняется соотношение +1 = 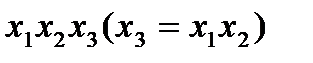 , т. е. для ДФП № 1 – (+1), а для ДФП № 2 –
, т. е. для ДФП № 1 – (+1), а для ДФП № 2 – 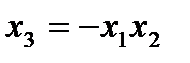 ).
).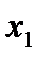
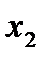
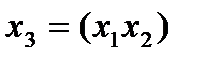
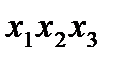
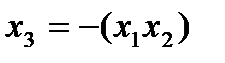
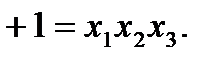 Тогда
Тогда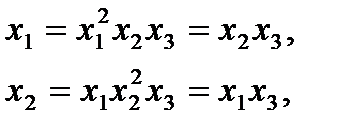
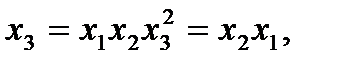
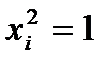 (всегда). Это значит, что для полуреплики 2
(всегда). Это значит, что для полуреплики 2 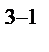 (№ 1) коэффициенты линейного уравнения будут оценками
(№ 1) коэффициенты линейного уравнения будут оценками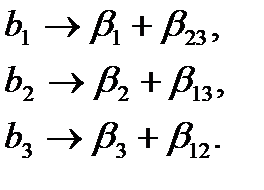
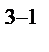 были использованы генерирующие соотношения
были использованы генерирующие соотношения 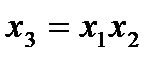 и
и 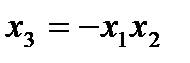 .
.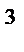 и построим ДФП 2
и построим ДФП 2 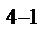
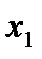
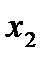
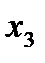
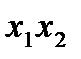
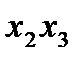

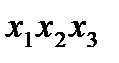
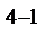 в этом случае имеет восемь вариантов:
в этом случае имеет восемь вариантов: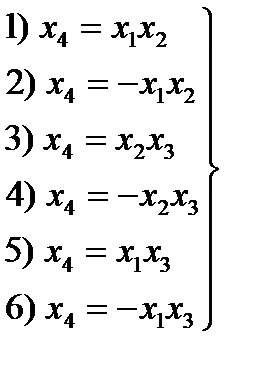 неосновные;
неосновные; 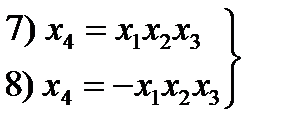 главные.
главные.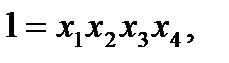
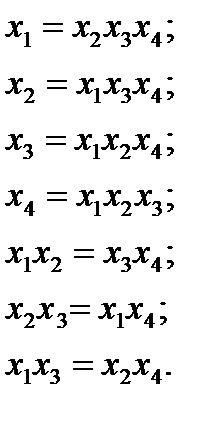
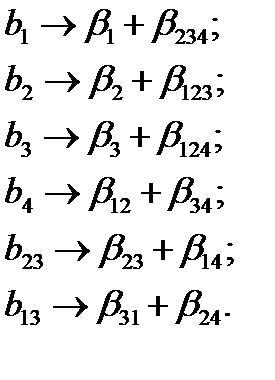
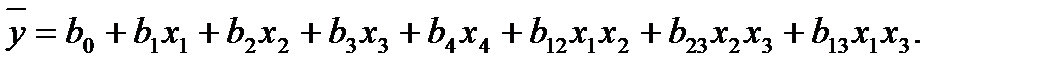
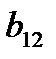 оценивает не только
оценивает не только 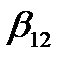 но и
но и 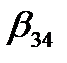 ,
, 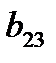 – не только
– не только 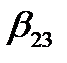 но и
но и 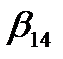 и т. д.
и т. д.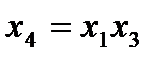 . Получим новый план, у которого
. Получим новый план, у которого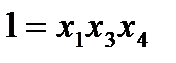 . Система генераторов будет следующей:
. Система генераторов будет следующей: 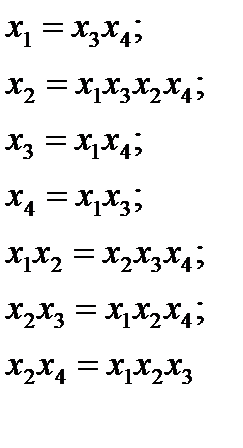 .
.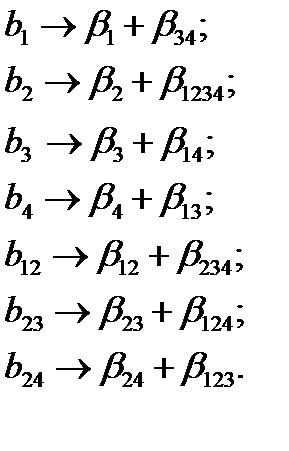
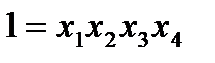 является лучшим. Для него оценки линейных эффектов смешаны лишь с тройными воздей-
является лучшим. Для него оценки линейных эффектов смешаны лишь с тройными воздей-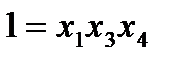 некоторые из этих оценок смеша-
некоторые из этих оценок смеша-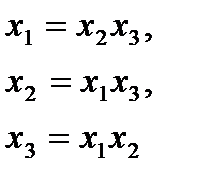
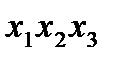 .
.


