
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистический анализ уравнений регрессииСодержание книги
Поиск на нашем сайте
Дисперсия воспроизводимости После постановки опытов и получения уравнения регрессии приступают к его статистическому анализу. При этом решают две задачи: оценивают значимость коэффициентов регрессии и проверяют адекватность математической модели. Соответствующей характеристикой является дисперсия параметра процесса (воспроизводимости), обозначаемая через s 2{ у }. Рассмотрим способы ее вычисления в зависимости от методики дублирования опытов. 1. Равномерное дублирование. Каждый из запланированных опытов повторяется одинаковое число раз, т. е. имеется N серий, в каждой Обозначим результаты опытов первой серии через
где
Аналогично рассчитываются среднее
Отметим, что n – 1 – числа степеней свободы всех дис-
где N(n – 1 ) – число степеней свободы 2. Неравномерное дублирование. Каждый j -й опыт повторяется Числа степеней свободы дисперсий различны:
Число степеней свободы
3. При отсутствии дублированных опытов для оценки дис-
8.2. Оценка точности, значимости коэффициентов регрессии После того как получено уравнение регрессии и рассчитана оценка дисперсии воспроизводимости, следует оценить точность, с которой найдены коэффициенты регрессии. Поскольку они вычисляются по результатам эксперимента, а эти результаты являются случайными величинами, то случайными величинами будут и коэффициенты регрес-сии b Для получения дисперсий коэффициентов регрессии используют матрицу базисных функций Х. Рассмотрим матрицу (Х
Умножив каждый ее элемент на дисперсию воспроизводимости Тогда
По главной диагонали матрицы (5.3) располагаются дисперсии коэффициентов регрессии, а недиагональные элементы – это ковариации между коэффициентами регрессии. Ковариация, так же как и коэффициент корреляции, является мерой линейной статистической связи между
Аналогично коэффициенту корреляции ковариация между не-зависимыми случайными величинами равна нулю. Таким образом, Рассмотрим отдельно случай равномерного дублирования. Для по-лучения оценок дисперсий и ковариаций коэффициентов регрессии следует каждый элемент матрицы Для большинства планов, рекомендуемых теорией эксперимента, существуют простые формулы для отыскания дисперсий коэффициен- При ортогональном планировании отбрасывание незначимых коэф-фициентов регрессии не приводит к изменению оценок остальных коэффициентов. Для ортогональных планов оценки дисперсий без дублирования опытов, т. е. при n = 1
при равномерном дублировании
После того как найдены оценки дисперсий коэффициентов регрессии, следует выявить незначимые коэффициенты, которые в математической модели можно приравнять нулю. Для этого используется t -критерий Стьюдента. Для каждого коэффициента регрессии
В формуле (5.4) в числителе стоит абсолютная величина коэффициента регрессии, в знаменателе – его эмпирический стандарт: корень квадратный из оценки дисперсии. Вычисленную величину Если
При отбрасывании незначимых членов уравнения возникает определенное неудобство, связанное со статистической зависимостью коэффициентов регрессии. Эта зависимость проявляется в том, что С помощью t -критерия можно найти доверительный интервал
Даже простейшая линейная модель позволяет получить важную информацию об объекте исследования. Запишем ее в нормализованных обозначениях факторов: Коэффициенты этой математической модели имеют четкий физический смысл. Очевидно, что коэффициент Чем больше абсолютная величина линейного коэффициента регрессии в модели (5.5), тем сильнее влияние соответствующего фактора. Если, например,
|
||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.007 с.) |

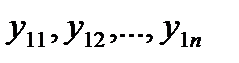 .
. 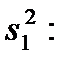
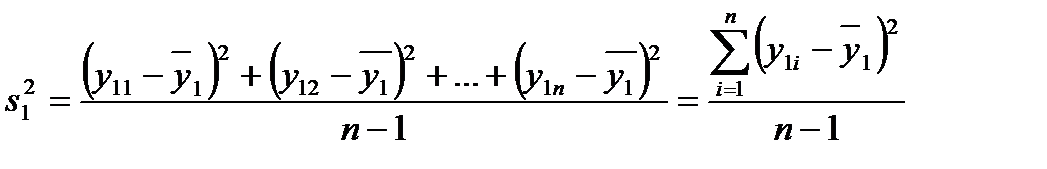 ,
,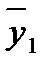 – среднее по серии дублированных опытов;
– среднее по серии дублированных опытов;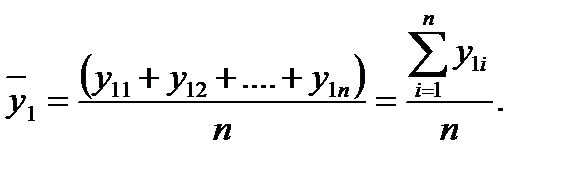
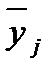 и дисперсии
и дисперсии 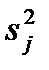 всех остальных опытов:
всех остальных опытов: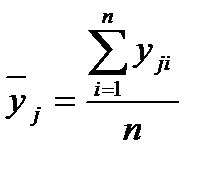 ; (5.1)
; (5.1) 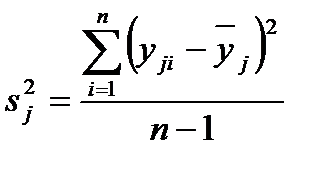 . (5.2)
. (5.2) 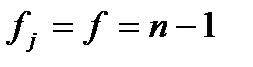 . В качестве дисперсии вос-производимости
. В качестве дисперсии вос-производимости 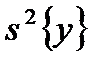 берется среднее арифметическое дисперсий
берется среднее арифметическое дисперсий 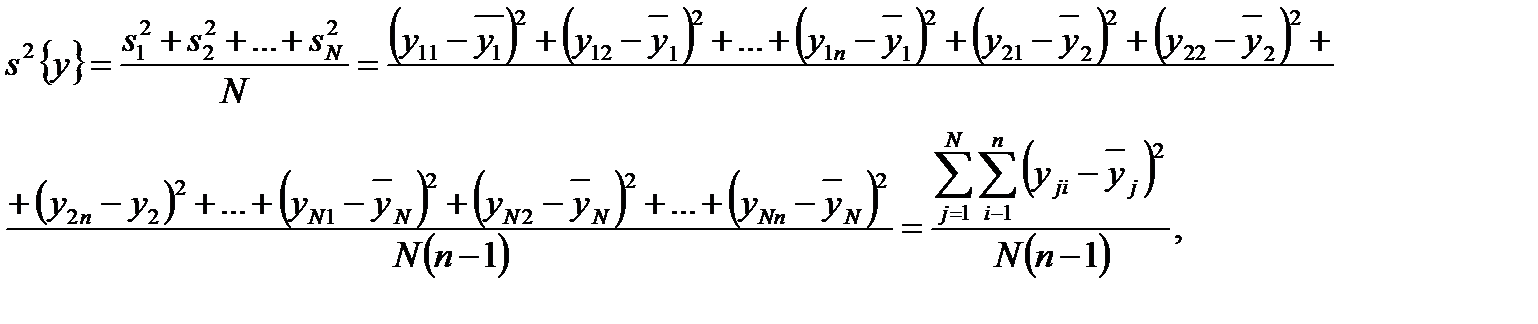
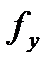 этой дисперсии, равное сумме степеней свободы дисперсий опытов,
этой дисперсии, равное сумме степеней свободы дисперсий опытов, 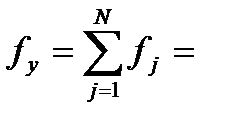 N (n – 1) .
N (n – 1) . 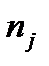 . Как и в предыдущем случае, дисперсии первого, второго,..., j -го опытов
. Как и в предыдущем случае, дисперсии первого, второго,..., j -го опытов 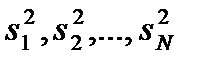 рассчитываются по формулам, аналогичным (5.1, 5.2), только вместо n подставляют
рассчитываются по формулам, аналогичным (5.1, 5.2), только вместо n подставляют 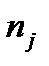 .
. 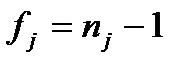 . Диспер-
. Диспер-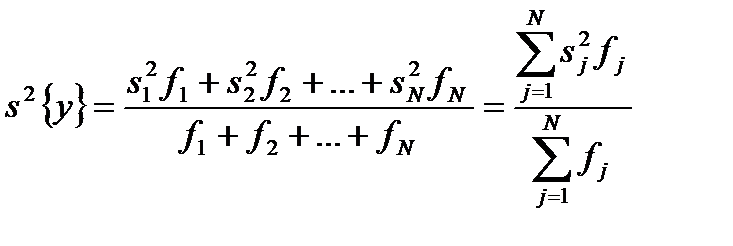 .
.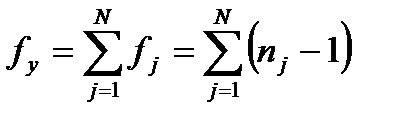 .
.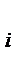 . Поэтому в качестве показателя точности отыскания коэффициен-
. Поэтому в качестве показателя точности отыскания коэффициен-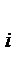 удобно взять его дисперсию
удобно взять его дисперсию 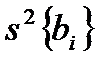 .
.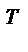 Х)
Х) 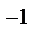 , элементы
, элементы 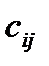 . Это квадратная матрица размером
. Это квадратная матрица размером 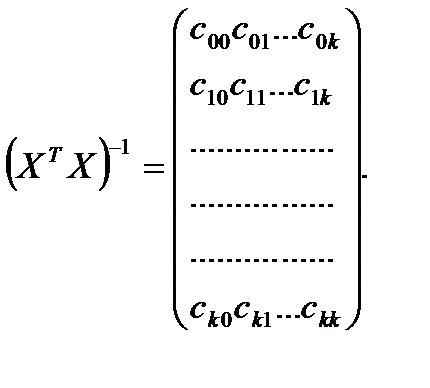
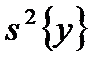 , можно показать, что полученная матрица имеет вид
, можно показать, что полученная матрица имеет вид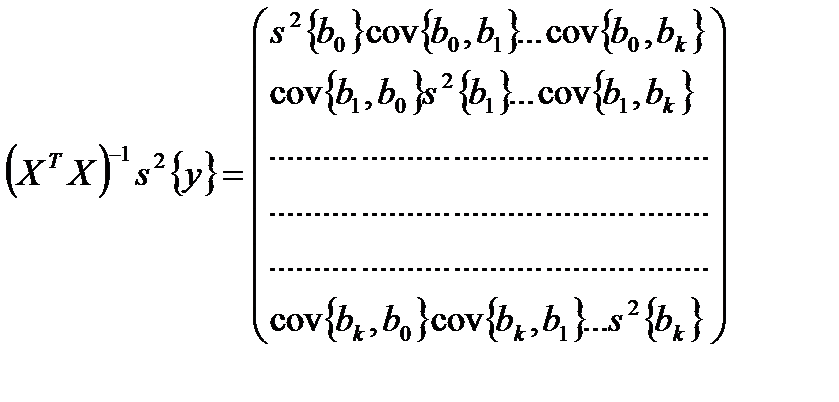 . (5.3.)
. (5.3.)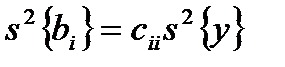 .
.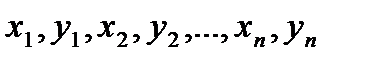 :
: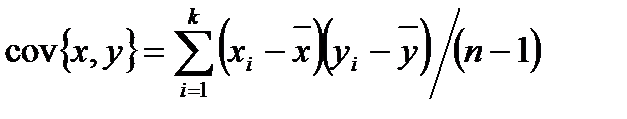 .
.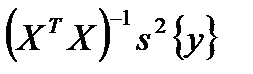 (см. (5.3)) разделить
(см. (5.3)) разделить  , где Р – матрица дубли-рования.
, где Р – матрица дубли-рования.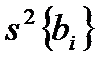 коэффициентов регрессии можно рассчитать по формулам:
коэффициентов регрессии можно рассчитать по формулам: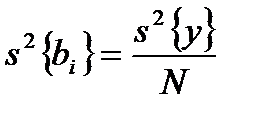 ;
;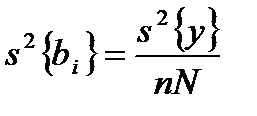 .
.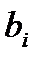 отыскивают t -отно-шение:
отыскивают t -отно-шение: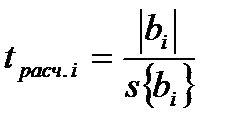 . (5.4)
. (5.4) 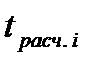 сравнивают с табличным значением
сравнивают с табличным значением 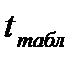 критерия Стьюдента [3]
критерия Стьюдента [3] 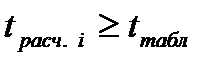 , то коэффициент регрессии значим. Чем
, то коэффициент регрессии значим. Чем  при этом коэффициенте. Если же
при этом коэффициенте. Если же 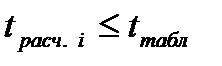 , то коэффициент регрессии
, то коэффициент регрессии 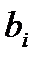 незначим и член в уравнении регрессии должен быть отброшен. С учетом (5.4) условие того, что коэффициент регрессии незначим, можно записать
незначим и член в уравнении регрессии должен быть отброшен. С учетом (5.4) условие того, что коэффициент регрессии незначим, можно записать 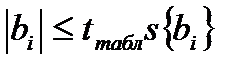 .
. . Обозначим истинную величину этого коэффициента через
. Обозначим истинную величину этого коэффициента через  . Тогда
. Тогда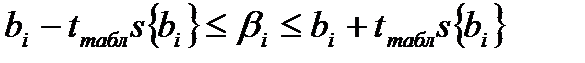 .
.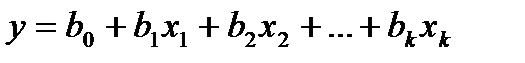 (5.5)
(5.5) 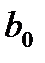 равен значению выходной величины, рассчитанному по уравнению регрессии, если все факторы зафиксированы на основном уровне, т. е. в середине диапазона варьирования. Знак коэффициента
равен значению выходной величины, рассчитанному по уравнению регрессии, если все факторы зафиксированы на основном уровне, т. е. в середине диапазона варьирования. Знак коэффициента 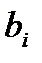 свидетельствует охарактере влияния соответствующего фактора: если
свидетельствует охарактере влияния соответствующего фактора: если 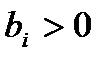 , то с ростом значения фактора
, то с ростом значения фактора 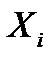 выходная величина растет; если
выходная величина растет; если 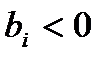 , то с ростом
, то с ростом 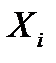 отклик уменьшается. Величина
отклик уменьшается. Величина 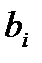 равна приросту выходной величины, полученному при увеличении значения фактора
равна приросту выходной величины, полученному при увеличении значения фактора 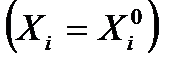 до верхнего уровня
до верхнего уровня 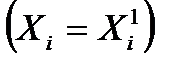 . Как уже указывалось, из вида модели (5.5) следует, что графиком зависимости величины у от любого фактора
. Как уже указывалось, из вида модели (5.5) следует, что графиком зависимости величины у от любого фактора 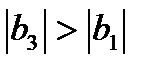 , то можно сделать вывод, что изменение фактора
, то можно сделать вывод, что изменение фактора 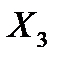 в пределах его диапазона варьирования оказывает большее влияние на изменение отклика, чем варьирование фактора
в пределах его диапазона варьирования оказывает большее влияние на изменение отклика, чем варьирование фактора 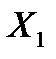 в его диапазоне. Таким образом, с помощью линейной регрессионной модели можно сравнить степень влияния факторов на выходную величину
в его диапазоне. Таким образом, с помощью линейной регрессионной модели можно сравнить степень влияния факторов на выходную величину 


