Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки результатов наблюденийСодержание книги
Поиск на нашем сайте Множество значений случайной величины, полученных в результате эксперимента или наблюдений над объектом исследования, представляет собой статистическую совокупность. Статистическая совокупность, содержащая в себе все возможные значения случайной величины, называется генеральной статистической совокупностью. Совокупность, включающая некоторую часть элементов генеральной совокупности, называется выборочной статистической совокупностью. По результатам экспериментов практически всегда сталкиваются именно с выборочной статистической совокупностью. В дальнейшем будем называть ее выборкой, а число опытов (наблюдений) п, содержащееся в выборке, – объемом. При повторении опытов в одинаковых условиях обычно обнаруживается закономерность в частоте появления тех или иных результатов. Некоторые значения случайной величины появляются значительно чаще других, при этом они группируются относительно некоторого значения – центра Му. Для описания этого явления используется вероятностный подход. Пусть р Величину Му называют математическим ожиданием или генеральным средним случайной величины. Однако только математическое ожидание не может отобразить все характерные черты статистической совокупности. Исследователю, кроме того, необходимо знать изменчивость (вариацию) наблюдаемой характеристики объекта. Рассеивание случайной величины относительно математического ожидания характеризуется величиной, называемой дисперсией. Обычно она обозначается через Дисперсию Формулы (2.1) и (2.2) справедливы для дискретных случайных величин. Для непрерывных случайных величин математическое ожидание и дисперсия выражаются через соответствующие интегралы. Поскольку экспериментатор имеет дело не с генеральной совокупностью, а с выборкой, необходимы формулы, позволяющие приближенно оценить математическое ожидание Му и дисперсию Найденное значение Числитель данной формулы представляет собой сумму квадратов отклонений значений случайной величины от среднего значения Формулу (2.4) можно преобразовать к виду, более удобному для вычислений: Величина является оценкой среднего квадратичного отклонения о выборки. Ее также называют выборочным стандартом. Часто для оценки изменчивости (вариации) случайных величин используют коэффициент вариации v (%): Коэффициент вариации характеризует не абсолютное, а относитель-ное рассеивание случайной величины относительно среднего. Важное значение в статистике имеют также следующие статисти-ческие показатели: средняя квадратичная ошибка среднего значения показатель точности среднего значения, %: ошибка среднего квадратичного отклонения Статистическая совокупность может иногда содержать сотни и даже тысячи наблюдений. При этом анализ экспериментального материала, Для вычисления выборочного среднего k = 1 + 3,21 g (n), (2.11) где n – объем выборки. Значение k, найденное по этой формуле, округляется до ближайшего целого. Чаще всего используются интервалы равной длины. В этом случае длина (h) каждого интервала
Далее определяются границы интервалов. Так, первый интервал лежит в пределах
где i = 1, 2,… k. Затем подсчитывается число наблюдений, попавших в каждый интервал. Обозначим его через m Предварительно договариваются, к какому интервалу приписывать значение случайной величины, попавшее на границу интервала.
Тогда выборочное среднее При использовании формул (2.12) и (2.13) для получения оценок математического ожидания и дисперсии можно и не определять числовых значений элементов выборки. Достаточно знать, в какой интервал попадет каждое значение случайной величины. Данные записывают в виде статистического ряда (табл. 2.1).
Таблица 2.1. Статистический ряд
График, построенный по данным статистического ряда, называют гистограммой. При построении гистограммы по оси абсцисс отклады- Пусть, например, в результате измерения шероховатости поверхно-сти деталей получено n = 140 значений высот неровностей разруше-
Таблица 2.2 Высоты неровностей разрушения
Из табл. 2.2 видно, что высота микронеровностей у изменяется
Таблица 2.3 Статистические интервалы
Изображенная на рис. 2.1 гистограмма соответствует статистическому ряду, приведенному в табл. 2.3. Поскольку сумма всех относительных частот составляет единицу, то площадь гистограммы также равна единице. С увеличением числа опытов Если одновременно с увеличением числа опытов n увеличивать Для случайных величин, имеющих разную природу, статистические распределения могут быть различными. Известны, например, распре-деления Пуассона, Пирсона, биноминальное и многие другие. Среди них существует распределение, называемое нормальным (или гауссовским), которое применяется наиболее часто и играет важную роль в теории вероятностей и математической статистике.
Рис. 2.1. Гистограмма распределения Рис. 2.2. Кривая плотности нормальногораспределения
Далее будем исходить из предположения, что результаты наблюдений свободны от систематических ошибок, а случайные ошибки (а значит,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

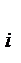 – вероятность того, что случайная величина, являющаяся результатом эксперимента, примет значение у
– вероятность того, что случайная величина, являющаяся результатом эксперимента, примет значение у 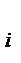 из генеральной совокупности, то величину Му можно найти
из генеральной совокупности, то величину Му можно найти 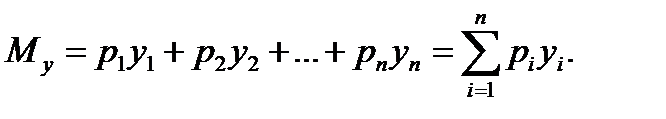 (2.1)
(2.1)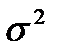 . Для генеральной совокупности дисперсия определяется по формуле
. Для генеральной совокупности дисперсия определяется по формуле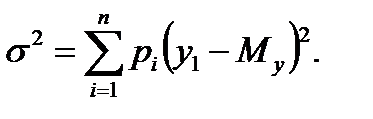 (2.2)
(2.2)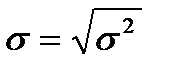 . Как и дисперсия, среднее квадратическое отклонение является характеристикой рассеивания значений случайной величины относительно математического ожидания.
. Как и дисперсия, среднее квадратическое отклонение является характеристикой рассеивания значений случайной величины относительно математического ожидания.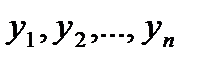 . Наилучшей оценкой для математи-ческого ожидания Му является среднее арифметическое («среднее»)
. Наилучшей оценкой для математи-ческого ожидания Му является среднее арифметическое («среднее»)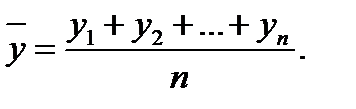 (2.3)
(2.3)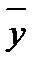 называют также выборочным средним в отличие от генерального среднего Му. Оценкой дисперсии
называют также выборочным средним в отличие от генерального среднего Му. Оценкой дисперсии 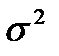 случайной величины является выборочная или эмпирическая дисперсия
случайной величины является выборочная или эмпирическая дисперсия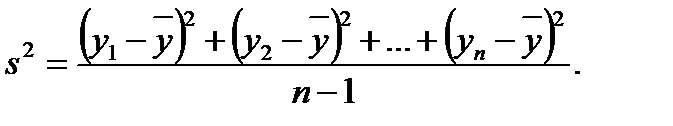 (2.4)
(2.4) ,
, 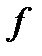 :
: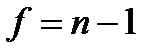 (2.5)
(2.5)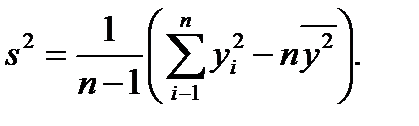 (2.6)
(2.6)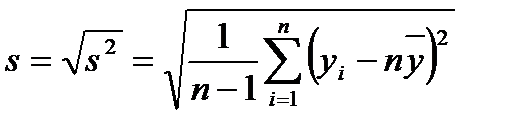 (2.7)
(2.7)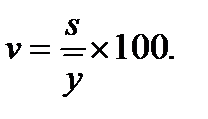 (2.8)
(2.8)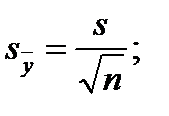 (2.9)
(2.9)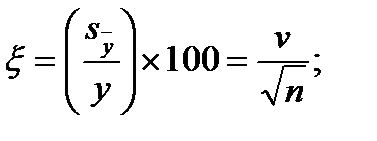 (2.10)
(2.10)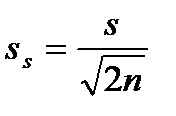 .
.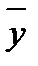 и выборочной дисперсии
и выборочной дисперсии 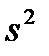 в подобных случаях прибегают к группированию данных. При этом
в подобных случаях прибегают к группированию данных. При этом 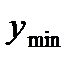 до
до 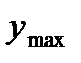 разбивается
разбивается 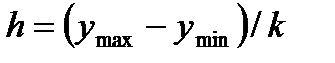 .
.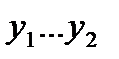 , где
, где 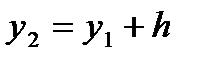 ; второй интервал – в пределах
; второй интервал – в пределах 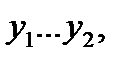 где
где 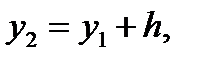 и т. д. Для каждого i- гоинтервала вычисляется его середина
и т. д. Для каждого i- гоинтервала вычисляется его середина 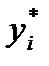 по формуле
по формуле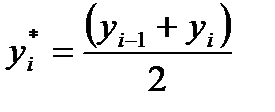 ,
,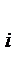 , i = 1, 2,…, k.
, i = 1, 2,…, k.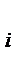 , всегда относится к i + 1-му интервалу. Сумма
, всегда относится к i + 1-му интервалу. Сумма 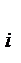 равна объему выборки:
равна объему выборки: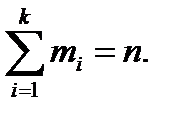
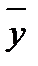 и выборочная дисперсия
и выборочная дисперсия 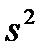 определяются соответственно по формулам:
определяются соответственно по формулам: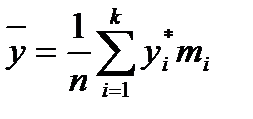 (2.12)
(2.12)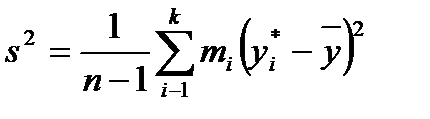 (2.13)
(2.13)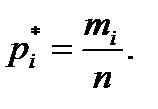 .
.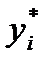
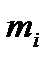
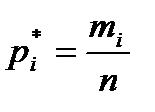
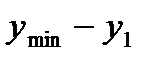
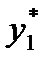
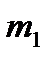
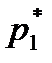
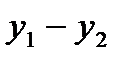
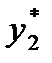
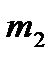
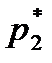
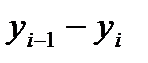
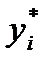
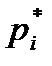
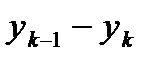
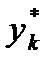
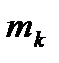
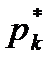
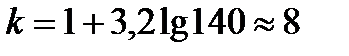 . Результаты подсчета значений
. Результаты подсчета значений 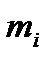 и относительных частот
и относительных частот 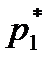 приведены в четвертом
приведены в четвертом 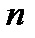 значение каждой частоты становится все ближе к соответствующей вероятности
значение каждой частоты становится все ближе к соответствующей вероятности 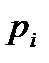 . Это утверждение, выражающее требование статистической устойчивости частот, является важнейшей предпосылкой применения статистических методов.
. Это утверждение, выражающее требование статистической устойчивости частот, является важнейшей предпосылкой применения статистических методов.