
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка нормальности распределенияСодержание книги
Поиск на нашем сайте
При рассмотрении всех предыдущих статистических процедур исходили из того, что выходная величина подчиняется нормальному закону распре-деления. Это предположение можно проверить разными способами. Наиболее точным из них является применение критерия где
значения которой для Ф(–z) = –Ф(z). Следующим этапом является вычисление величины По выбранному уровню значимости q и числу степеней свободы Менее употребительной является проверка нормальности распре-деления по критерию Приближенная проверка нормальности распределения может быть проведена с помощью показателей асимметрии и эксцесса. Выборочные показатели асимметрии А и эксцесса Е рассчитывают по формулам:
где п – объем выборки, s – ее эмпирический стандарт. Далее вычисляют средние квадратические отклонения для асим-метрии
Если хотя бы одна из характеристик А или Е по абсолютной величине существенно (в 2–3 раза) превосходит соответствующее среднее квадратическое отклонение, то следует усомниться в нормальности распределения и провести более тщательную проверку с помощью критерия Пирсона или Колмогорова. В противном случае гипотеза
Коэффициент корреляции Во многих случаях целью экспериментальных исследований является установление и изучение зависимости между некоторыми величинами. Если каждая из них является случайной, то используют методы корреляционного анализа. Так, методами корреляционного анализа можно оценить степень взаимосвязи между пределом прочности материала Между двумя случайными величинами имеется статистическая связь, если при изменении одной из них меняется распределение другой. Для оценки статистической связи по данным эксперимента широко использу-ется выборочный коэффициент корреляции. Пусть проведено п наблюде-ний и в каждом из них определились значения параметров (признаков) х
По каждой из них найдем среднее арифметическое которую можно переписать в виде, более удобном для вычислений: При расчетах полезно иметь в виду, что выборочный коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения х и y. Коэффициент корреляции всегда лежит в пределах –1
и сравнивают ее с табличным значением t -критерия Стьюдента, найден-ным при выбранном уровне значимости q и числе степеней свободы
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА Основные сведения Планирование эксперимента – это постановка опытов по некоторой заранее составленной схеме, обладающей некоторыми оптимальными свойствами. При этом необходимо: стремиться к минимизации числа опытов; одновременно варьировать все факторы, определяющие протекание процесса по специальным алгоритмам (правилам); использовать математический аппарат, формализующий ряд действий экспериментатора; иметь четкую стратегию, позволяющей принимать обоснованные решения после каждой проведенной серии опытов. Таким образом, планирование эксперимента – это комплекс приемов, позволяющих исследователю оптимально поставить эксперимент, со-образуясь с целью исследования (со стремлением получить максимум информации) при необходимости экономить средства (число опытов), Планирование эксперимента базируется на кибернетическом подходе к объекту исследований. Для описания объекта исследований модели-рования используется неизвестная система (рис. 3.1), подверженная различным воздействиям.
Рис. 3.1. Схема описания объекта моделирования
Используя планирование эксперимента, исследователь априори (до постановки опыта) может назвать виды входных и выходных внешних воздействий, связанных с объектом исследований, но содержание «черного ящика» пока остается нераскрытым. При рассмотрении «черного ящика» различают два основных вида параметров: входные управляемые Выходные параметры часто называют параметрами оптимизации, целевыми функциями, выходными величинами и т. д.
6.2. Назначение планирования эксперимента
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.153 (0.009 с.) |

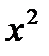 Пирсона, для чего необ-ходима выборка достаточно большого объема:
Пирсона, для чего необ-ходима выборка достаточно большого объема: 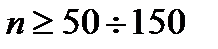 . Диапазон измене-ния выходной величины в выборке разбивается на l интервалов так, чтобы эти интервалы покрывали всю ось от –∞ до +∞ и в каждый интервал попадало не менее пяти значений выходной величины. Подсчитывают количество т наблюдений, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый i -й интервал:
. Диапазон измене-ния выходной величины в выборке разбивается на l интервалов так, чтобы эти интервалы покрывали всю ось от –∞ до +∞ и в каждый интервал попадало не менее пяти значений выходной величины. Подсчитывают количество т наблюдений, попавших в каждый интервал. Затем вычисляют теоретические вероятности попадания случайной величины в каждый i -й интервал:
 (2.24)
(2.24) – среднее арифметическое выборки; s – среднее квадратическое отклонение выборки;
– среднее арифметическое выборки; s – среднее квадратическое отклонение выборки; 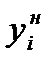 – нижняя граница i -го интервала;
– нижняя граница i -го интервала;  – верхняя граница i -го интервала; Ф
– верхняя граница i -го интервала; Ф  – нормированная функция Лапласа:
– нормированная функция Лапласа: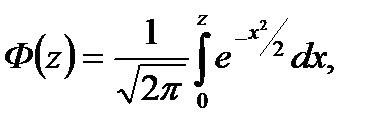
 и
и 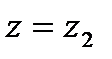 определяют из специальных таблиц. При отыскании значений этой функции для отрицательных значений аргумента следует иметь в виду, что функция Ф(z) нечетная:
определяют из специальных таблиц. При отыскании значений этой функции для отрицательных значений аргумента следует иметь в виду, что функция Ф(z) нечетная: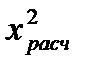 по формуле
по формуле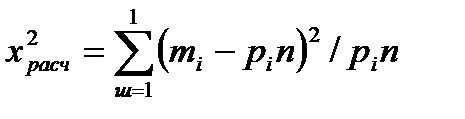 (2.25)
(2.25)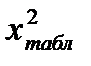 . Гипотезу о нормальности распределения можно принять, если
. Гипотезу о нормальности распределения можно принять, если 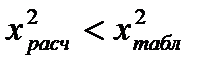 .
.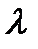 Колмогорова.
Колмогорова.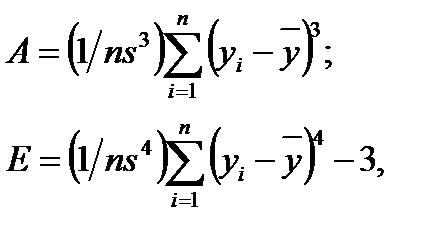
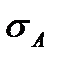 и эксцесса
и эксцесса 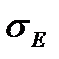 :
: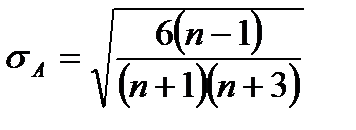 ;
;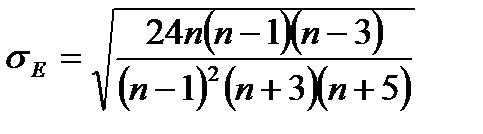 .
.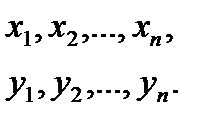
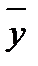 и
и 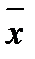 , а также выборочный стандарт
, а также выборочный стандарт 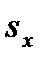 и
и 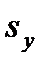 . Выборочный коэффициент корреляции r рассчитывается по формуле
. Выборочный коэффициент корреляции r рассчитывается по формуле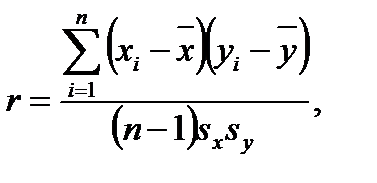 (2.26)
(2.26)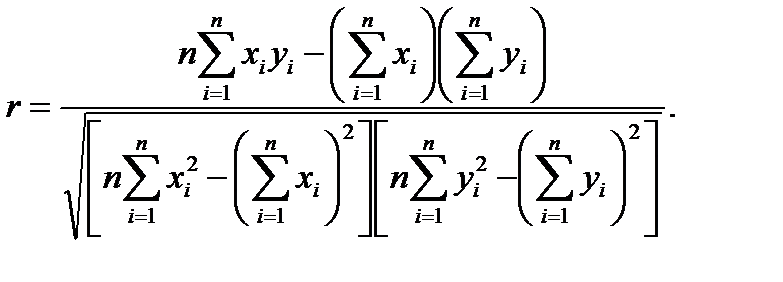 (2.27)
(2.27)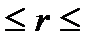 1
1 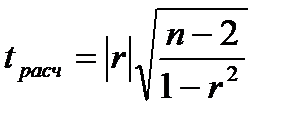 (2.28)
(2.28)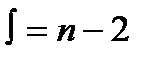 . Если
. Если 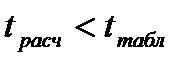 принимается гипотеза о некоррелированности величин х и у. В противном случае коэффициент корреляции значимо отличается от нуля, т. е. между величинами х и у существует линейная статистическая связь.
принимается гипотеза о некоррелированности величин х и у. В противном случае коэффициент корреляции значимо отличается от нуля, т. е. между величинами х и у существует линейная статистическая связь.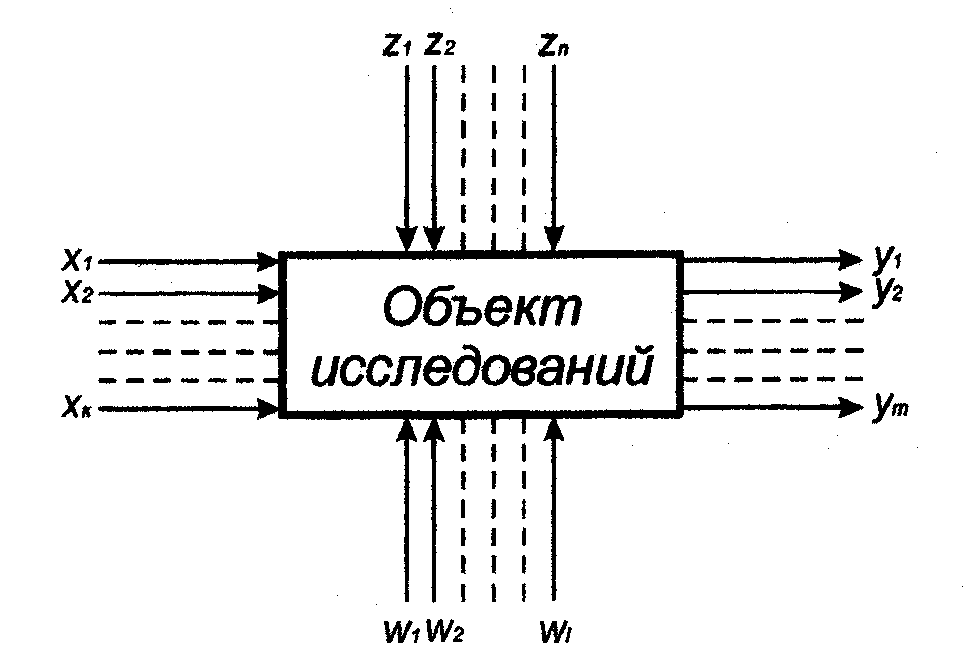
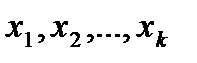 ) и выходные (
) и выходные (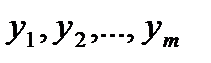 ). Некоторые из них могут быть приняты в качестве критериев оптимизации. Кроме того, на объект воздействуют неуправляемые параметры. Одни из них (
). Некоторые из них могут быть приняты в качестве критериев оптимизации. Кроме того, на объект воздействуют неуправляемые параметры. Одни из них (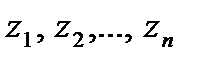 ) могут контролироваться в процессе постановки опытов без их целе-направленного изменения, другие (
) могут контролироваться в процессе постановки опытов без их целе-направленного изменения, другие (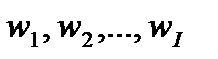 ) являются неконтроли-руемыми (из-за недостатка информации) и относятся к возмущающим воздействиям.
) являются неконтроли-руемыми (из-за недостатка информации) и относятся к возмущающим воздействиям.


