

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Обработка результатов косвенных измерений
Похожие статьи вашей тематики
Косвенное измерение – определение искомого значения величины на основании результатов прямых измерений других величин, функционально связанных с искомой величиной.
Рекомендации по обработке результатов косвенных измерений
Всю обработку результатов косвенных измерений следует проводить в следующем порядке.
1. Записать выражение, описывающее функциональную связь искомой физической величины y с физическими величинами x 1, x 2, x 3… xm, подвергаемым прямым измерениям:
y = f (x 1, x 2, x 3… xm). (2.1).
2. Определить в соответствии с рекомендациями 1.1:
‹ x 1›± Δ x 1; ‹ x 2›± Δ x 2; ‹ x 3›± Δ x 3; …‹ xm ›± Δ xm ..
3. Вычислить ‹ y › подстановкой ‹ x 1›, ‹ x 2›, ‹ x 3›…‹ xm › в f (x 1, x 2, x 3,… xm).
4. Определить частные производные:
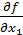 , , 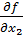 , ,  , … , … 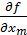
5. Вычислить значения частных производных 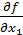 , , 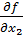 , ,  , … , … 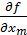 для x 1 = ‹ x 1 ›, x 2 = ‹ x 2 ›, x 3 = ‹ x 3 ›,... xm = ‹ xm ›. для x 1 = ‹ x 1 ›, x 2 = ‹ x 2 ›, x 3 = ‹ x 3 ›,... xm = ‹ xm ›.
6. Вычислить полную погрешность Δ y искомой физической величины y с помощью выражения:
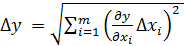 . (2.2) . (2.2)
Следует отметить, что, если в выражении (2.1) всего одна независимая переменная x, то выражение (2.2) преобразуется к виду:
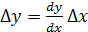 . (2.3) . (2.3)
7. Округлить результаты.
8. Вычислить относительную погрешность результата измерения (при необходимости).
9. Записать результат измерения в виде:
y = ‹ y ›± Δ y для P = …
δ =…
Далее для успешного закрепления изложенного материала рассмотрим пример обработки результатов косвенных измерений.
Пример обработки результатов косвенных измерений
Определить сопротивление R электрической цепи постоянного тока по результатам измерения напряжения U и тока I:
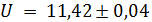 [В]; [В]; 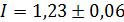 [мA] для Р = 0,95. [мA] для Р = 0,95.
1. В соответствии с законом Ома:
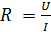 . .
2. Вычисляем значение 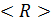 : :
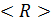 = = 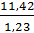 = 9,285 [кОм]. = 9,285 [кОм].
3. Определяем частные производные:
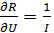 ; ; 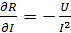 . .
4. Рассчитываем значения частных производных для соответствующих значений 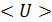 ( 11,42 В) и ( 11,42 В) и 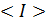 (1,23 мА): (1,23 мА):
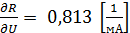 , , 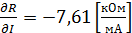 . .
5. Используя выражение (2.2), определяем абсолютную погрешность Δ R измерения искомого сопротивления:
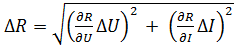 = = 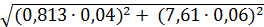 = 0,458 [кОм]. = 0,458 [кОм].
6. Рассчитываем относительную погрешность: 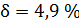 . .
7. Результат измерения (с округлением до 2-го знака после запятой):
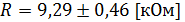 для Р = 0,95; для Р = 0,95;
δ = 4,9 %.
Задания по обработке результатов косвенных измерений
Обработать результаты и записать конечный результат измерения.
Задание 2.3.1.
Требуется определить монохроматическую оптическую плотность D оптических элементов на длине волны λ = 632 нм для доверительной вероятности P = 0,95. Оптическая плотность величина безразмерная и связана с коэффициентом пропускания τ зависимостью:
D = lg(1/τ)
В таблице 2.1 приведены результаты многократных измерений коэффициентов пропускания оптических элементов.
Таблица 2.1 – Результаты многократных измерений коэффициентов пропускания оптических элементов
| № светофильтра
| i
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| | 1
|
τ
| 0,115
| 0,112
| 0,110
| 0,113
| 0,116
| 0,101
| 0,117
| 0,115
| | 2
| 0,121
| 0,119
| 0,117
| 0,122
| 0,129
| 0,120
| 0,118
| 0,117
| | 3
| 0,0998
| 0,0997
| 0,0999
| 0,0999
| 0,0997
| 0,1210
| 0,0996
| 0,0996
| | 4
| 0,0875
| 0,0879
| 0,0881
| 0,0801
| 0,0883
| 0,0879
| 0,0880
| 0,0878
| | 5
| 0,0795
| 0,0799
| 0,0801
| 0,0792
| 0,0780
| 0,0797
| 0,0793
| 0,0798
| | 6
| 0,103
| 0,117
| 0,115
| 0,115
| 0,112
| 0,110
| 0,113
| 0,116
| | 7
| 0,117
| 0,122
| 0,132
| 0,120
| 0,118
| 0,117
| 0,121
| 0,119
| | 8
| 0,0999
| 0,0997
| 0,1110
| 0,0996
| 0,0996
| 0,0998
| 0,0997
| 0,0999
| | 9
| 0,0875
| 0,0883
| 0,0879
| 0,0880
| 0,0878
| 0,0879
| 0,0881
| 0,0809
| | 10
| 0,0797
| 0,0793
| 0,0798
| 0,0795
| 0,0799
| 0,0801
| 0,0792
| 0,0775
| | 11
| 0,0654
| 0,0651
| 0,0601
| 0,0657
| 0,0650
| 0,0659
| 0,0661
| 0,0658
| | 12
| 0,0561
| 0,0560
| 0,0569
| 0,0571
| 0,0589
| 0,0562
| 0,0564
| 0,0566
| | 13
| 0,0501
| 0,0507
| 0,0502
| 0,0505
| 0,0584
| 0,0507
| 0,0505
| 0,0509
| | 14
| 0,0499
| 0,0497
| 0,0441
| 0,0496
| 0,0498
| 0,0497
| 0,0494
| 0,0496
| | 15
| 0,0456
| 0,0404
| 0,0450
| 0,0457
| 0,0455
| 0,0452
| 0,0451
| 0,0455
| | 16
| 0,0650
| 0,0659
| 0,0661
| 0,0658
| 0,0654
| 0,0651
| 0,0621
| 0,0657
| | 17
| 0,0562
| 0,0564
| 0,0566
| 0,0561
| 0,0560
| 0,0569
| 0,0571
| 0,0599
| | 18
| 0,0507
| 0,0505
| 0,0509
| 0,0501
| 0,0507
| 0,0502
| 0,0505
| 0,0554
| | 19
| 0,0496
| 0,0498
| 0,0497
| 0,0494
| 0,0496
| 0,0499
| 0,0497
| 0,0451
| | 20
| 0,0457
| 0,0455
| 0,0452
| 0,0451
| 0,0455
| 0,0456
| 0,0424
| 0,0450
| | 21
| 0,0115
| 0,0112
| 0,0110
| 0,1113
| 0,0116
| 0,0101
| 0,0117
| 0,0115
| | 22
| 0,0121
| 0,0119
| 0,0117
| 0,122
| 0,0129
| 0,0120
| 0,0118
| 0,0117
| | 23
| 0,0099
| 0,0099
| 0,0099
| 0,0099
| 0,0009
| 0,0121
| 0,0099
| 0,0099
| | 24
| 0,0087
| 0,0087
| 0,0088
| 0,1804
| 0,0088
| 0,0087
| 0,0088
| 0,0087
| | 25
| 0,0103
| 0,0117
| 0,0115
| 0,0115
| 0,1128
| 0,0110
| 0,0113
| 0,0116
| | 26
| 0,0117
| 0,0122
| 0,0132
| 0,0220
| 0,0118
| 0,0117
| 0,0121
| 0,0119
| | 27
| 0,1999
| 0,1997
| 0,1110
| 0,1996
| 0,1996
| 0,1998
| 0,1997
| 0,1999
| | 28
| 0,2875
| 0,2883
| 0,2879
| 0,2880
| 0,2878
| 0,2879
| 0,1881
| 0,2809
| | 29
| 0,1654
| 0,1651
| 0,601
| 0,1657
| 0,1065
| 0,1659
| 0,1661
| 0,1658
| | 30
| 0,2561
| 0,2560
| 0,2569
| 0,2571
| 0,2589
| 0,1562
| 0,2564
| 0,2566
| | 31
| 0,2654
| 0,2651
| 0,2601
| 0,2657
| 0,2650
| 0,2659
| 0,2661
| 0,2658
| | 32
| 0,3561
| 0,3560
| 0,3569
| 0,3571
| 0,3589
| 0,3562
| 0,3564
| 0,3566
| | 33
| 0,2501
| 0,2507
| 0,2502
| 0,2505
| 0,2584
| 0,2507
| 0,2505
| 0,2509
| | 34
| 0,2499
| 0,2497
| 0,2441
| 020496
| 0,2498
| 0,2497
| 0,2494
| 0,2496
| | 35
| 0,3456
| 0,3404
| 0,3450
| 0,3457
| 0,3455
| 0,3452
| 0,3451
| 0,3455
| | 36
| 0,3650
| 0,3659
| 0,3661
| 0,3658
| 0,3654
| 0,3651
| 0,3621
| 0,3657
| | 37
| 0,4562
| 0,4564
| 0,4566
| 0,4561
| 0,4560
| 0,4569
| 0,4571
| 0,4599
| | 38
| 0,4507
| 0,4505
| 0,4509
| 0,4501
| 0,4507
| 0,4502
| 0,4505
| 0,4554
| | 39
| 0,4496
| 0,4498
| 0,4497
| 0,4494
| 0,4496
| 0,4499
| 0,4497
| 0,4451
| | 40
| 0,5457
| 0,5455
| 0,5452
| 0,5451
| 0,5455
| 0,5456
| 0,5424
| 0,5450
|
Задание 2.3.2
Определить площадь S детали в виде диска по многократным результатам измерения его диаметра D (таблица 2.2). Доверительная вероятность P = 0,99. Измерения проводились с помощью штангенциркуля.
Характеристики штангенциркуля:
предел допускаемой погрешности 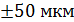 . .
Результаты измерения в таблице 2.2 относятся к нормальному распределению.
Таблица 2.2 – Результаты многократных измерений диаметра диска
| № диска
| i
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| | 1
|
D, мм
| 25,41
| 25,39
| 25,35
| 25,27
| 25,99
| 25,38
| 25,41
| 25,40
| 25,36
| | 2
| 27,25
| 27,22,
| 27,35
| 27,22
| 27,26
| 27,00
| 27,23
| 27,24
| 27,26,
| | 3
| 28,98
| 28,51
| 28,49
| 28,47
| 28,49
| 28,51
| 28,52
| 28,50
| 28,52
| | 4
| 29,19
| 19,21
| 29,20
| 29,23
| 29,18
| 29,17
| 29,44
| 29,25
| 29,19
| | 5
| 29,51
| 29,41
| 29,50
| 29,47
| 30,01
| 29,52
| 29,53
| 29,50
| 29,47
| | 6
| 25,79
| 25,38
| 25,41
| 25,40
| 25,36
| 25,37
| 25,41
| 25,39
| 25,35
| | 7
| 27,05
| 27,23
| 27,24
| 27,26,
| 27,23
| 27,00
| 27,22,
| 27,35
| 27,22
| | 8
| 28,47
| 28,49
| 28,51
| 28,52
| 28,50
| 28,52
| 28,48
| 28,91
| 28,51
| | 9
| 29,18
| 29,17
| 29,49
| 29,25
| 29,19
| 29,18
| 29,19
| 19,21
| 29,20
| | 10
| 30,00
| 29,52
| 29,53
| 29,50
| 29,47
| 29,48
| 29,51
| 29,41
| 29,50
| | 11
| 45,41
| 45,44
| 45,23
| 45,40
| 45,39
| 45,42
| 45,44
| 45,38
| 45,39
| | 12
| 45,21
| 45,22
| 45,20
| 45,19
| 45,02
| 45,24
| 45,18
| 45,17
| 45,20
| | 13
| 45,61
| 45,60
| 45,78
| 45,59
| 45,57
| 45,56
| 45,59
| 45,61
| 45,62
| | 14
| 42,42
| 42,21
| 42,41
| 42,44
| 42,40
| 42,45
| 42,38
| 42,39
| 42,37
| | 15
| 43,51
| 43,50
| 43,55
| 43,44
| 43,39
| 43,49
| 43,48
| 43,49
| 43,52
| | 16
| 45,39
| 45,42
| 45,44
| 45,38
| 45,39
| 45,40
| 45,41
| 45,44
| 45,20
| | 17
| 45,19
| 45,05
| 45,24
| 45,18
| 45,17
| 45,20
| 45,22
| 45,21
| 45,22
| | 18
| 45,56
| 45,59
| 45,61
| 45,62
| 45,60
| 45,61
| 45,60
| 45,73
| 45,59
| | 19
| 42,38
| 42,39
| 42,37
| 42,38
| 42,42
| 42,24
| 42,41
| 42,44
| 42,40
| | 20
| 43,29
| 43,49
| 43,48
| 43,49
| 43,52
| 43,50
| 43,51
| 43,50
| 43,55
| | 21
| 125,41
| 125,39
| 125,35
| 125,27
| 125,99
| 125,38
| 125,41
| 125,40
| 125,36
| | 22
| 127,25
| 127,22
| 127,35
| 127,22
| 127,26
| 127,00
| 127,23
| 127,24
| 127,26
| | 23
| 128,98
| 128,51
| 128,49
| 128,47
| 128,49
| 128,51
| 128,52
| 128,50
| 128,52
| | 24
| 129,19
| 119,21
| 129,20
| 129,23
| 129,18
| 129,17
| 129,44
| 129,25
| 129,19
| | 25
| 129,51
| 129,41
| 129,50
| 129,47
| 130,01
| 129,52
| 129,53
| 129,50
| 129,47
| | 26
| 130,00
| 129,52
| 129,53
| 129,50
| 129,47
| 129,48
| 129,51
| 129,41
| 129,50
| | 27
| 145,41
| 145,44
| 145,23
| 145,40
| 145,39
| 145,42
| 145,44
| 145,38
| 145,39
| | 28
| 145,61
| 145,60
| 145,78
| 145,59
| 145,57
| 145,56
| 145,59
| 145,61
| 145,62
| | 29
| 5,21
| 5,22
| 5,20
| 5,19
| 5,02
| 5,24
| 5,18
| 5,17
| 5,20
| | 30
| 143,29
| 143,49
| 143,48
| 143,49
| 143,52
| 143,50
| 143,51
| 143,50
| 143,55
| | 31
| 245,61
| 245,60
| 245,78
| 245,59
| 245,57
| 245,56
| 245,59
| 245,61
| 245,62
| | 32
| 225,41
| 225,39
| 225,35
| 225,27
| 225,99
| 225,38
| 225,41
| 225,40
| 225,36
| | 33
| 227,25
| 227,22
| 227,35
| 27,22
| 227,26
| 227,00
| 227,23
| 227,24
| 227,26
| | 34
| 228,98
| 228,51
| 228,49
| 228,47
| 228,49
| 228,51
| 228,52
| 228,50
| 228,52
| | 35
| 229,19
| 219,21
| 229,20
| 229,23
| 229,18
| 229,17
| 229,44
| 229,25
| 229,19
| | 36
| 229,51
| 229,41
| 229,50
| 229,47
| 230,01
| 229,52
| 229,53
| 229,50
| 229,47
| | 37
| 230,00
| 229,52
| 229,53
| 229,50
| 229,47
| 229,48
| 229,51
| 229,41
| 229,50
| | 38
| 245,41
| 245,44
| 245,23
| 245,40
| 245,39
| 245,42
| 245,44
| 245,38
| 245,39
| | 39
| 345,61
| 345,60
| 345,78
| 345,59
| 345,57
| 345,56
| 345,59
| 345,61
| 345,62
| | 40
| 328,47
| 328,49
| 328,51
| 328,52
| 328,50
| 328,52
| 328,48
| 328,91
| 328,51
|
Задание 2.3.3
При продаже золотого песка старателем скупщику на Аляске проводилось взвешивание с помощью аптекарских весов. По требованию старателя взвешивание песка осуществлялось многократно с поочередным перемещением песка с одной чашки весов на другую. В таблице 2.3 представлены результаты многократных взвешиваний золотого песка. На рис. 2.1, а,б показаны условия взвешивания (баланса) для первого и второго случаев.
L 1, L 2 – длины плеч коромысла весов Определить массу (mx) золотого песка для доверительной вероятности Р = 0,95.
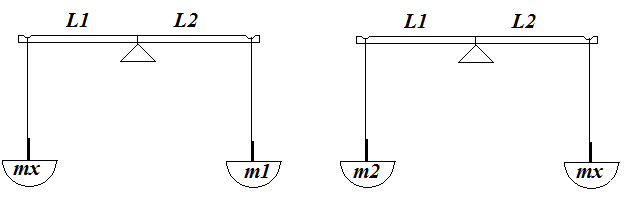
Рис. 2.1 – Этапы взвешивания золотого песка
а) песок на левой чашке; б) песок на правой чашке
Таблица 2.3 – Результаты многократных взвешиваний золотого песка
| № варианта
| i
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| | 1
| m 1,г
| 421,1
| 421,3
| 421,2
| 421,4
| 421,3
| 421,2
| 421,5
| 421,6
| 421,4
| 421,2
| | m 2,г
| 425,3
| 425,1
| 425,7
| 425,5
| 425,0
| 424,9
| 425,3
| 425,4
| 425,6
| 425,7
| | 2
| m 1,г
| 521,1
| 521,3
| 521,2
| 521,4
| 521,3
| 521,2
| 521,5
| 521,6
| 521,4
| 521,2
| | m 2,г
| 525,3
| 525,1
| 525,7
| 525,5
| 525,0
| 524,9
| 525,3
| 525,4
| 525,6
| 525,7
| | 3
| m 1,г
| 621,1
| 621,3
| 621,2
| 621,4
| 621,3
| 621,2
| 621,5
| 621,6
| 621,4
| 621,2
| | m 2,г
| 625,3
| 625,1
| 625,7
| 625,5
| 625,0
| 624,9
| 625,3
| 625,4
| 625,6
| 625,7
| | 4
| m 1,г
| 721,1
| 721,3
| 721,2
| 721,4
| 721,3
| 721,2
| 721,5
| 721,6
| 721,4
| 721,2
| | m 2,г
| 725,3
| 725,1
| 725,7
| 725,5
| 725,0
| 724,9
| 725,3
| 725,4
| 725,6
| 725,7
| | 5
| m 1,г
| 221,1
| 221,3
| 221,2
| 221,4
| 221,3
| 221,2
| 221,5
| 221,6
| 221,4
| 221,2
| | m 2,г
| 225,3
| 225,1
| 225,7
| 225,5
| 225,0
| 224,9
| 225,3
| 225,4
| 225,6
| 225,7
| | 6
| m 1,г
| 321,1
| 321,3
| 321,2
| 321,4
| 321,3
| 321,2
| 321,5
| 321,6
| 321,4
| 321,2
| | m 2,г
| 325,3
| 325,1
| 325,7
| 325,5
| 325,0
| 324,9
| 325,3
| 325,4
| 325,6
| 325,7
| | 7
| m 1,г
| 751,1
| 751,2
| 751,0
| 749,9
| 750,0
| 751,4
| 751,8
| 751,5
| 751,4
| 751,3
| | m 2,г
| 743,6
| 743,4
| 743,2
| 743,6
| 743,4
| 743,2
| 743,1
| 743,9
| 743,0
| 743,6
| | 8
| m 1,г
| 651,1
| 651,2
| 651,0
| 649,9
| 650,0
| 651,4
| 651,8
| 651,5
| 651,4
| 651,3
| | m 2,г
| 643,6
| 643,4
| 643,2
| 643,6
| 643,4
| 643,2
| 643,1
| 643,9
| 643,0
| 643,6
| | 9
| m 1,г
| 551,1
| 551,2
| 551,0
| 549,9
| 550,0
| 551,4
| 551,8
| 551,5
| 551,4
| 551,3
| | m 2,г
| 543,6
| 543,4
| 543,2
| 543,6
| 543,4
| 543,2
| 543,1
| 543,9
| 543,0
| 543,6
| | 10
| m 1,г
| 451,1
| 451,2
| 451,0
| 449,9
| 450,0
| 451,4
| 451,8
| 451,5
| 451,4
| 451,3
| | m 2,г
| 443,6
| 443,4
| 443,2
| 443,6
| 443,4
| 443,2
| 443,1
| 443,9
| 443,0
| 443,6
| | 11
| m 1,г
| 351,1
| 351,2
| 351,0
| 349,9
| 350,0
| 351,4
| 351,8
| 351,5
| 351,4
| 351,3
| | m 2,г
| 343,6
| 343,4
| 343,2
| 343,6
| 343,4
| 343,2
| 343,1
| 343,9
| 343,0
| 343,6
| | 12
| m 1,г
| 251,1
| 251,2
| 251,0
| 249,9
| 250,0
| 251,4
| 251,8
| 251,5
| 251,4
| 251,3
| | m 2,г
| 243,6
| 243,4
| 243,2
| 243,6
| 243,4
| 243,2
| 243,1
| 243,9
| 243,0
| 243,6
| | 13
| m 1,г
| 151,1
| 151,2
| 151,0
| 149,9
| 150,0
| 151,4
| 151,8
| 151,5
| 151,4
| 151,3
| | m 2,г
| 143,6
| 143,4
| 143,2
| 143,6
| 143,4
| 143,2
| 143,1
| 143,9
| 143,0
| 143,6
| | 14
| m 1,г
| 391,2
| 391,3
| 391,0
| 391,4
| 391,8
| 391,4
| 391,5
| 391,2
| 391,5
| 391,7
| | m 2,г
| 399,0
| 399,5
| 399,2
| 398,9
| 399,3
| 399,4
| 399,2
| 399,1
| 399,0
| 398,8
| | 15
| m 1,г
| 291,2
| 291,3
| 291,0
| 291,4
| 291,8
| 291,4
| 291,5
| 291,2
| 291,5
| 291,7
| | m 2,г
| 299,0
| 299,5
| 299,2
| 298,9
| 299,3
| 299,4
| 299,2
| 299,1
| 299,0
| 298,8
| | 16
| m 1,г
| 191,2
| 191,3
| 191,0
| 191,4
| 191,8
| 191,4
| 191,5
| 191,2
| 191,5
| 191,7
| | m 2,г
| 199,0
| 199,5
| 199,2
| 198,9
| 199,3
| 199,4
| 199,2
| 199,1
| 199,0
| 198,8
| | 17
| m 1,г
| 491,2
| 491,3
| 491,0
| 491,4
| 491,8
| 491,4
| 491,5
| 491,2
| 491,5
| 491,7
| | m 2,г
| 499,0
| 499,5
| 499,2
| 498,9
| 499,3
| 499,4
| 499,2
| 499,1
| 499,0
| 498,8
| | 18
| m 1,г
| 751,1
| 751,2
| 751,0
| 749,9
| 750,0
| 751,4
| 751,8
| 751,5
| 751,4
| 751,3
| | m 2,г
| 743,6
| 743,4
| 743,2
| 743,6
| 743,4
| 743,2
| 743,1
| 743,9
| 743,0
| 743,6
| | 19
| m 1,г
| 621,1
| 621,3
| 621,2
| 621,4
| 621,3
| 621,2
| 621,5
| 621,6
| 621,4
| 621,2
| | m 2,г
| 625,3
| 625,1
| 625,7
| 625,5
| 625,0
| 624,9
| 625,3
| 625,4
| 625,6
| 625,7
| | 20
| m 1,г
| 221,1
| 221,3
| 221,2
| 221,4
| 221,3
| 221,2
| 221,5
| 221,6
| 221,4
| 221,2
| | m 2,г
| 225,3
| 225,1
| 225,7
| 225,5
| 225,0
| 224,9
| 225,3
| 225,4
| 225,6
| 225,7
| | 21
| m 1,г
| 21,1
| 21,3
| 21,2
| 21,4
| 21,3
| 21,2
| 21,5
| 21,6
| 21,4
| 21,2
| | m 2,г
| 25,3
| 25,1
| 25,7
| 25,5
| 25,0
| 24,9
| 25,3
| 25,4
| 25,6
| 25,7
| | 22
| m 1,г
| 851,1
| 851,2
| 851,0
| 849,9
| 850,0
| 851,4
| 851,8
| 851,5
| 851,4
| 851,3
| | m 2,г
| 843,6
| 843,4
| 843,2
| 843,6
| 843,4
| 843,2
| 843,1
| 843,9
| 843,0
| 843,6
| | 23
| m 1,г
| 891,2
| 891,3
| 891,0
| 891,4
| 891,8
| 891,4
| 891,5
| 891,2
| 891,5
| 891,7
| | m 2,г
| 899,0
| 899,5
| 899,2
| 898,9
| 899,3
| 899,4
| 899,2
| 899,1
| 899,0
| 898,8
| | 24
| m 1,г
| 951,1
| 951,2
| 951,0
| 949,9
| 950,0
| 951,4
| 951,8
| 951,5
| 951,4
| 951,3
| | m 2,г
| 943,6
| 943,4
| 943,2
| 943,6
| 943,4
| 943,2
| 943,1
| 943,9
| 943,0
| 943,6
| | 25
| m 1,г
| 111,1
| 115,6
| 114,9
| 114,8
| 114,3
| 115,1
| 115,4
| 115,1
| 114,6
| 114,9
| | m 2,г
| 116,1
| 116,4
| 116,1
| 115,6
| 115,9
| 116,1
| 116,6
| 116,9
| 116,8
| 116,3
| | 26
| m 1,г
| 211,1
| 215,6
| 214,9
| 214,8
| 214,3
| 215,1
| 215,4
| 215,1
| 214,6
| 214,9
| | m 2,г
| 216,1
| 216,4
| 216,1
| 215,6
| 215,9
| 216,1
| 216,6
| 216,9
| 216,8
| 216,3
| | 27
| m 1,г
| 311,1
| 315,6
| 314,9
| 314,8
| 314,3
| 315,1
| 315,4
| 315,1
| 314,6
| 314,9
| | m 2,г
| 316,1
| 316,4
| 316,1
| 315,6
| 315,9
| 316,1
| 316,6
| 316,9
| 316,8
| 316,3
| | 28
| m 1,г
| 415,1
| 415,4
| 415,1
| 414,6
| 414,9
| 411,1
| 415,6
| 414,9
| 414,8
| 414,3
| | m 2,г
| 416,1
| 416,6
| 416,9
| 416,8
| 416,3
| 416,1
| 416,4
| 416,1
| 415,6
| 415,9
| | 29
| m 1,г
| 511,1
| 515,6
| 514,9
| 514,8
| 514,3
| 515,1
| 515,4
| 515,1
| 514,6
| 514,9
| | m 2,г
| 516,1
| 516,4
| 516,1
| 515,6
| 515,9
| 516,1
| 516,6
| 516,9
| 516,8
| 516,3
| | 30
| m 1,г
| 615,1
| 615,4
| 615,1
| 614,6
| 614,9
| 611,1
| 615,6
| 614,9
| 614,8
| 614,3
| | m 2,г
| 616,1
| 616,6
| 616,9
| 616,8
| 616,3
| 616,1
| 616,4
| 616,1
| 615,6
| 615,9
| | 31
| m 1,г
| 51,1
| 51,2
| 51,0
| 49,9
| 50,0
| 51,4
| 51,8
| 51,5
| 51,4
| 51,3
| | m 2,г
| 43,6
| 43,4
| 43,2
| 43,6
| 43,4
| 43,2
| 43,1
| 43,9
| 43,0
| 43,6
| | 32
| m 1,г
| 21,1
| 21,3
| 21,2
| 21,4
| 21,3
| 21,2
| 21,5
| 21,6
| 21,4
| 21,2
| | m 2,г
| 25,3
| 25,1
| 25,7
| 25,5
| 25,0
| 24,9
| 25,3
| 25,4
| 25,6
| 25,7
| | 33
| m 1,г
| 91,2
| 91,3
| 91,0
| 91,4
| 91,8
| 91,4
| 91,5
| 91,2
| 91,5
| 91,7
| | m 2,г
| 99,0
| 99,5
| 99,2
| 98,9
| 99,3
| 99,4
| 99,2
| 99,1
| 99,0
| 98,8
| | 34
| m 1,г
| 67,7
| 67,4
| 67,3
| 67,8
| 67,9
| 67,5
| 67,2
| 67,6
| 67,7
| 67,4
| | m 2,г
| 64,5
| 64,6
| 64,2
| 64,8
| 64,7
| 64,3
| 64,9
| 64,5
| 64,7
| 64,8
| | 35
| m 1,г
| 167,5
| 167,2
| 167,6
| 167,7
| 167,4
| 167,7
| 167,4
| 167,3
| 167,8
| 167,9
| | m 2,г
| 164,3
| 164,9
| 164,5
| 164,7
| 164,8
| 164,5
| 164,6
| 164,2
| 164,8
| 164,7
| | 36
| m 1,г
| 267,7
| 267,4
| 267,3
| 267,8
| 267,9
| 267,5
| 267,2
| 267,6
| 267,7
| 267,4
| | m 2,г
| 264,5
| 264,6
| 264,2
| 264,8
| 264,7
| 264,3
| 264,9
| 264,5
| 264,7
| 264,8
| | 37
| m 1,г
| 367,5
| 367,2
| 367,6
| 367,7
| 367,4
| 367,7
| 367,4
| 367,3
| 367,8
| 367,9
| | m 2,г
| 364,3
| 364,9
| 364,5
| 364,7
| 364,8
| 364,5
| 364,6
| 364,2
| 364,8
| 364,7
| | 38
| m 1,г
| 467,7
| 467,4
| 467,3
| 467,8
| 467,9
| 467,5
| 467,2
| 467,6
| 467,7
| 467,4
| | m 2,г
| 464,5
| 464,6
| 464,2
| 464,8
| 464,7
| 464,3
| 464,9
| 464,5
| 464,7
| 464,8
| | 39
| m 1,г
| 991,2
| 991,3
| 991,0
| 991,4
| 991,8
| 991,4
| 991,5
| 991,2
| 991,5
| 991,7
| | m 2,г
| 999,0
| 999,5
| 999,2
| 998,9
| 999,3
| 999,4
| 999,2
| 999,1
| 999,0
| 998,8
| | 40
| m 1,г
| 567,3
| 567,8
| 567,9
| 567,5
| 567,2
| 567,6
| 567,7
| 567,4
| 567,7
| 567,4
| | m 2,г
| 564,2
| 564,8
| 564,7
| 564,3
| 564,9
| 564,5
| 564,7
| 564,8
| 564,5
| 564,6
|
Задание 2.3.4
Определить величину рассеиваемой мощности на элементе электрической цепи (сопротивление элемента цепи 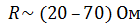 ) при протекании через него постоянного тока. Результаты многократных измерений тока и напряжения на элементе представлены в таблице 2.4. ) при протекании через него постоянного тока. Результаты многократных измерений тока и напряжения на элементе представлены в таблице 2.4.
Характеристики цифрового вольтметра:
- входное сопротивление, Rv =10 МОм;
- приведенная погрешность, γu = 0,2%,
- верхний предел диапазона измерений, U в = 10 В.
Характеристики цифрового вольтметра, работающего в режиме амперметра:
- входное сопротивление 0,01 Ом;
- приведенная погрешность, γI = 0,1%,
- верхний предел диапазона измерений, I в = 200 мА.
Относительная дополнительная погрешность, δдоп, для обоих режимов вольтметра описывается выражением:
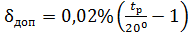 , ,
где t р – температура окружающей среды.
Условия измерения: t р= 300 С; доверительная вероятность P = 0,95.
Результаты измерения в таблице 2.4 относятся к нормальномураспределению.
Таблица 2.4 – Результаты многократных измерений U и I
| № варианта
| i
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| | 1
| U, В
| 2,432
| 2,430
| 2,421
| 2,429
| 2,435
| 2,491
| 2,435
| 2,434
| | I, мА
| 47,35
| 47,33
| 47,40
| 47,39
| 47,30
| 47,98
| 47,29
| 47,31
| | 2
| U, В
| 2,332
| 2,330
| 2,321
| 2,329
| 2,335
| 2,3 91
| 2,335
| 2,334
| | I, мА
| 46,35
| 46,33
| 46,40
| 46,39
| 46,30
| 46,98
| 46,29
| 46,31
| | 3
| U, В
| 2,302
| 2,300
| 2,301
| 2,309
| 2,315
| 2,3 31
| 2,305
| 2,304
| | I, мА
| 46,05
| 46,03
| 46,00
| 46,09
| 46,00
| 46,48
| 46,09
| 46,01
| | 4
| U, В
| 2,132
| 2,130
| 2,121
| 2,129
| 2,135
| 2,1 91
| 2,135
| 2,134
| | I, мА
| 45,35
| 45,33
| 45,40
| 45,39
| 45,30
| 45,98
| 45,29
| 45,31
| | 5
| U, В
| 2,032
| 2,030
| 2,021
| 2,029
| 2,035
| 2,0 91
| 2,035
| 2,034
| | I, мА
| 44,35
| 44,33
| 44,40
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| | 6
| U, В
| 1,535
| 1,533
| 1,534
| 1,501
| 1,535
| 1,539
| 1,537
| 1,536
| | I, мА
| 35,75
| 35,77
| 35,74
| 34,28
| 35,70
| 35,77
| 35,74
| 35,77
| | 7
| U, В
| 1,585
| 1,583
| 1,584
| 1,541
| 1,585
| 1,589
| 1,587
| 1,586
| | I, мА
| 36,75
| 36,77
| 36,74
| 35,28
| 36,70
| 36,77
| 36,74
| 36,77
| | 8
| U, В
| 1,535
| 1,533
| 1,534
| 1,501
| 1,535
| 1,539
| 1,537
| 1,536
| | I, мА
| 36,75
| 36,77
| 36,74
| 35,28
| 36,70
| 36,77
| 36,74
| 36,77
| | 9
| U, В
| 1,585
| 1,583
| 1,584
| 1,541
| 1,585
| 1,589
| 1,587
| 1,586
| | I, мА
| 44,35
| 44,33
| 44,40
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| | 10
| U, В
| 2,132
| 2,130
| 2,121
| 2,129
| 2,135
| 2,1 91
| 2,135
| 2,134
| | I, мА
| 47,35
| 47,33
| 47,40
| 47,39
| 47,30
| 47,98
| 47,29
| 47,31
| | 11
| U, В
| 1.201
| 1,205
| 1,208
| 1,209
| 1,211
| 1,202
| 1,211
| 1,209
| | I, мА
| 25,67
| 25.60
| 25,60
| 24,21
| 25,70
| 25,67
| 25,60
| 25,65
| | 12
| U, В
| 1,107
| 1,101
| 1,111
| 1,109
| 1,112
| 1,102
| 1,087
| 1,105
| | I, мА
| 22,23
| 22,27
| 22,29
| 22,22
| 22,18
| 22,32
| 22,31
| 22,00
| | 13
| U, В
| 2,032
| 2,030
| 2,021
| 2,029
| 2,035
| 2,0 91
| 2,035
| 2,034
| | I, мА
| 25,67
| 25.60
| 25,60
| 24,21
| 25,70
| 25,67
| 25,60
| 25,65
| | 14
| U, В
| 1,535
| 1,533
| 1,534
| 1,501
| 1,535
| 1,539
| 1,537
| 1,536
| | I, мА
| 47,35
| 47,33
| 47,40
| 47,39
| 47,30
| 47,98
| 47,29
| 47,31
| | 15
| U, В
| 1,107
| 1,101
| 1,111
| 1,109
| 1,112
| 1,102
| 1,087
| 1,105
| | I, мА
| 45,35
| 45,33
| 45,40
| 45,39
| 45,30
| 45,98
| 45,29
| 45,31
| | 16
| U, В
| 1.201
| 1,205
| 1,208
| 1,209
| 1,211
| 1,202
| 1,211
| 1,209
| | I, мА
| 36,75
| 36,77
| 36,74
| 35,28
| 36,70
| 36,77
| 36,74
| 36,77
| | 17
| U, В
| 0,981
| 0,986
| 0,981
| 0,985
| 0,972
| 0,987
| 0,989
| 0,984
| | I, мА
| 15,67
| 15,61
| 15,69
| 15,72
| 15,45
| 15,66
| 15,59
| 15,61
| | 18
| U, В
| 1,585
| 1,583
| 1,584
| 1,541
| 1,585
| 1,589
| 1,587
| 1,586
| | I, мА
| 22,23
| 22,27
| 22,29
| 22,22
| 22,18
| 22,32
| 22,31
| 22,00
| | 19
| U, В
| 2,432
| 2,430
| 2,421
| 2,429
| 2,435
| 2,491
| 2,435
| 2,434
| | I, мА
| 25,67
| 25.60
| 25,60
| 24,21
| 25,70
| 25,67
| 25,60
| 25,65
| | 20
| U, В
| 0,981
| 0,986
| 0,981
| 0,985
| 0,972
| 0,987
| 0,989
| 0,984
| | I, мА
| 44,35
| 44,33
| 44,40
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| | 21
| U, В
| 3,432
| 3,430
| 3,421
| 3,429
| 3,435
| 3,491
| 3,435
| 3,434
| | I, мА
| 7,35
| 7,33
| 7,40
| 7,39
| 7,30
| 7,98
| 7,29
| 7,31
| | 22
| U, В
| 3,332
| 3,330
| 3,321
| 3,329
| 3,335
| 3,3 91
| 3,335
| 3,334
| | I, мА
| 146,35
| 146,33
| 146,40
| 146,39
| 146,30
| 146,98
| 146,29
| 146,31
| | 23
| U, В
| 4,302
| 4,300
| 4,301
| 4,309
| 4,315
| 4,3 31
| 4,305
| 4,304
| | I, мА
| 146,05
| 146,03
| 146,00
| 146,09
| 146,00
| 146,48
| 146,09
| 146,01
| | 24
| U, В
| 4,132
| 4,130
| 4,121
| 4,129
| 4,135
| 4,1 91
| 4,135
| 4,134
| | I, мА
| 45,35
| 45,33
| 45,40
| 45,39
| 45,30
| 45,98
| 45,29
| 45,31
| | 25
| U, В
| 5,032
| 5,030
| 5,021
| 5,029
| 5,035
| 5,0 91
| 5,035
| 5,034
| | I, мА
| 44,35
| 44,33
| 44,40
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| | 26
| U, В
| 5,535
| 5,533
| 5,534
| 5,501
| 5,535
| 5,539
| 5,537
| 5,536
| | I, мА
| 35,75
| 35,77
| 35,74
| 34,28
| 35,70
| 35,77
| 35,74
| 35,77
| | 27
| U, В
| 5,585
| 5,583
| 5,584
| 5,541
| 5,585
| 5,589
| 5,587
| 5,586
| | I, мА
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| 44,35
| 44,33
| 44,40
| | 28
| U, В
| 6,132
| 6,130
| 6,121
| 6,129
| 6,135
| 6,1 91
| 6,135
| 6,134
| | I, мА
| 47,35
| 47,33
| 47,40
| 47,39
| 47,30
| 47,98
| 47,29
| 47,31
| | 29
| U, В
| 6,107
| 6,101
| 6,111
| 6,109
| 6,112
| 6,102
| 6,087
| 6,105
| | I, мА
| 45,35
| 45,33
| 45,40
| 45,39
| 45,30
| 45,98
| 45,29
| 45,31
| | 30
| U, В
| 7,432
| 7,430
| 7,421
| 7,429
| 7,435
| 7,491
| 7,435
| 7,434
| | I, мА
| 25,67
| 25.60
| 25,60
| 24,21
| 25,70
| 25,67
| 25,60
| 25,65
| | 31
| U, В
| 2,432
| 2,430
| 2,421
| 2,429
| 2,435
| 2,491
| 2,435
| 2,434
| | I, мА
| 0,2654
| 0,2651
| 0,2601
| 0,2657
| 0,2650
| 0,2659
| 0,2661
| 0,2658
| | 32
| U, В
| 2,332
| 2,330
| 2,321
| 2,329
| 2,335
| 2,3 91
| 2,335
| 2,334
| | I, мА
| 0,3561
| 0,3560
| 0,3569
| 0,3571
| 0,3589
| 0,3562
| 0,3564
| 0,3566
| | 33
| U, В
| 2,302
| 2,300
| 2,301
| 2,309
| 2,315
| 2,3 31
| 2,305
| 2,304
| | I, мА
| 0,432
| 0,430
| 0,421
| 0,429
| 0,435
| 0,491
| 0,435
| 0,434
| | 34
| U, В
| 45,35
| 45,33
| 45,40
| 45,39
| 45,30
| 45,98
| 45,29
| 45,31
| | I, мА
| 47,35
| 47,33
| 47,40
| 47,39
| 47,30
| 47,98
| 47,29
| 47,31
| | 35
| U, В
| 35,75
| 35,77
| 35,74
| 34,28
| 35,70
| 35,77
| 35,74
| 35,77
| | I, мА
| 1,535
| 1,533
| 1,534
| 1,501
| 1,535
| 1,539
| 1,537
| 1,536
| | 36
| U, В
| 44,39
| 44,30
| 44,98
| 44,29
| 44,31
| 44,35
| 44,33
| 44,40
| | I, мА
| 6,107
| 6,101
| 6,111
| 6,109
| 6,112
| 6,102
| 6,087
| 6,105
| | 37
| U, В
| 146,05
| 146,03
| 146,00
| 146,09
| 146,00
| 146,48
| 146,09
| 146,01
| | I, мА
| 5,032
| 5,030
| 5,021
| 5,029
| 5,035
| 5,0 91
| 5,035
| 5,034
| | 38
| U, В
| 25,67
| 25.60
| 25,60
| 24,21
| 25,70
| 25,67
| 25,60
| 25,65
| | I, |
|



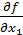 ,
, 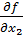 ,
,  , …
, … 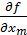
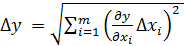 . (2.2)
. (2.2)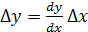 . (2.3)
. (2.3)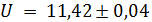 [В];
[В]; 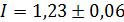 [мA] для Р = 0,95.
[мA] для Р = 0,95.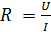 .
.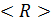 :
: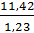 = 9,285 [кОм].
= 9,285 [кОм].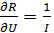 ;
; 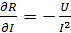 .
.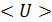 ( 11,42 В) и
( 11,42 В) и 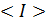 (1,23 мА):
(1,23 мА):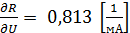 ,
, 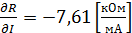 .
.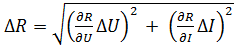 =
= 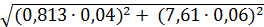 = 0,458 [кОм].
= 0,458 [кОм].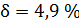 .
.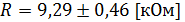 для Р = 0,95;
для Р = 0,95;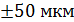 .
.
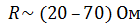 ) при протекании через него постоянного тока. Результаты многократных измерений тока и напряжения на элементе представлены в таблице 2.4.
) при протекании через него постоянного тока. Результаты многократных измерений тока и напряжения на элементе представлены в таблице 2.4.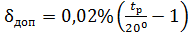 ,
,


