
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка случайной погрешностиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для того, чтобы оценить величину случайной погрешности, один и тот же опыт (измерение) необходимо повторить несколько раз. Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений: 1) погрешности измерений могут принимать непрерывный ряд значений; 2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто, 3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.
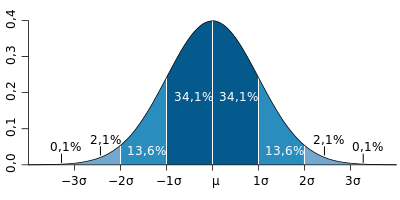
Рис. П1.2 – График нормального закона распределения Гаусса
Если число отклонений от среднего значения всех результатов измерения (многочисленных измерений) конкретной физической величины поместить под кривую Гаусса, то, как видно на рис. П2, 68,2% всех измерений расположится в доверительном интервале 2 σ. При доверительном интервале, равном 6 σ, внутри этого интервала окажется 99,7% всех измерений (доверительная вероятность равна 0,997). По этой причине полуширину доверительного интервала (6 σ), 3 σ, называют предельной случайной погрешностью. Уравнение кривой Гаусса имеет вид:
где Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений. Точное значение среднеквадратичной погрешности σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой среднеквадратичная погрешность равняется средней квадратичной ошибке среднего арифметического
где Чем больше число измерений, тем меньше
Распределение вероятностей этой величины не зависит от σ2, а существенно зависит от числа опытов n. С увеличением числа опытов n распределение Стьюдента стремится к распределению Гаусса. Функция распределения табулирована. Систематическая погрешность средства измерений – составляющая погрешности средства измерений, принимаемая за постоянную или закономерную изменяющуюся. Чаще всего систематические погрешности соответствуют отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: 1) несоответствие средств измерения эталону (например, линейка с «неправильной» шкалой, «спешащий» или «отстающий» секундомер и т.п.); 2) неправильная установка измерительных приборов (наклон, неуравновешенность); 3) несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; 4) несоответствие измеряемого объекта с предположением о его свойствах (наличие пустот и т.п.); 5) отличие условий эксперимента от теоретических представлений об исследуемом процессе (например, при взвешивании тел не учитывается действия на них силы Архимеда); 6) игнорирование изменений, которые происходят во внешней обстановке (например, колебаний температуры или атмосферного давления). По возможности исключения систематические погрешности подразделяются на исключаемые и неисключаемые. Исключаемые погрешности – это такие погрешности, которые можно определить, а затем и исключить их влияние на результат измерения. Например, после проведения измерений с помощью цифрового вольтметра было установлено, что не выставлен «ноль» вольтметра. Начальное смещение (около нуля) – систематическая погрешность. Путем вычитания начального смещения из результата измерения эта погрешность исключается. Грубая погрешность (промах) – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором. К ним можно отнести: неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы; неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь; хаотические изменения параметров питающего средства измерения напряжения, например, его амплитуды или частоты; незамеченные неисправности аппаратуры (средства измерения). Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений По источнику возникновения погрешности делятся на инструментальные и методические. Инструментальной называется погрешность, обусловленная свойствами используемого средства измерения. Она вызвана тем, что абсолютно точных приборов не существует. Их показания всегда отличаются от истинного значения. Инструментальные погрешности относят к систематическим погрешностям. Различают несколько составляющих инструментальной погрешности: основную, дополнительную и обусловленную взаимодействием средств и объекта измерений. Погрешности, имеющие место при нормальных условиях применения средств измерений (температуре 296 К, определенной влажности, атмосферном давлении 760 мм рт. ст. и т.п.), называются основными; погрешности, вызванные отклонениями от нормальных условий, влияющих на результат измерений, называются дополнительными. У большинства средств измерений информация о предельном значении основной инструментальной погрешности содержится в классе точности (указывается на шкале стрелочного прибора или в его паспорте). Классом точности или приведенной погрешностью, γ, называется выраженное в процентах отношение максимально возможной абсолютной основной инструментальной погрешности
Классы точности присваиваются средствам измерений с учетом результатов государственных приемочных испытаний. Если класс точности неизвестен, то основную инструментальную погрешность принимают равной половине цены деления шкалы измерительного средства. Зная класс точности, можно найти максимальную абсолютную основную погрешность средства измерения:
Погрешности, обусловленные взаимодействием средства и объекта измерения. Подключение к исследуемому объекту средства измерений в ряде случаях приводит к изменению значения регистрируемой величины. Например, амперметр, включаемый в электрическую цепь для измерения силы тока, всегда обладает конечным внутренним сопротивлением, что изменяет полное сопротивление цепи и силу тока, текущего в ней. Эта составляющая инструментальной погрешности зависит от свойств средства и объекта измерений. Пример. Измерить напряжение в базовой цепи каскада на транзисторе VT (см. рисунок, не учитывая сопротивлений эмиттерной и коллекторной цепей).
Действительное напряжение в точке А:
Измеренное значение напряжения в точке А при подключении вольтметра:
При этом погрешность взаимодействия составит 33 %:
В случае использования вольтметра с входным сопротивлением 1МОм погрешность взаимодействия составит 4,7 %. Таким образом, неправильный выбор измерительного прибора приводит не только к значительным погрешностям взаимодействия, но и нарушает режимы работы объекта измерения. Отсюда вытекает один из основных принципов измерений: средство измерения должно оказывать минимально возможное влияние на объект измерения.
Методические погрешности могут возникнуть из-за несовершенства выбранного метода измерений, ограниченной точности эмпирических формул, применяемых для описания явления, положенного в основу измерения, а также ограниченной точности используемых в уравнениях физических констант. Сюда же следует отнести и погрешности, обусловленные несоответствием принятой модели измерений реальному объекту вследствие принятых допущений или упрощений. В некоторых случаях влияние этих допущений на погрешность измерений оказывается незначительным, в других оно может оказаться существенным. Примером погрешности, обусловленной упрощением метода измерений, является пренебрежение массой воздуха, вытесненного, согласно закону Архимеда, гирей при взвешивании на рычажных весах. При проведении рабочих измерений ею, как правило, пренебрегают. Однако при точных измерениях с нею приходится считаться, при этом вносится соответствующая поправка. Другим примером является измерение объемов тел, форма которых принимается (в модели измерений) геометрически правильной, путем измерения недостаточного числа линейных размеров. Так, существенную методическую погрешность будет иметь результат измерения объема помещения путем измерения одной длины, одной ширины и одной высоты. Для более точного измерения объема следовало бы измерить эти параметры по каждой стене в нескольких местах. Методические погрешности относятся к систематическим погрешностям. Для того, чтобы оценить полную погрешность измерения конкретной физической величины исследуемого объекта, необходимо владеть методикой оценки всех выше рассмотренных составляющих этой погрешности.
ПРИЛОЖЕНИЕ 2
|
|||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.006 с.) |

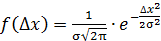 ,
,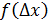 - функция распределения случайных погрешностей, характеризующая вероятность появления погрешности
- функция распределения случайных погрешностей, характеризующая вероятность появления погрешности 
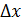 , σ – среднеквадратичное значение погрешности.
, σ – среднеквадратичное значение погрешности.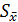 , величина которой определяется по формуле:
, величина которой определяется по формуле: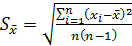 ,
,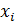 - результат i -го измерения;
- результат i -го измерения; 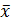 - среднее арифметическое полученных значений; n - число измерений.
- среднее арифметическое полученных значений; n - число измерений.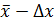 до
до 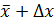 , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку
, в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку 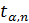 , называемое коэффициентом Стьюдента, дает значение доверительного интервала
, называемое коэффициентом Стьюдента, дает значение доверительного интервала 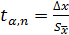 . (П1.1)
. (П1.1)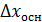 к верхнему пределу измерений (верхнее значение шкалы измерения) xmax:
к верхнему пределу измерений (верхнее значение шкалы измерения) xmax: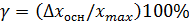 . (П1.2)
. (П1.2)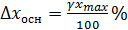 . (П1.3)
. (П1.3)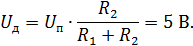
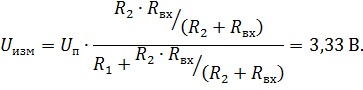
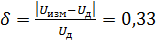 .
.


