Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов совместных измерений
Совместные измерения – это производимые одновременно измерения двух или нескольких разнородных величин для нахождения зависимостей между ними.
Рекомендации при обработке совместных измерений. Метод наименьших квадратов Целью совместных измерений является нахождение зависимости между несколькими прямо или косвенно измеренными величинами. Надежным и научно обоснованным способом определения коэффициентов экспериментальных зависимостей является метод наименьших квадратов (МНК). Суть его заключается в подборе таких значений коэффициентов, при которых сумма квадратов отклонений, измеренных в опытах значений yi (i =1,2,…, n) от рассчитанных была бы минимальной. МНК позволяет не только найти коэффициенты функциональной зависимости, но и провести оценку погрешностей найденных коэффициентов.
МНК рассмотрим в варианте, когда приняты следующие допущения: - между переменными существует зависимость вида y = a + bx; - погрешности величины x малы.
Расчет коэффициентов a и b следует проводить в такой последовательности:
1. Из опыта получить n пар значений аргумента и функции (xi, yi ).
2. Найти средние значения всех экспериментальных точек:
3. Найти коэффициенты прямой по следующим формулам:
4. Рассчитать параметры di, D по следующим формулам:
5. Определить среднеквадратичное отклонение (СКО) коэффициентов a и b:
Расчет коэффициента b и его СКО упрощается, если из теории известно, что прямая проходит через начало координат. Тогда параметр b и его СКО находят по следующим формулам:
6. Погрешность рассчитанной величины y при произвольном значении аргумента x рассчитывают для доверительной вероятности α = 0,95 как погрешность косвенных измерений:
Примеры обработки результатов совместных измерений Пример 1 Исследуется зависимость скорости V(t) при равноускоренном движении, которая удовлетворяет уравнению прямой V = V 0 + gt.
Результаты измерений представлены в табл. 4.1.
Таблица 4.1 – Результаты измерений
Решение. 1. По формулам (4.1) находим средние значения:
2. Затем по формулам (4.2) рассчитываем значения искомых параметров:
3. Далее по формулам (4.3) – (4.5) находим вспомогательные параметры и СКО коэффициентов:
4. Для доверительной вероятности α=0,95 находим границы доверительных интервалов коэффициентов по формуле (4.6):
5. Результат измерения с учетом правил представления результатов измерения записываем в виде: V 0 = a = (2,1± 0,6) м/с; g = b = (0,98± 0,08)м/с2 ,
а искомое уравнение выглядит следующим образом:
V = 2,1+ 0,98 t.
Следует отметить, что из-за сравнительно большого объема вычислений применение метода наименьших квадратов целесообразно проводить с помощью компьютера. Пример 2. Алгоритм обработки данных по МНК для уравнения Рассмотрим эксперимент по определению скорости тела
Таблица 4.2 – Результаты обработки эксперимента
Решение. 1. Средние значения
2. Среднее значение
3. Дисперсия и СКО
4. Дисперсия и СКО
5. Случайные погрешности Коэффициент Стьюдента для Р = 95 % и N – 1 = 5 равен
6. Инструментальная погрешность коэффициента
где учтено, что
7. Полные погрешности
8. Результат:
9. Окончательный результат в округленной форме:
Пример 3. Алгоритм обработки данных по МНК для уравнения y = ax на примере определения ускорения свободного падения
Рассмотрим эксперимент по определению ускорения свободного падения
Таблица 4.3 – Результаты обработки эксперимента
Дальнейшая обработка данных осуществляется в следующей последовательности. 1. Линеаризуем зависимость В новых переменных она будет иметь вид y = ax.
2. Заполняем табл. 4.4 обработки данных по МНК для уравнения y = ax, представив исходные данные в новых переменных
Таблица 4.4 – Результаты обработки данных по МНК
3. Среднее значение:
4. Дисперсия и СКО
5. Случайная погрешность коэффициента
6. Инструментальная погрешность измеряемой прямым образом величины у = Т равна:
7. Используя данные табл. 4.3, 4.4, получим:
8. Тогда инструментальная погрешность коэффициента
9. Полная погрешность коэффициента
10. Результат измерения в округленной форме:
По коэффициенту
11. Среднее значение:
12. Случайная погрешность:
13. Инструментальная погрешность:
14. Полная погрешность:
15. Окончательный результат в округленной форме:
Задания по обработке результатов совместных измерений Обработать результаты и записать конечные результаты измерений. Задание 4.3.1. Найдите по МНК коэффициент a в уравнении у = ax и коэффициенты а и b в уравнении y = ax + b по известным значениям координат (xi, yi). Значения координаты xi приведены в первой строке таблицы и предполагаются для всех наборов y одинаковыми. Первая строка уi в каждом варианте описывается уравнением у = aх, вторая – уравнением у = ax + b. Приборные погрешности θ x = 0.05, θ y = 0.005. Постройте экспериментальные точки и рассчитанную регрессионную прямую на одном графике.
Таблица 4.5 – Исходные данные
Задание 4.3.2 В эксперименте получено пять измерений величин x и y, результаты которых приведены в таблице 4.6. Известно, что уравнение измерения имеет вид Таблица 4.6 – Результаты измерений величин x и y
ПРИЛОЖЕНИЕ 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.073 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; 
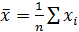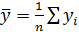. (4.1)
; 
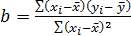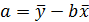. (4.2)
; 
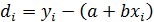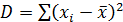. (4.1.3)
; 
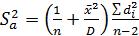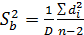. (4.4)
; 
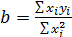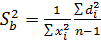. (4.5)
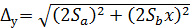. (4.6)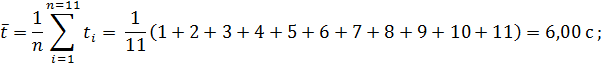
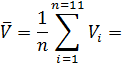
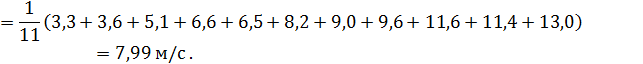
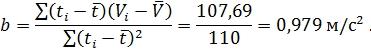
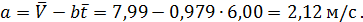
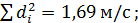
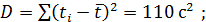
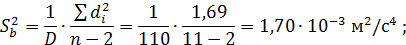
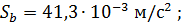
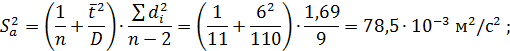
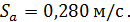
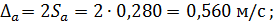
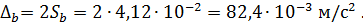
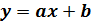на примере определения параметров равноускоренного движения
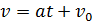при равноускоренном движении, по результатам которого надо найти ускорение тела а и его начальную скорость v 0. Пусть инструментальные погрешности определения времени и скорости равны, соответственно, 
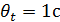и 
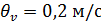. Результаты обработки эксперимента согласно МНК сведены в таблицу 4.2.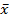
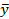
xi =75
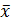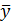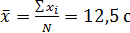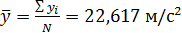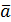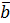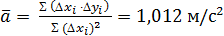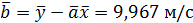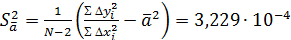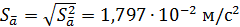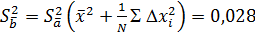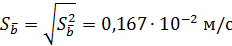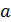и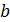 
:
, 
.
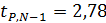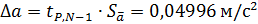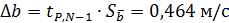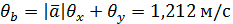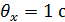и 
:
, 
.
, 
.
, 
.
и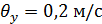 
.
, 
, 
.
,
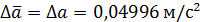и 
.
и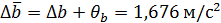 
.
.
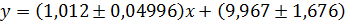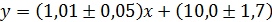с вероятностью P = 95 %.
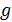по совместным измерениям периода колебания математического маятника Т и его длины l, значения которых даются в табл. 4.3.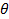
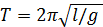, положив 
.
. 
.
:
, 
.
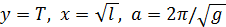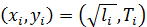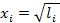
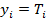
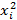
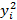
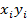
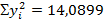
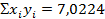
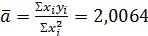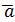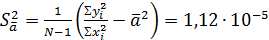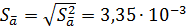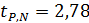, имеет вид:
.
.
, 
.
.
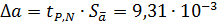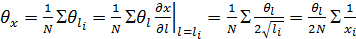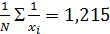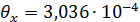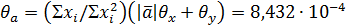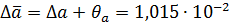
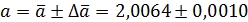с вероятностью P = 95 %.
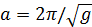может быть найдено ускорение свободного падения 
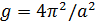по стандартной схеме обработки данных косвенных измерений методом переноса погрешностей.
.
.
.
.
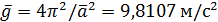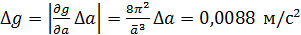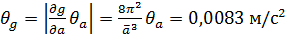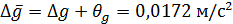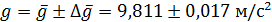с вероятностью P = 95 %.
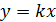. Используя метод наименьших квадратов, рассчитать наилучшее значение коэффициента k и погрешность 
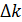, с которой этот коэффициент определен. Построить наилучшую прямую.
