
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок обработки результатов прямых измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Когда физическая величина а определяется непосредственно с помощью того или иного измерительного прибора (прямые измерения), оценка истинного значения измеряемой величины и погрешности может быть осуществлена в следующем порядке: 1. Составляется таблица результатов измерений. 2.
Вычисляется среднеарифметическое значение из n измерений: 3. Определяются погрешности отдельных измерений:
4. 5. Вычисляется средняя квадратичная погрешность результата серии измерений:
6. Если имеются резко отличающиеся от остальных значения, выясняют, не являются ли они промахами. 7. Задаются значением доверительной вероятности a (в лабораторных работах физического практикума обычно принимают a в пределах от 0,8 до 0,9). 8. Определяют по таблице 2 коэффициент Стьюдента t (a, n) для заданной надежности a и числа проведенных 9. Определяют границы доверительного интервала:
10. Рассчитывают относительную погрешность результата серии измерений:
11. Окончательный результат записывается в виде:
Расчет погрешностей косвенных измерений Как уже указывалось, косвенные измерения физической величины определяются прямыми измерениями других физических величин, которые находятся в определенной функциональной зависимости от искомой величины. Для определения надежности результата косвенных измерений необходимо применять распределение вероятностей рассматриваемой функции. Однако, такой строгий подход во многих случаях можно заменить упрощенным. Пусть искомая величина Х является функцией только одной переменной, т.е.
откуда
Заменяя значок дифференциала d значком ошибки D, получаем формулу для абсолютной погрешности результата косвенных измерений:
Окончательный результат можно представить в виде:
Относительная погрешность равна:
Пусть Х является функцией нескольких переменных, т.е. X = f (x, y, z). Для каждой величины x, y, z,…мы имеем в результате прямых измерений следующие данные:
где Частная производная функции многих переменных по одной переменной, скажем х, является обычной производной функции по х, причем все остальные переменные y, z,… считаются постоянными параметрами. Относительную ошибку величины Х легко вычислить, написав
Так как то для относительной погрешности получаем:
Порядок обработки результатов при косвенных измерениях 1. Вычислить среднее значение искомой величины по результатам прямых измерений 2. Вычислить относительную погрешность 3. Вычислить абсолютную погрешность косвенных измерений по формуле:
4. Окончательный результат записывается в виде:
ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ 2.1. Подготовка таблиц в лабораторном журнале
Необходимость получения достаточно точного значения измеряемой физической величины требует повторения измерения в одних и тех же условиях. Обычно необходимое число измерений указано в описании к данной лабораторной работе или указывается преподавателем. Однако, во всех случаях необходимо помнить, что с ростом числа измерений возрастает и точность полученного результата. Поэтому в большинстве лабораторных работ физического практикума необходимо проводить 5 – 10 измерений в равных условиях. Исключения допускаются только в том случае, если есть полная уверенность в том, что измеряемая величина имеет, в принципе, точное значение и для ее измерения используют очень точные приборы. Так, в первой лабораторной работе по определению плотности твердого тела масса тела является такой величиной, если для ее определения используют достаточно точный прибор – аналитические весы с погрешностью 0,05 мг. В случае хорошо налаженных аналитических весов массу тела можно было бы определять один раз, но неаккуратное обращение с весами студентов, ранее выполнявшими взвешивание, приводит к тому, что чувствительность весов резко ухудшается, и они уже не являются достаточно точным прибором. Поэтому массу тела необходимо измерять многократно. В первой же лабораторной работе линейные размеры (длину, высоту и ширину) или диаметр и высоту измеряемого тела необходимо измерять многократно, что вызвано как неточностью измерительных приборов, неточностью линейных размеров в разных местах измеряемого тела.
Студент допускается к выполнению лабораторной работы только при наличии у него домашней подготовки, содержащей краткий теоретический анализ экспериментальной задачи, описание лабораторной установки и подготовленные таблицы для записи результатов измерений. Для подготовки такой таблицы студент должен определить количество измеряемых величин и необходимое число измерений. Так, в первой лабораторной работе в случае цилиндрического измеряемого тела количество измеряемых величин равно трем: масса, высота и диаметр цилиндра, а в случае параллелепипеда количество измеряемых величин равно четырем: масса, длина, ширина и высота параллелепипеда. Для каждой величины проводится 5 измерений. Для оформления результатов требуется для каждой величины 3 вертикальных колонки. Таким образом, для цилиндрического тела таблица должна иметь десять колонок в соответствии с примером таблицы (см. таблицу 3).
Записи результатов измерений цилиндрического тела
Таблица 3
В случае, если тело имеет форму параллелепипеда, нужно добавить еще три колонки для третьего линейного размера. При непосредственном выполнении лабораторной работы студент заполняет последовательно колонки для m, H и D. Внизу таблицы студент указывает приборные погрешности dm, dH и dD, определенные, как указано далее.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.011 с.) |







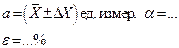
 , причем, х определяется из прямых измерений
, причем, х определяется из прямых измерений  . При изменении х на dх произойдет изменение функции Х на dX. Применяя разложение функции
. При изменении х на dх произойдет изменение функции Х на dX. Применяя разложение функции  в ряд Тейлора:
в ряд Тейлора: ,
,



 Доверительные интервалы D x, D y, D z для прямых измерений находятся методом, указанном в порядке обработки результатов прямых измерений, придерживаясь строгого правила: все доверительные интервалы D x, D y, D z определяются в соответствии с табл. 2 для одного и того же значения доверительной вероятности a. Оценка доверительного интервала D C в этом случае, как это следует из теории [1, 2, 4], производится по формуле:
Доверительные интервалы D x, D y, D z для прямых измерений находятся методом, указанном в порядке обработки результатов прямых измерений, придерживаясь строгого правила: все доверительные интервалы D x, D y, D z определяются в соответствии с табл. 2 для одного и того же значения доверительной вероятности a. Оценка доверительного интервала D C в этом случае, как это следует из теории [1, 2, 4], производится по формуле:
 - частные производные f (x, y, z, …) по переменным x, y, z соответственно, вычисленные для их средних значений.
- частные производные f (x, y, z, …) по переменным x, y, z соответственно, вычисленные для их средних значений.


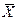 .
. косвенных измерений, учитывая абсолютные погрешности прямых измерений
косвенных измерений, учитывая абсолютные погрешности прямых измерений




