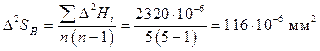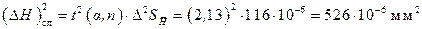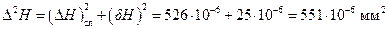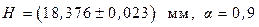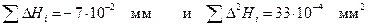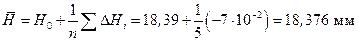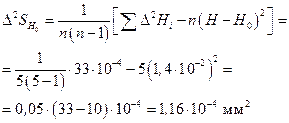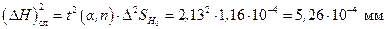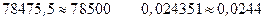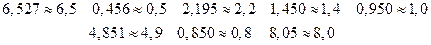Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика расчета погрешностей прямых измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторная работа считается выполненной после заполнения в таблице колонок для измеренных величин и обязательного утверждения этих результатов преподавателем. Рассмотрим теперь порядок оформления результатов на примере расчета высоты цилиндра в лабораторной работе «Определение плотности твёрдого тела». Сразу отметим, что заполнение остальных колонок таблицы и трудоемкость расчетов существенно зависят от того, какой методикой расчетов будет пользоваться студент. Первый вариант основан на использовании при расчетах среднеарифметического значения измеряемой величины, расчет ведется по наиболее коротким формулам, но требует длительных расчетов даже при применении микрокалькуляторов. Второй вариант более прост, все операции производятся с малыми числами и могут быть проделаны без применения микрокалькуляторов, но формулы несколько более сложные.
Вариант 1. Предположим, что в результате измерений были получены значения измерений, занесенные в колонку 2 таблицы 4.
Оформление результатов измерения (расчеты по варианту 1)
Таблица 4
Не заполняя колонки 3 и 4, рассчитываем среднеарифметическое значение величины H:
где Hi – каждое из чисел в колонке 2; n – число измерений.
Для данных таблицы 4:
Затем находим отклонение каждого измерения от среднеарифметического значения с учетом знака:
Эти расчеты нужно занести в колонку 3 таблицы 4. Во избежание большого количества нулей с последующей трудностью их учета, не следует заносить в таблицу результаты в виде промежуточного значения (-0,006), а следует порядок (10-3)
Квадрат погрешности измерений за счет случайного разброса равен (коэффициент Стьюдента выбран из таблицы 2 для a = 0,9 и n = 5 t (a, n) = 2,13)
Тогда квадрат границы доверительного интервала (приборная погрешность определена заранее в соответствии с указаниями, изложенными выше) равен:
Извлекая квадратный корень, окончательно записываем результат в виде:
Обращаем внимание на точность самих расчетов. Количество цифр после запятой в исходных данных - 2. Такое повышение количества значащих цифр оправдано, так как это значение H в дальнейшем будет использовано для расчета плотности. Если бы H было конечной целью работы, то необходимо было оставить столько цифр, сколько было получено в результате измерений – 2 цифры после запятой и записать ответ в виде:
Увеличение сверх трех количества цифр после запятой приводит только к ненужным затратам времени и не дает никакой информации.
Вариант 2. При расчетах по этому варианту таблицу 4 заполняют сразу, не проводя основных расчетов. Для этого выбирают опорную, базовую величину, H 0, не сильно отличающуюся от среднеарифметического значения. Так, для нашего примера такой величиной являлось бы одно из чисел: 18,37 или 18,38 или 18,39. Примем H 0 = 18,39. Тогда D H 1 = 18,37 - 18,39 = -0,02. Эти расчеты выполняют в уме и сразу заполняют таблицы 5 с учетом замечаний о записях результатов, т.е. разность увеличивают в сто раз, а множитель 102 заносят в верхнюю стоку таблицы. Затем заполняют колонку 4, занося множитель 104 в верхнюю стоку таблицы. Находят сумму.
Оформление результатов измерения (расчеты по варианту 2)
Таблица 5
Далее проводят расчеты по формулам:
О приближенных вычислениях
При выполнении вычислений необходимо всегда руководствоваться практически необходимой точностью. Вести вычисления с точностью большей, чем это допускают данные задачи – бессмысленно. Числовые данные бывают двух типов. Одни в точности задают истинную величину, другие – приблизительно. Первые называются точными, вторые – приближенными. Например, батарея конденсаторов состоит из 5 конденсаторов емкостью по 50 пФ. Число 5 – точное, а число 50 пФ – приближенное. Теория приближенных вычислений позволяет: 1. Зная степень точности данных, оценить степень точности результатов еще до выполнения числовых операций;
2. Брать для расчетов данные с надлежащей степенью точности, достаточной, чтобы обеспечить требуемую точность результата, и в то же время не слишком большой, чтобы избавиться от бесполезных вычислений. При записи приближенных чисел следует иметь в виду, что значащими называют все цифры числа, кроме нулей, стоящих впереди числа. Например, в числе 0,00013405 пять значащих цифр; в числе 0,1200 и 5010 – четыре. Число значащих цифр некоторого числа называется его значимостью. В приближенных вычислениях часто приходится округлять числа как приближенные, так и точные, т.е. отбрасывать одну или несколько цифр. Чтобы обеспечить наибольшую близость округленного числа к округляемому, следует соблюдать следующие правила: 1. Если первая из отбрасываемых цифр больше, чем 5, то последняя из сохраняемых цифр увеличивается на единицу. Увеличение совершается и тогда, когда первая из отбрасываемых цифр равна 5, а за ней одна или несколько значащих цифр. Например, округляя приведенные ниже числа до трех значащих цифр, получаем:
2. Если первая из отбрасываемых цифр меньше, чем 5, увеличение не делается. Например, округляя приведенные числа до трех значащих цифр, получим
3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя, сохраняемая цифра остается неизменной, если она четная и увеличивается, если она нечетная. Это связано с тем, что при многочисленных округлениях избыточные числа будут встречаться примерно столь же часто, как и недостаточные. Взаимная компенсация погрешностей обеспечит наибольшую точность результата. Например, округляя числа до первого десятичного знак, получаем:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.011 с.) |

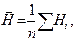
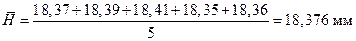
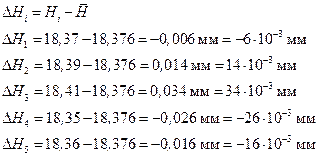
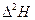 для каждого измерения и
для каждого измерения и 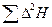 и результаты заносим в колонку 4 таблицы 4. Затем находим квадрат среднеквадратичного отклонения
и результаты заносим в колонку 4 таблицы 4. Затем находим квадрат среднеквадратичного отклонения