
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Гаусса и его основные характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В случае большого числа измерений (
открытому Гауссом. Функция P (X) симметрична относительно а, достигает максимума при Х = а (рис.4). Кроме параметра а функция P (X) задается еще параметром s, который называется стандартным отклонением. Величина D = s 2 называется дисперсией распределения и имеет смысл среднего значения квадрата отклонения Х от истинного значения а, т.е. Р (Х) быстро стремится к нулю, когда Х становится большим по сравнению с s. Функция нормального распределения имеет вид:
Отклонения по обе стороны от центра распределения наблюдаются тем реже, чем больше абсолютная величина таких отклонений. Если изменить метод измерения величины а и измерять ее другим прибором, например, более совершенным, более точным, то разброс результатов измерений будет около центра с прежней абсциссой а, но разброс результатов существенно уменьшится (рис. 5, кривая 1). Если же точность метода измерений ниже, чем для кривой 2, то разброс результатов увеличится и кривая станет более пологой (рис. 5, кривая 3). Трем кривым на рис. 5 соответствуют разные значения стандарта отклонения s, который характеризует размах (разброс) случайных отклонений, присущих данному методу измерения. При этом площадь под кривыми распределения для разных s одна и та же. Параметры а и s в распределении Гаусса, как правило, неизвестны и их нужно искать по данным значениям Х 1, Х 2, … Хn, полученным из опыта. В теории погрешностей существует метод (максимального правдоподобия), который позволяет установить связь между параметрами распределения Гаусса а и s и набором результатов измерений физической величины. Используя этот метод, можно строго математически доказать, что наиболее правдоподобной оценкой истинного значения измеряемой величины является среднее арифметическое из данных измерений, т.е.
а наилучшей оценкой второго параметра s является средняя квадратичная погрешность среднего Расчет осуществляется по формуле:
1.4. Понятие доверительного интервала и доверительной вероятности (надежности)
Среднее арифметическое Однако мы не может достоверно утверждать, что истинное значение а окажется внутри интервала
Расчет показывает, что уже при числе измерений В случае, когда
Распределение Стьюдента
Формула (3), по которой оценивается среднеквадратичное отклонение s, является справедливой лишь при Чтобы получить оценку доверительного интервала для величины а в случае малых n, в теории погрешностей вместо отношения
Эта величина (коэффициент Стьюдента) является функцией числа измерений n и величины a - доверительной вероятности, которая нам задается или же мы ее выбираем сами. Оказывается, что случайная величина при малых n распределена не по нормальному закону (1), а по закону, открытому Стьюдентом. Вид этого закона существенно зависит от выбора n. Плотность вероятности распределения P (t), соответствующая закону Стьюдента, имеет вид:
где
При Задавая надежность a, равную определенной величине, при данном значении n, по табл.2 можно определить коэффициент t. Тогда, определив предварительно
Таблица 2.
Истинное значение измеряемой величины а будет находиться в пределах интервала (
Объективным критерием качества проведенных измерений является относительная погрешность, определяемая отношением абсолютной погрешности к среднему значению измеряемой величины:
Выявление промахов Ранее уже говорилось, что если взять доверительный интервал
1.7. Выбор числа необходимых измерений и учет погрешности измерительного Иногда условия работы требуют получение максимальной точности с использованием определенного измерительного устройства, имеющего цену деления D С. Считается, что экспериментатор достоверно устанавливает значение показаний прибора с точностью
Тогда
Ясно, что в результате измерений нельзя сделать ошибку меньше, чем та, которая определяется погрешностью измерительного прибора. Поэтому в окончательном результате в качестве абсолютной погрешности принимают случайную погрешность только тогда, когда она существенно превышает приборную. В случае, когда эти требования не выполняются и случайная погрешность оказывается сравнимой с приборной погрешностью d, границы доверительного интервала определяются по формуле:
Если же приборная погрешность является определяющей, т.е. ее величина существенно больше величины случайной погрешности, присущей данному методу, то в окончательном результате учитывают только приборную погрешность. В этом случае многократные измерения не выполняют.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

 ), случайный разброс значений измеряемой величины подчиняется закону,
), случайный разброс значений измеряемой величины подчиняется закону, 
 , где
, где  — средний квадрат отклонения измеряемой величины от истинного значения.
— средний квадрат отклонения измеряемой величины от истинного значения. (1)
(1)
 (2)
(2) .
. (3)
(3) является приближенной оценкой истинного значения а измеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо обязательно указать, какова погрешность полученного результата D X. Величину абсолютного отклонения среднего
является приближенной оценкой истинного значения а измеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо обязательно указать, какова погрешность полученного результата D X. Величину абсолютного отклонения среднего  , мы можем сказать лишь следующее: имеется какая-то вероятность того, что а лежит в пределах этого интервала. Следовательно, доверительный интервал D X необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания вероятности a сам по себе интервал D Х не может быть принят в качестве оценки погрешности результата.
, мы можем сказать лишь следующее: имеется какая-то вероятность того, что а лежит в пределах этого интервала. Следовательно, доверительный интервал D X необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания вероятности a сам по себе интервал D Х не может быть принят в качестве оценки погрешности результата. (4)
(4) выбор погрешности
выбор погрешности  , дает величину надежности a, равную 0,68. Другими словами, если взять интервал надежности
, дает величину надежности a, равную 0,68. Другими словами, если взять интервал надежности  , то можно утверждать, что в 68 случаях из 100 истинная величина а попадет в указанный интервал, а в 32 случаях из 100 – не попадет в этот интервал.
, то можно утверждать, что в 68 случаях из 100 истинная величина а попадет в указанный интервал, а в 32 случаях из 100 – не попадет в этот интервал. , то a получается равной 0,95. Если
, то a получается равной 0,95. Если  , a = 0,997, т.е. за пределы доверительного интервала выйдет всего лишь около 3 измерений из 1000.
, a = 0,997, т.е. за пределы доверительного интервала выйдет всего лишь около 3 измерений из 1000. . Число измерений в реальных опытах не может быть бесконечно большим, поэтому использовать среднеквадратичное отклонение для ограниченного числа измерений нельзя.
. Число измерений в реальных опытах не может быть бесконечно большим, поэтому использовать среднеквадратичное отклонение для ограниченного числа измерений нельзя. , вводят величину
, вводят величину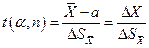 (5)
(5) , (6)
, (6) — гамма-функции.
— гамма-функции. На рис.6 приведены кривые распределения Стьюдента для различных значений n.
На рис.6 приведены кривые распределения Стьюдента для различных значений n. распределение Стьюдента переходит в распределение Гаусса. Распределение Стьюдента позволяет оценить величину погрешности результата D X при заданной доверительной вероятности a, или, наоборот, при заданном D X найти величину a. Действительно, если выбрать на оси t (n, a) некоторое значение t * (рис.6), то вероятность a определяется заштрихованной площадью, причем величина a будет зависеть не только от t, но и от n. Значение коэффициента Стьюдента t для различных значений n и a, рассчитанные в соответствии с законом Стьюдента, приведены в таблице 2.
распределение Стьюдента переходит в распределение Гаусса. Распределение Стьюдента позволяет оценить величину погрешности результата D X при заданной доверительной вероятности a, или, наоборот, при заданном D X найти величину a. Действительно, если выбрать на оси t (n, a) некоторое значение t * (рис.6), то вероятность a определяется заштрихованной площадью, причем величина a будет зависеть не только от t, но и от n. Значение коэффициента Стьюдента t для различных значений n и a, рассчитанные в соответствии с законом Стьюдента, приведены в таблице 2. по формуле (3), можно оценить абсолютную погрешность результата (доверительный интервал) D Х по формуле:
по формуле (3), можно оценить абсолютную погрешность результата (доверительный интервал) D Х по формуле: (7)
(7) ) с вероятностью a, т. е.
) с вероятностью a, т. е.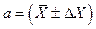 (8)
(8) (9)
(9) , то только в 3 случаях из 1000 измерений можно ожидать выход измерений из указанного доверительного интервала. Если не ставится специальная задача, где точность играет основную роль, то можно считать данные, выходящие за доверительный интервал
, то только в 3 случаях из 1000 измерений можно ожидать выход измерений из указанного доверительного интервала. Если не ставится специальная задача, где точность играет основную роль, то можно считать данные, выходящие за доверительный интервал  , промахами и их при чистовой обработке не учитывать. В практических расчетах, при ограниченном числе измерений, для оценки промахов предполагается, что
, промахами и их при чистовой обработке не учитывать. В практических расчетах, при ограниченном числе измерений, для оценки промахов предполагается, что  .
.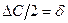 (здесь d - погрешность измерительного прибора). Если задаться доверительной вероятностью a = 0,68, то можно составить равенство для определения числа необходимых измерений n:
(здесь d - погрешность измерительного прибора). Если задаться доверительной вероятностью a = 0,68, то можно составить равенство для определения числа необходимых измерений n:  . Подставляя
. Подставляя 
 (10)
(10) (11)
(11)


