
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие дифференцируемой функцииСодержание книги
Поиск на нашем сайте
ОПРЕДЕЛЕНИЕ 5. Функция где Заметим, что функция ОПРЕДЕЛЕНИЕ 6. Линейная функция (относительно Замечание. Заметим, что дифференциал функции является линейной функцией, зависящей от Кроме того, дифференциал является главной частью приращения функции, то есть щджз Более того, приращение функции в точке
ТЕОРЕМА 1. Для того, чтобы функция
Доказательство. Необходимость. Пусть функция дифференцируема в точке Тогда По определению это означает, что существует производная Достаточность. Пусть существует производная
Так как Замечание. Из равенства (6) следует, что Мы получаем еще одно обозначение производной.
ОПРЕДЕЛЕНИЕ 7. Приращение независимой переменной СЛЕДСТВИЕ. Если функция
ТЕОРЕМА 2. Если функция Доказательство. Пусть функция По определению это означает, что функция непрерывна в точке
Обратное утверждение неверно. Непрерывность функции в точке не гарантирует дифференцируемость функции в точке. ПРИМЕР 1. Функция непрерывна в точке Однако ПРИМЕР 2. Функция непрерывна в точке
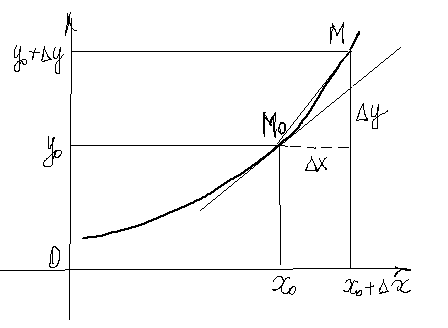
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА Понятие производной связано с понятием касательной. Определим понятие касательной к графику функции в точке
Пусть функция Проведем секущую где Покажем, что при В силу непрерывности функции ОПРЕДЕЛЕНИЕ. Если существует ОПРЕДЕЛЕНИЕ. Если и перейдем к пределу при
Существование конечного предела Если Известно, что
Так как
Если в точке Если в точке
В таких случаях точка
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.006 с.) |

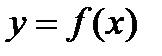 , определенная в окрестности точки
, определенная в окрестности точки 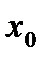 , называется дифференцируемой в точке
, называется дифференцируемой в точке 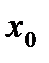 , если существует число
, если существует число 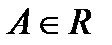 такое, что приращение функции в точке может быть записано в виде
такое, что приращение функции в точке может быть записано в виде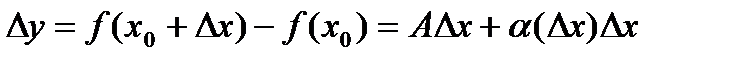 , (2)
, (2)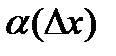 - бесконечно малая функция при
- бесконечно малая функция при 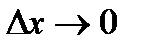 .
.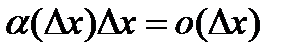 , и равенство (2) может быть переписано в виде
, и равенство (2) может быть переписано в виде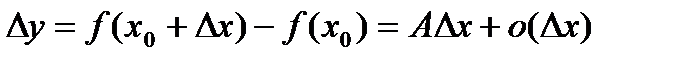 при
при 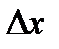 )
) 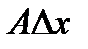 называется дифференциалом функции
называется дифференциалом функции 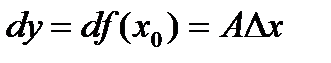 (4)
(4) .
.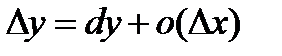 при
при 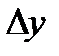 и дифференциал функции в точке
и дифференциал функции в точке 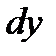 являются эквивалентными бесконечно малыми функциями при
являются эквивалентными бесконечно малыми функциями при 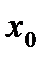 , необходимо и достаточно, чтобы функция имела производную в этой точке
, необходимо и достаточно, чтобы функция имела производную в этой точке 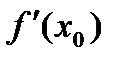 , при этом
, при этом 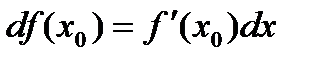 .
. 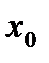 , тогда, по определению,
, тогда, по определению, 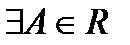 такая, что
такая, что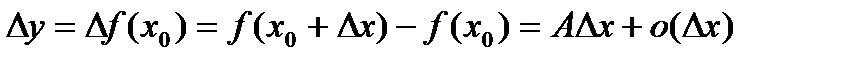 при
при 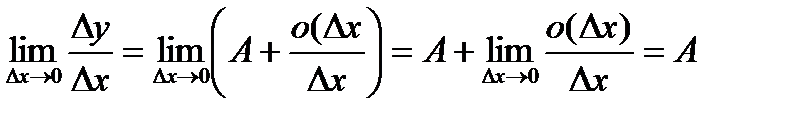 .
.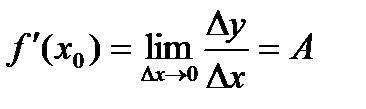 , и дифференциал функции в точке
, и дифференциал функции в точке  . (6)
. (6)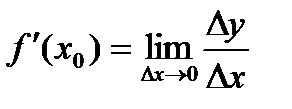 . Тогда
. Тогда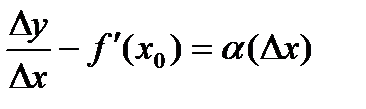 , причем
, причем 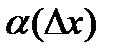 - бесконечно малая функция при
- бесконечно малая функция при 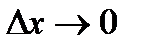 . Отсюда получаем
. Отсюда получаем 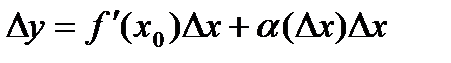 .
. при
при 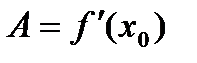 .
.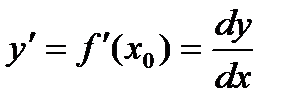 .
.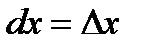 .
.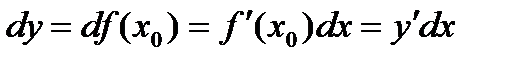 . (7)
. (7)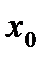 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.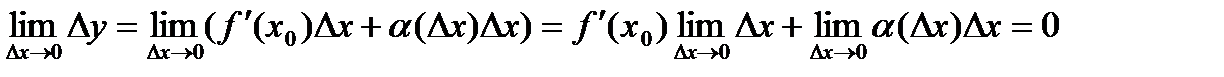 .
.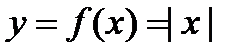 .
.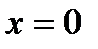 , так как
, так как  ,
, 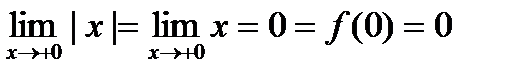 , функция непрерывна слева и непрерывна справа.
, функция непрерывна слева и непрерывна справа.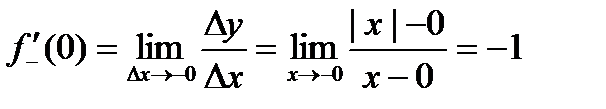 ,
, 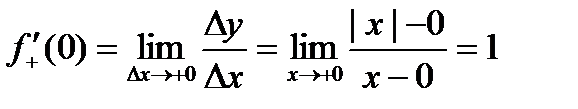 , то есть односторонние производные не равны, следовательно производная в точке
, то есть односторонние производные не равны, следовательно производная в точке 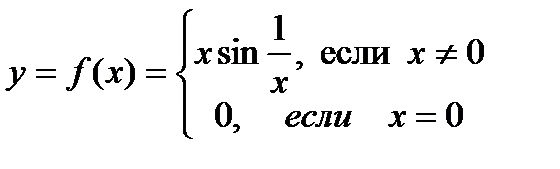 .
.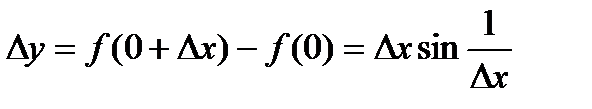 , справедливо неравенство
, справедливо неравенство 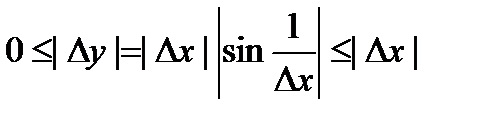 ,
, 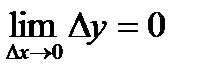 .
.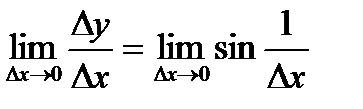 не существует, то есть не существует производная функции в точке
не существует, то есть не существует производная функции в точке 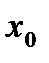 .
.
 определена на интервале
определена на интервале 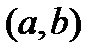 и непрерывна в точке
и непрерывна в точке 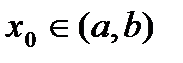 ,
, 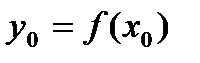 ,
, 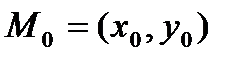 . Пусть
. Пусть 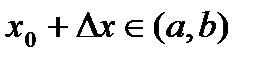 ,
, 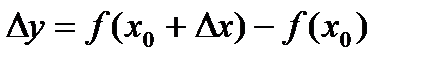 ,
, 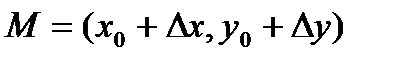 .
.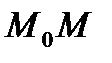 . Секущая имеет уравнение
. Секущая имеет уравнение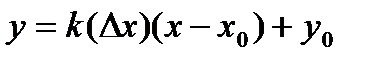 , (8)
, (8)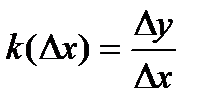 .
.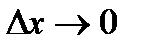 длина отрезка
длина отрезка 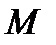 стремится к точке
стремится к точке 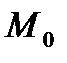 .
.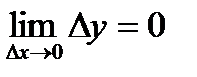 , тогда
, тогда 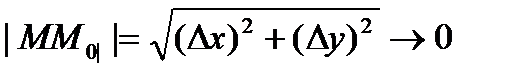 .
.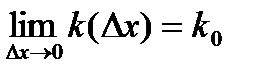 , то прямая, уравнение которой
, то прямая, уравнение которой 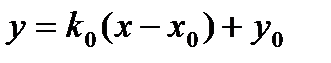 получается и уравнения секущей
получается и уравнения секущей 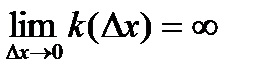 , то прямая
, то прямая 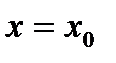 , которая получается из уравнения секущей (8), если мы поделим обе части равенства (8) на
, которая получается из уравнения секущей (8), если мы поделим обе части равенства (8) на 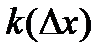
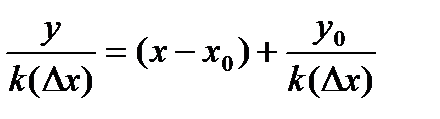
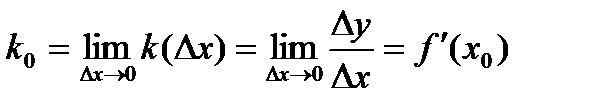 . То есть, если функция
. То есть, если функция 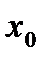 , то уравнение касательной к графику функции имеет вид
, то уравнение касательной к графику функции имеет вид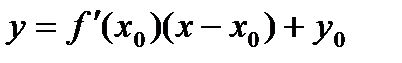 , где
, где 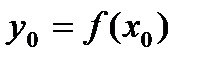 .
.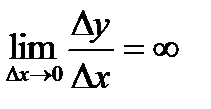 , то уравнение касательной
, то уравнение касательной 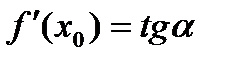 , тангенс угла между касательной к графику функции в точке
, тангенс угла между касательной к графику функции в точке 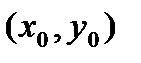 и осью
и осью 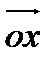 .
.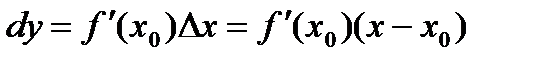 , с другой стороны на касательной
, с другой стороны на касательной 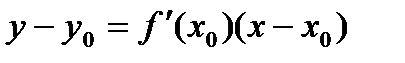 , получаем, что дифференциал функции в точке равен приращению линейной функции, задающей касательную к графику функции.
, получаем, что дифференциал функции в точке равен приращению линейной функции, задающей касательную к графику функции.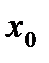
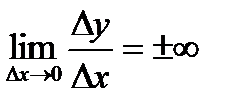 (то есть
(то есть 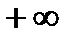 или
или 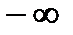 ) будем говорить, что существует бесконечная производная (
) будем говорить, что существует бесконечная производная (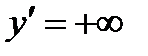 или
или 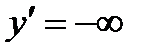 ).
).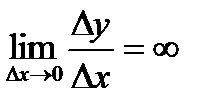 , но не равен
, но не равен 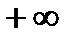 или
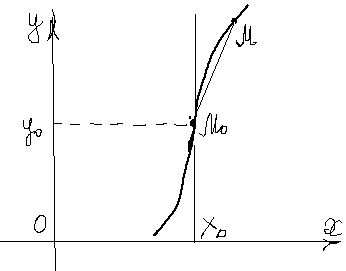
или 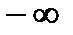 , то график функции имеет следующий вид
, то график функции имеет следующий вид 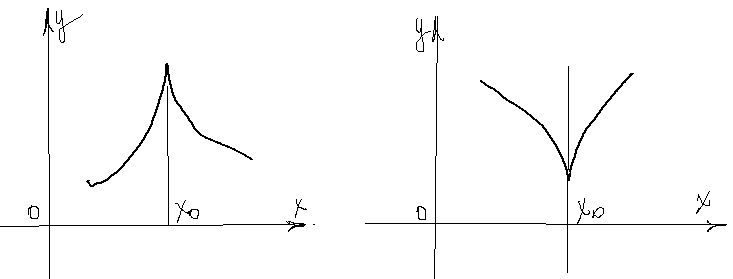
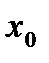 называется точкой возврата.
называется точкой возврата.


