
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметические операции над непрерывными функциями
1. Если функция В самом деле, 2. Если функции В самом деле, 3. Если функции В самом деле, 4. Если функции В самом деле,
ПРИМЕР 1. Функция
Пусть ПРИМЕР 2. Функция Составим приращение функции
Последнее означает, что функция непрерывна в любой точке ПРИМЕР 3. Исследовать на непрерывность функцию
Непрерывность элементарных функций.
1.
2. По определению, 3.
ЛЕММА.
Пусть
Пусть Пусть
4. Составим приращение функции
5. Составим приращение функции
6. Эта функция непрерывна во всех точках, кроме тех, в которых 7. Эта функция непрерывна во всех точках, кроме тех, в которых
Первый замечательный предел
Пусть
Следствие 1. Доказательство. Следствие 2. Литература. 2. Кудрявцев Л.Д. Математический анализ, т.1, §§ 5,6. 3. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, т 1, глава вторая, § 4.
КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА
Вспомним определение непрерывной в точке функции. ОПРЕДЕЛЕНИЕ 1. Пусть функция То есть для непрерывности функции 1. Функция должна быть определена в окрестности точки 2. Должен существовать предел функции в этой точке 3. Предел функции в точке должен быть равен значению функции в этой точке, то есть должно выполняться равенство (1).
ОПРЕДЕЛЕНИЕ 2. Пусть функция 1. Функция не определена в точке 2. Не существует предел функции в точке 3. Предел существует, функция определена в точке, но не выполняется равенство (1).
ОПРЕДЕЛЕНИЕ 3. Точка
ПРИМЕР 1.
Функция не определена в точке Замечание. В устранимой точке разрыва функцию можно доопределить, как в примере, если она не была определена в точке, или изменить значение функции в этой точке, положив значение функции равной пределу. При этом функция станет непрерывной в точке. ОПРЕДЕЛЕНИЕ 4. Точка
Функция ПРИМЕР 2.
ОПРЕДЕЛЕНИЕ 5. Точка
ПРИМЕР 3.
Функция не определена в точке
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.026 с.) |
 непрерывна в точке
непрерывна в точке  , тогда для любой константы
, тогда для любой константы 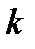 функция
функция 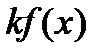 непрерывна в точке
непрерывна в точке 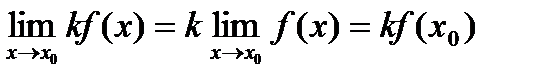 .
.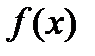 и
и 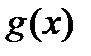 непрерывны в точке
непрерывны в точке 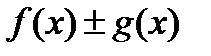 непрерывна в точке
непрерывна в точке 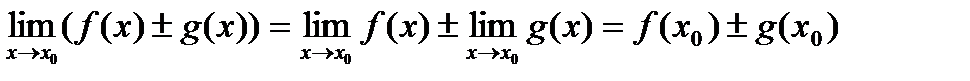 .
.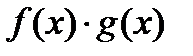 непрерывна в точке
непрерывна в точке  .
.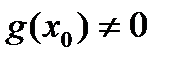 , тогда функция
, тогда функция 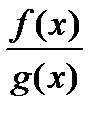 непрерывна в точке
непрерывна в точке 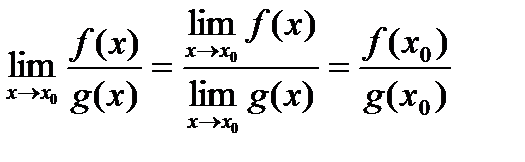 .
.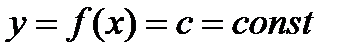 непрерывна в любой точке.
непрерывна в любой точке. - произвольная точка на числовой оси. Составим приращение функции
- произвольная точка на числовой оси. Составим приращение функции 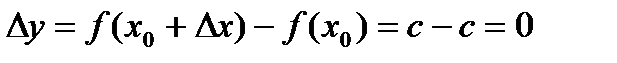 .
. 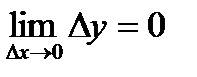 . По определению функция непрерывна в этой точке.
. По определению функция непрерывна в этой точке.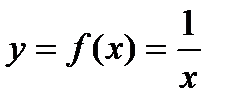 . Исследуем на непрерывность функцию в любой точке
. Исследуем на непрерывность функцию в любой точке  .
.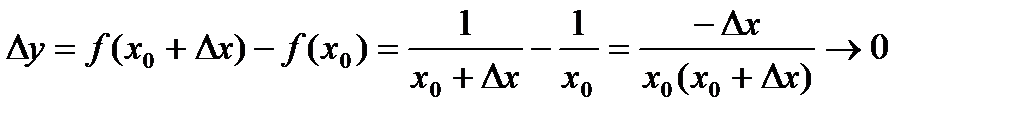 при
при 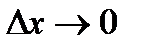 .
.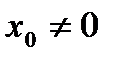 .
.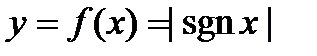 в точке
в точке 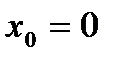 .
. 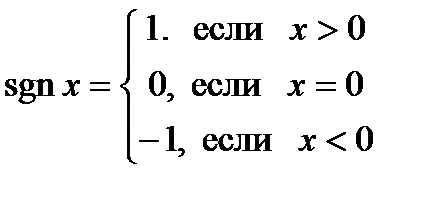 ,
,  .
. ,
, 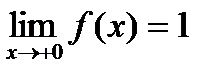 , следовательно, существует предел функции
, следовательно, существует предел функции 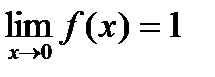 , однако он не равен значению функции
, однако он не равен значению функции  . Функция не является непрерывной в точке
. Функция не является непрерывной в точке 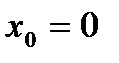 .
.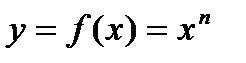 ,
, 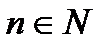 .
.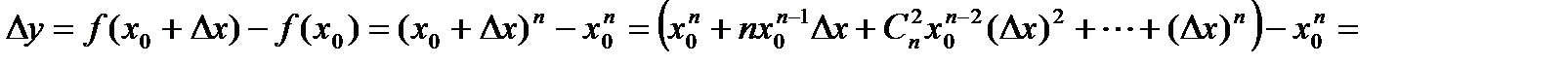
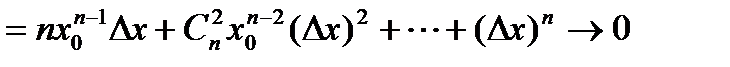 при
при 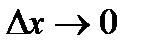 . То есть функция непрерывна в любой точке
. То есть функция непрерывна в любой точке 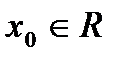 .
. ,
, 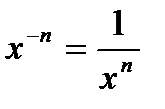 . По свойству непрерывности частного двух функций такая функция непрерывна в любой точке
. По свойству непрерывности частного двух функций такая функция непрерывна в любой точке 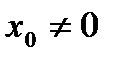 .
.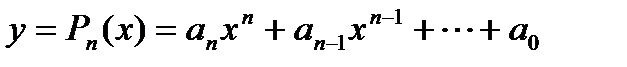 . Такая функция непрерывна в силу свойств непрерывных функций в любой точке
. Такая функция непрерывна в силу свойств непрерывных функций в любой точке 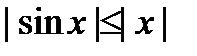 .
.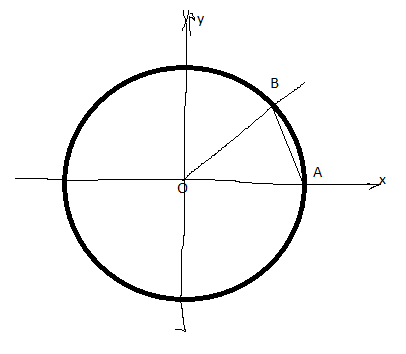
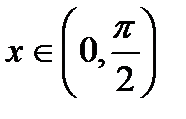 . Найдем площади
. Найдем площади 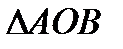 и площадь кругового сектора
и площадь кругового сектора  .
.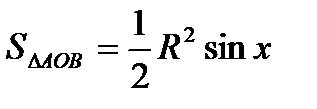 ,
,  .
. 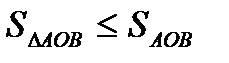 , получаем
, получаем 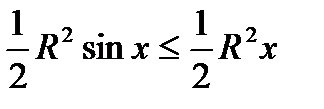 . Отсюда получаем верное неравенство
. Отсюда получаем верное неравенство 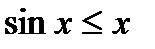 .
.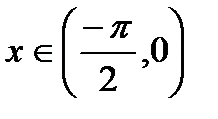 , тогда верно неравенство
, тогда верно неравенство  , то есть верно неравенство
, то есть верно неравенство 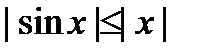 .
.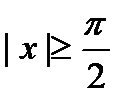 , тогда
, тогда 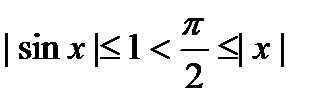 . Неравенство доказано.
. Неравенство доказано.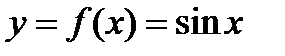 .
.
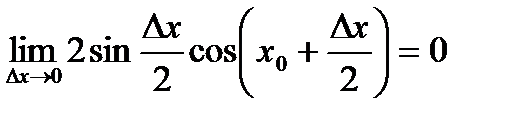 , так как первый множитель бесконечно малый, а второй является ограниченной функцией. По определению функция непрерывная в любой точке
, так как первый множитель бесконечно малый, а второй является ограниченной функцией. По определению функция непрерывная в любой точке  .
.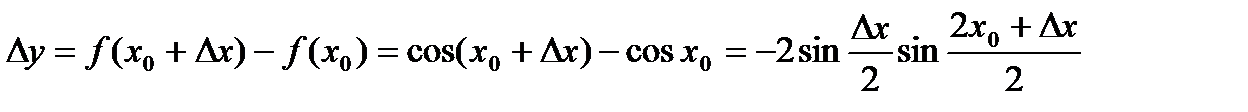
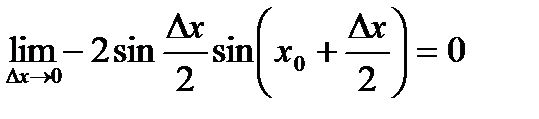 , так как первый множитель бесконечно малый, а второй является ограниченной функцией. По определению функция непрерывная в любой точке
, так как первый множитель бесконечно малый, а второй является ограниченной функцией. По определению функция непрерывная в любой точке 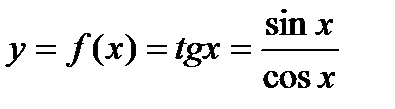 .
.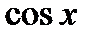 обращается в ноль, то есть при
обращается в ноль, то есть при 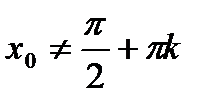 ,
, 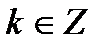 .
. .
.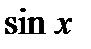 обращается в ноль, то есть при
обращается в ноль, то есть при 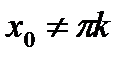 ,
, 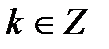 .
.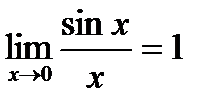

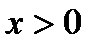
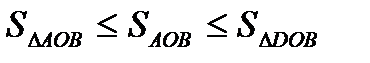 ,
, 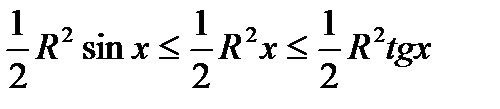 . Отсюда получаем
. Отсюда получаем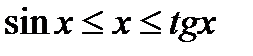 . То есть верно неравенство
. То есть верно неравенство 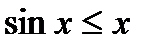 и
и 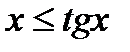 , или
, или 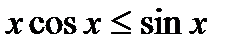 . Получаем
. Получаем  . Делим неравенство на
. Делим неравенство на 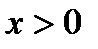 , получаем
, получаем 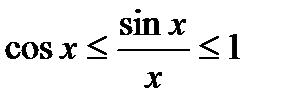 .
. , по теореме о трех пределах имеем
, по теореме о трех пределах имеем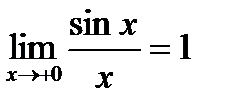 .
. 
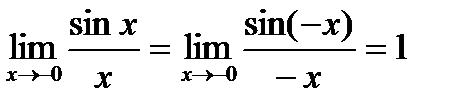 .
. 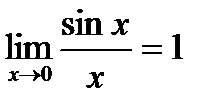
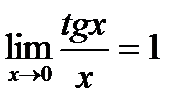 .
.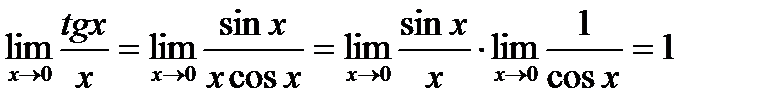 .
. ̴
̴  ,
, 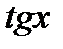 ̴
̴ 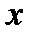 , при
, при 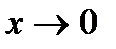 .
.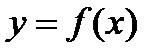 определена в окрестности точки
определена в окрестности точки 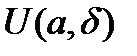 , существует предел функции
, существует предел функции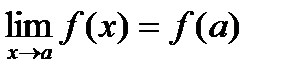 . (1)
. (1) в точке
в точке 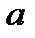 должны выполняться три условия
должны выполняться три условия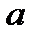 ,
, определена в проколотой окрестности точки
определена в проколотой окрестности точки 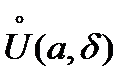 , точка
, точка 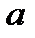 называется точкой разрыва функции
называется точкой разрыва функции  , если выполняется хотя бы одно из условий
, если выполняется хотя бы одно из условий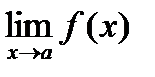 ,
,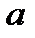 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 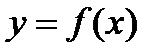 , если существует предел функции в точке
, если существует предел функции в точке 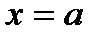 функция или не определена, или она принимает значение
функция или не определена, или она принимает значение  .
.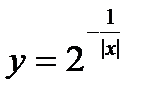
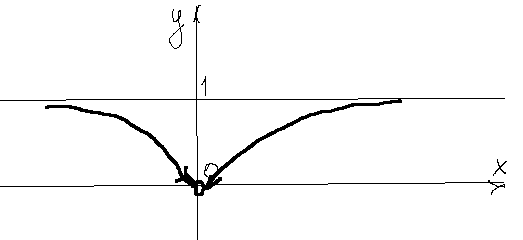
 . Однако существует предел функции в точке
. Однако существует предел функции в точке 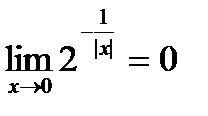 . Если функцию определить в точке
. Если функцию определить в точке  , положив
, положив 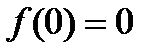 , то функция станет непрерывной в точке
, то функция станет непрерывной в точке 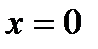 .
.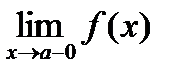 ,
,  , при этом
, при этом  .
.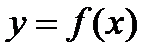 в точке
в точке 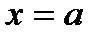 делает конечный скачек
делает конечный скачек 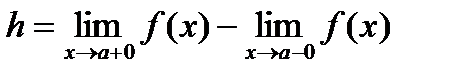 .
.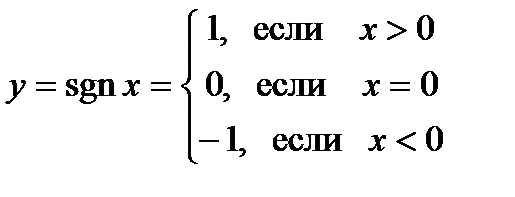

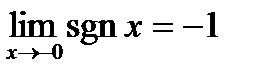 ,
,  , оба односторонних предела конечны, функция в точке
, оба односторонних предела конечны, функция в точке  делает скачек
делает скачек 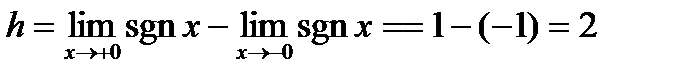 . Функция в точке
. Функция в точке 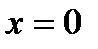 определена,
определена, 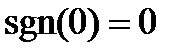 , но она не является непрерывной ни слева, ни справа в этой точке. Точка
, но она не является непрерывной ни слева, ни справа в этой точке. Точка 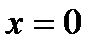 - точка разрыва первого рода
- точка разрыва первого рода .
.
 , но определена во всех остальных точках.
, но определена во всех остальных точках. 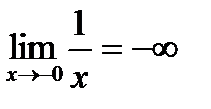 ,
, 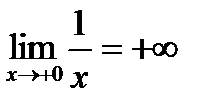 . Оба односторонние пределы бесконечны. Точка
. Оба односторонние пределы бесконечны. Точка 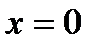 - точка разрыва второго рода.
- точка разрыва второго рода.


