
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы дифференциального исчисления
ТЕОРЕМА (ФЕРМА). Пусть функция Доказательство. По условию теоремы Тогда справедливы неравенства Если существует производная в точке Переходя к пределу в неравенствах (3) при Из последних двух неравенств получаем, что
Геометрическая интерпретация теоремы Ферма. Геометрическая интерпретация теоремы Ферма состоит в том, что, если в точке
ЗАМЕЧАНИЕ. Если функция в точке ПРИМЕР.
ТЕОРЕМА (РОЛЛЯ). Пусть функция Доказательство. Так как функция Если Если
Геометрический смысл теоремы заключается в том, что, если функция непрерывна на на отрезке
Посмотрим, насколько важны все условия теоремы. 1. Если функция не является непрерывной на отрезке, то утверждение неверно
ПРИМЕР.
Функция непрерывна на полуинтервале Делаем вывод, что требование непрерывности функции на отрезке обязательное. 2. Требование существования производной во всех внутренних точках тоже существенное.
ПРИМЕР.
В данном примере функция непрерывна на отрезке
ТЕОРЕМА (ЛАГРАНЖА). Пусть функция Замечание. Последнее равенство называется формулой конечных приращений Лагранжа и может быть записано в виде Доказательство. Введем вспомогательную функцию Число То есть Для функции
Геометрический смысл теоремы состоит в том, что
Приведем другие формы записи формулы Лаграржа. Точка Если мы положим Сравним формулу (6) с приближенной формулой
СЛЕДСТВИЕ 1. Пусть функция Доказательство. Для
Так как
СЛЕДСТВИЕ 2. Пусть функция Доказательство. Пусть Если Если Точка и В силу теоремы о трех пределах Применяя теорему о замене переменных в пределах, получаем Переходя к пределу при
Следовательно, существует предел СЛЕДСТВИЕ 3. Пусть функция Доказательство. По определению функция По формуле конечных приращений Лагранжа имеем
Ограниченность производной означает, по определению, что
Таким образом,
ПРАВИЛО ЛОПИТАЛЯ
Под правилом Лопиталя понимается серия теорем, которые позволяют раскрывать неопределенности типа « ТЕОРЕМА (КОШИ). Пусть функции Доказательство. Заметим, что левая и правая части равенства имеют смысл, так как Рассмотрим вспомогательную функцию Число Функция ТЕОРЕМА 1. Пусть функции Доказательство. Применяя метод выделения главной части, получаем
ТЕОРЕМА 2. Пусть функции
Доказательство. Функции Пусть причем
Теорема доказана. Аналогичные теоремы справедливы для случая
ТЕОРЕМА 3. Пусть функции Доказательство. При вычислении предела сделаем замену переменных
Теорема доказана.
Аналогичная теорема справедлива при
ТЕОРЕМА 4. Пусть функции (без доказательства).
Раскрытие неопределенностей типа « Раскрыть такого типа неопределенности можно, предварительно прологарифмировав соответствующую функцию. ПРИМЕР.
ФОРМУЛА ТЕЙЛОРА
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.081 с.) |
 определена в некоторой окрестности точки
определена в некоторой окрестности точки  и принимает в этой точке наибольшее (или наименьшее) значение. Тогда, если в точке
и принимает в этой точке наибольшее (или наименьшее) значение. Тогда, если в точке  , то
, то 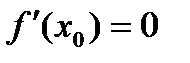 .
.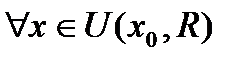
 .
. , если
, если  , и (3)
, и (3)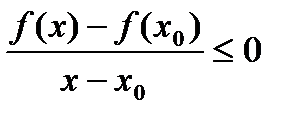 , если
, если 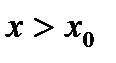 . (4)
. (4) , то существуют и односторонние производные
, то существуют и односторонние производные 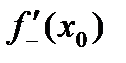 и
и  и они равны
и они равны  .
.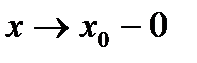 и в (4) при
и в (4) при  , получаем
, получаем ,
, .
.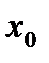 функция принимает наибольшее (наименьшее) значение в некоторой окрестности точки
функция принимает наибольшее (наименьшее) значение в некоторой окрестности точки 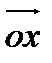
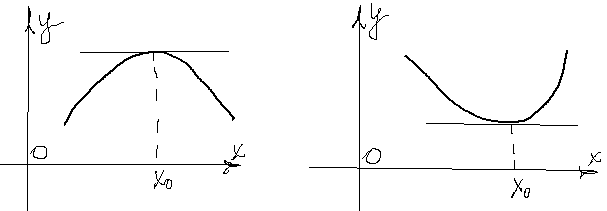

 на отрезке
на отрезке  .
. ,
, 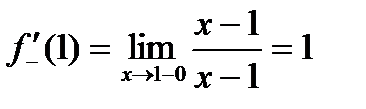 .
.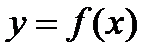 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  ,
, 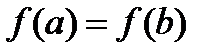 . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка  такая, что
такая, что 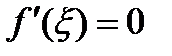 .
.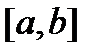 , то по теореме Вейерштрасса она достигает минимального и максимального значений в некоторых точках отрезка. Пусть
, то по теореме Вейерштрасса она достигает минимального и максимального значений в некоторых точках отрезка. Пусть 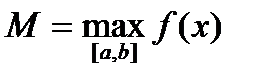 ,
,  ,
, 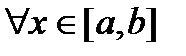 справедливо неравенство
справедливо неравенство 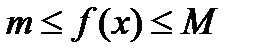 .
.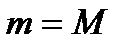 , то
, то 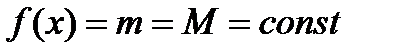 , тогда
, тогда 
 .
.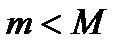 , то хотя бы одно из значений
, то хотя бы одно из значений  или
или 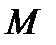 принимается не на концах. Пусть, например
принимается не на концах. Пусть, например 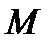 . Тогда существует точка
. Тогда существует точка  такая, что
такая, что  , и в этой точке существует производная
, и в этой точке существует производная 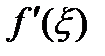 . По теореме Ферма
. По теореме Ферма 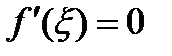 . Теорема доказана.
. Теорема доказана.
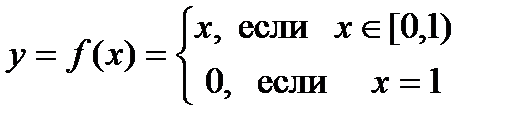 .
.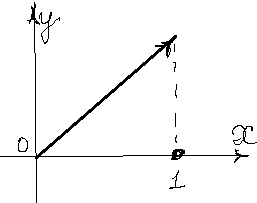
 , на интервале
, на интервале 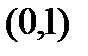 дифференцируема, принимает равные значения на концах отрезка
дифференцируема, принимает равные значения на концах отрезка  . Как видим, производная во всех точках интервала
. Как видим, производная во всех точках интервала  .
. ,
,  .
.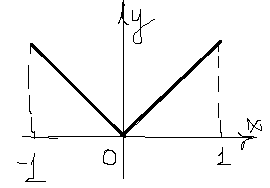
 , принимает на концах отрезка равные значения
, принимает на концах отрезка равные значения 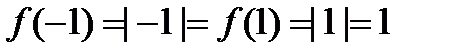 . Однако ни в одной точке производная не обращается в нуль, так как не выполняется условие дифференцируемости функции во всех внутренних точках, в точке
. Однако ни в одной точке производная не обращается в нуль, так как не выполняется условие дифференцируемости функции во всех внутренних точках, в точке 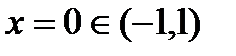 производная не существует.
производная не существует.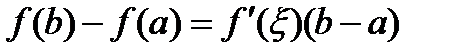 .
.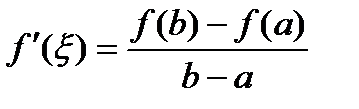 .
. .
. определим из условия
определим из условия  , то есть из равенства
, то есть из равенства  .
. .
.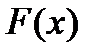 выполняются все условия теоремы Ролля, то есть функция непрерывна на отрезке
выполняются все условия теоремы Ролля, то есть функция непрерывна на отрезке 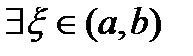 такая, что
такая, что 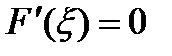 .
.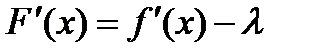 ,
, 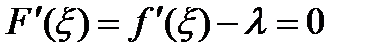 . Тогда
. Тогда . Теорема доказана.
. Теорема доказана.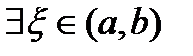 , касательная в которой параллельна хорде, соединяющей точки
, касательная в которой параллельна хорде, соединяющей точки  и
и 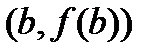 .
.
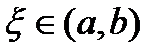 , то есть справедливо неравенство
, то есть справедливо неравенство 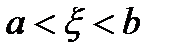 . Обозначим
. Обозначим  . Очевидно
. Очевидно  , тогда
, тогда 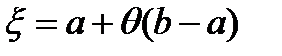 , и формула конечных приращений Лагранжа приобретает вид
, и формула конечных приращений Лагранжа приобретает вид ,
, 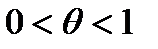 . (5)
. (5) ,
, 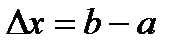 , тогда формула конечных приращений Лагранжа приобретает вид
, тогда формула конечных приращений Лагранжа приобретает вид ,
, 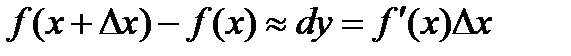 . (7)
. (7) во всех точках интервала
во всех точках интервала  на отрезке
на отрезке  ,
,  имеем
имеем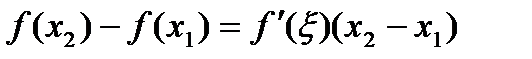 ,
, 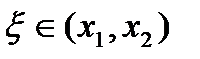 .
. , то
, то 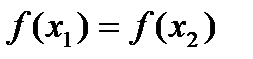
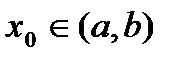 , и существует предел
, и существует предел 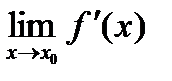 , тогда существует производная
, тогда существует производная 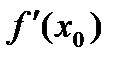 и
и  .
.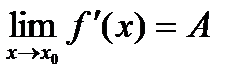 .
. , то
, то 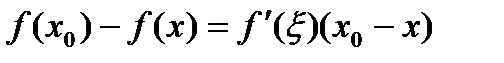 ,
,  , тогда
, тогда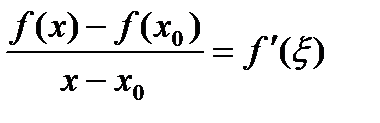 . (8)
. (8) 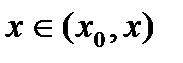 , то
, то  ,
, 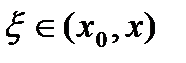 , и справедливо равенство
, и справедливо равенство 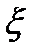 определяется неоднозначно, она зависит от точки
определяется неоднозначно, она зависит от точки 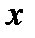 , то есть
, то есть  , причем справедливо неравенство
, причем справедливо неравенство , если
, если  ,
,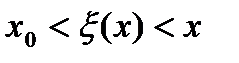 , если
, если 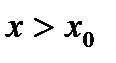 .
. .
.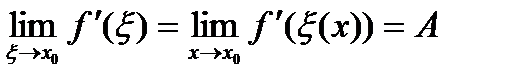 .
.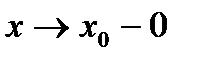 в равенстве (8) и при
в равенстве (8) и при  в равенстве (9), получаем
в равенстве (9), получаем ,
,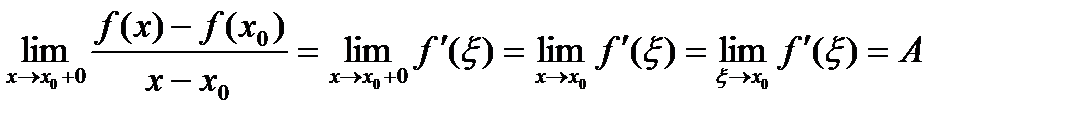 .
.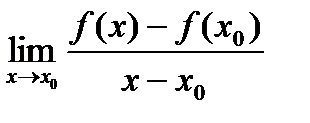 . Последнее по определению означает, что существует производная
. Последнее по определению означает, что существует производная  .
. дифференцируема на промежутке
дифференцируема на промежутке  , и производная функции
, и производная функции  ограничена на этом промежутке, тогда функция
ограничена на этом промежутке, тогда функция  .
.
 , что
, что 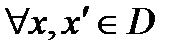 :
: 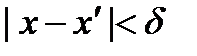 выполняется неравенство
выполняется неравенство 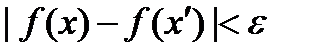 .
.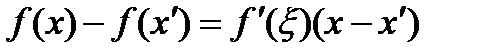 .
.
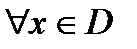
 . Тогда получаем
. Тогда получаем  .
. , что
, что  доказана.
доказана.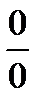 » или «
» или «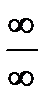 ».
».
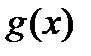 непрерывны на отрезке
непрерывны на отрезке 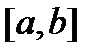 , дифференцируемы на интервале
, дифференцируемы на интервале  и
и 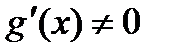
 . Тогда существует точка
. Тогда существует точка  такая, что
такая, что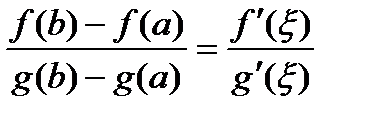 .
.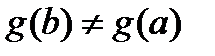 (в противном случае, по теореме Ролля, нашлась бы точка
(в противном случае, по теореме Ролля, нашлась бы точка  , в которой
, в которой  ).
). .
. подберем так, чтобы выполнялось равенство
подберем так, чтобы выполнялось равенство 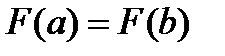 , то есть
, то есть  . Отсюда получаем
. Отсюда получаем  .
.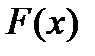 удовлетворяет всем условиям теоремы Ролля, поэтому существует точка
удовлетворяет всем условиям теоремы Ролля, поэтому существует точка 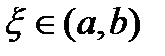 такая, что
такая, что  . То есть
. То есть 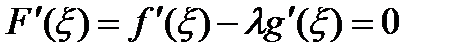 . Отсюда получаем
. Отсюда получаем 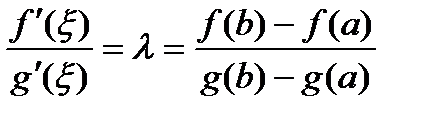 . Теорема доказана.
. Теорема доказана.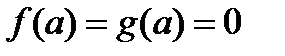 , существуют односторонние производные
, существуют односторонние производные 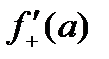 и
и  , причем
, причем 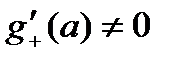 . Тогда существует
. Тогда существует  .
. ,
, 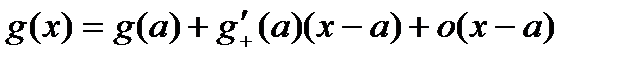 . Так как
. Так как 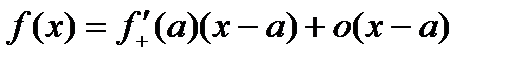 ,
,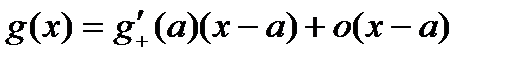 .
.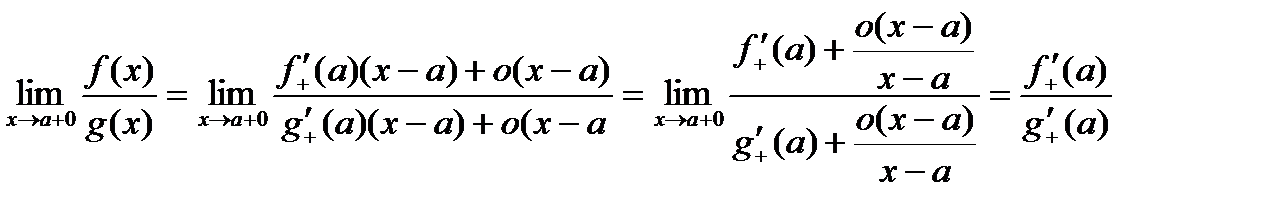 .
. ,
, 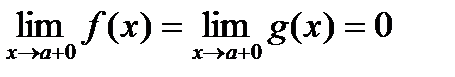 , производная
, производная 
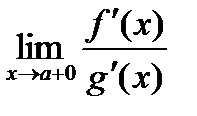 конечный или равный
конечный или равный  ,
,  . Тогда существует
. Тогда существует  .
.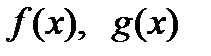 не определены в точке
не определены в точке  , доопределим их, положив
, доопределим их, положив  , тогда функции
, тогда функции 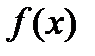 и
и 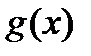 становятся непрерывными на полуинтервале
становятся непрерывными на полуинтервале 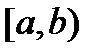 .
.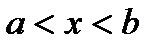 , тогда на отрезке
, тогда на отрезке  функции удовлетворяют условиям теоремы Коши. Тогда
функции удовлетворяют условиям теоремы Коши. Тогда 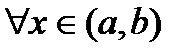
 такая точка, что справедливо равенство
такая точка, что справедливо равенство ,
, . Отсюда следует,
. Отсюда следует,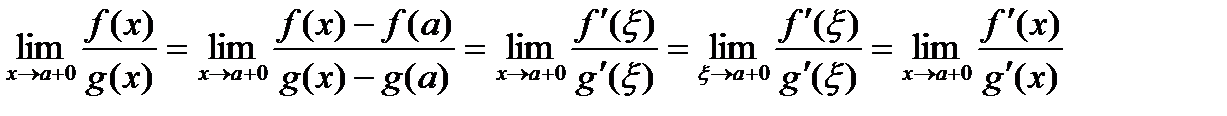 .
. и
и  .
.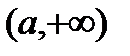 ,
,  , производная
, производная 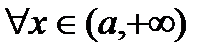 , и существует предел
, и существует предел  конечный или равный
конечный или равный  .
.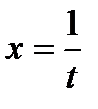 ,
,  и применяем теорему 2.
и применяем теорему 2. .
. .
.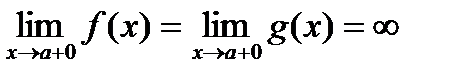 , производная
, производная 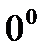 », «
», « » и «
» и «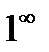 »
» .
. . Следовательно
. Следовательно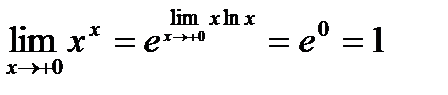 .
.


