
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глобальный экстремум функции
Пусть функция непрерывна на отрезке Максимум может достигаться во внутренней точке, и в этом случае эта точка является одной из точек локального максимума, или в одной из граничных точек. Для нахождения максимального значения функции на отрезке необходимо сравнить значения в точках локального максимума со значениями функции на концах отрезка. Наибольшее из этих значений будет максимальным значением функции на отрезке. Аналогично, минимум достигается или в одной из точек локального минимума, или на границе отрезка. Минимум функции на отрезке находится как минимальное значение функции в точках локального минимума и значений функции на концах отрезка. ПРИМЕР. Найти максимальное и минимальное значение функции Находим точки подозрительные на локальный экстремум
По теореме 1 точка
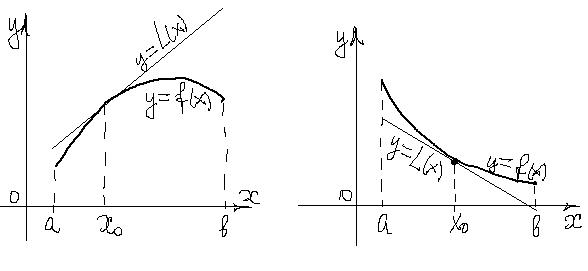
ВЫПУКЛОСТЬ ФУНКЦИИ Пусть функция ОПРЕДЕЛЕНИЕ. Функция
Геометрически выпуклость вверх (вниз) означает, что любая точка хорды
ОПРЕДЕЛЕНИЕ. Функция
ОПРЕДЕЛЕНИЕ. Интервал, на котором функция выпукла (строго или нестрого) вверх или вниз называется интервалом (строгой или нестрогой) выпуклости вверх или вниз соответственно этой функции. ТЕОРЕМА 1. Пусть функция ЛЕММА. Условие выпуклости вверх
а условие выпуклости вниз
Доказательство леммы. Пусть функция
Приведем подобные относительно Умножим левую часть неравенства на Умножаем обе части неравенства на Лемма доказана для случая выпуклой вверх функции, для функции выпуклой вниз доказательство аналогично (будут выполняться противоположные неравенства).
Доказательство теоремы. Необходимость. Пусть функция В неравенстве (7) перейдем к пределу при переходя в неравенстве (7) к пределу при Из неравенств (8) и (9) следует, что Достаточность. Пусть производная
где Последнее неравенство означает в силу леммы, что функция выпукла вверх.
ТЕОРЕМА 1.1. Если функция Доказательство теоремы повторяет доказательство достаточности теоремы 1. В неравенстве (8), так как верное
ТЕОРЕМА 2. Пусть функция
Доказательство. Необходимым и достаточным условием монотонного убывания (возрастания) функции ТЕОРЕМА 3.. Пусть функция
Доказательство. Пусть точка Необходимость. Пусть функция
так как в случае Неравенство (9) означает, что график функции Аналогично доказывается необходимость в случае, если функция выпукла вниз (получаются противоположные неравенства). Достаточность. Пусть Пусть точки Отсюда следует, что неравенство верно
ТОЧКИ ПЕРЕГИБА ОПРЕДЕЛЕНИЕ. Пусть функция Итак, в силу определения,
ПРИМЕР.
И Точка
ТЕОРЕМА 1 (необходимое условие точки перегиба). Пусть функция Доказательство от противного. Пусть
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 99; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.232 (0.026 с.) |
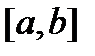 , по теореме Вейерштрасса функция достигает на отрезке
, по теореме Вейерштрасса функция достигает на отрезке  своего максимума и минимума.
своего максимума и минимума. на отрезке
на отрезке  .
. ,
,  при
при 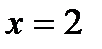 ,
, 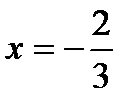 .
.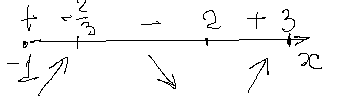
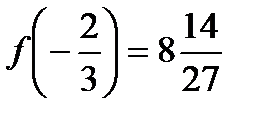 ,
, 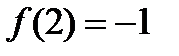 . На концах отрезка функция принимает значения
. На концах отрезка функция принимает значения 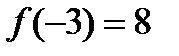 ,
, 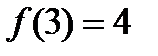 . Максимальное значение функции на отрезке
. Максимальное значение функции на отрезке 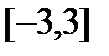 равно
равно 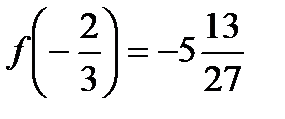 , минимальное
, минимальное 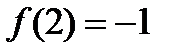 .
. определена на интервале
определена на интервале  , и
, и 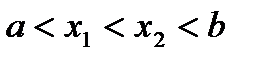 . Проведем через точки
. Проведем через точки  и
и 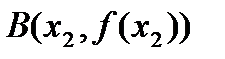 прямую
прямую  ,
, 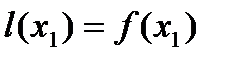 ,
, 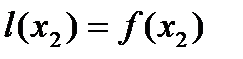 .
. таких, что
таких, что  и
и 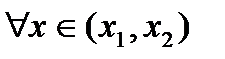 справедливо неравенство
справедливо неравенство 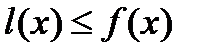 (
( ).
). лежит не выше (не ниже) кривой
лежит не выше (не ниже) кривой 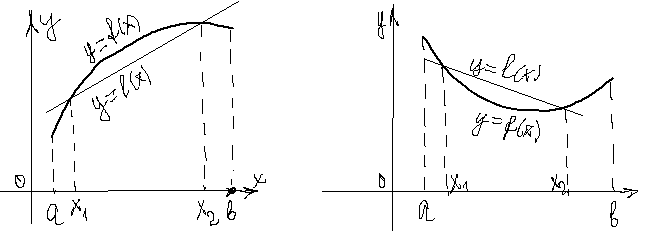
 справедливо неравенство
справедливо неравенство (
(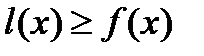 ). (4)
). (4) монотонно убывала (монотонно возрастала).
монотонно убывала (монотонно возрастала).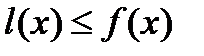 равносильно неравенству
равносильно неравенству  , (5)
, (5) равносильно неравенству
равносильно неравенству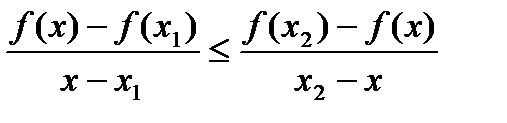 (6)
(6) ,
,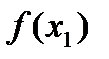 и
и 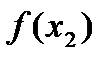 , получаем
, получаем 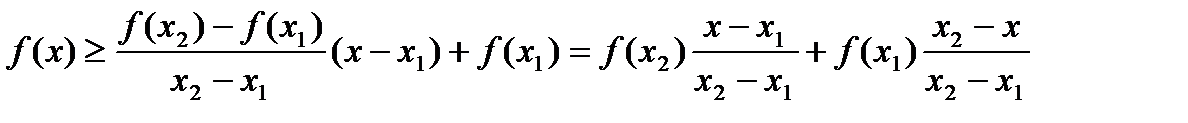 .
.
 .
.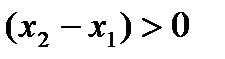 , получаем
, получаем  . Последнее неравенство делим на
. Последнее неравенство делим на 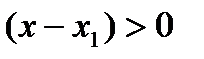 ,
, 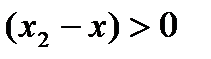 . Окончательно получаем
. Окончательно получаем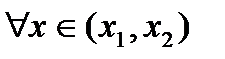 справедливо неравенство
справедливо неравенство  , получаем
, получаем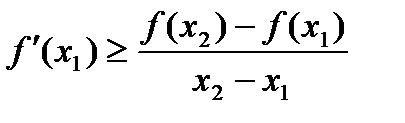 , (8)
, (8)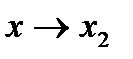 , получаем
, получаем . (9)
. (9)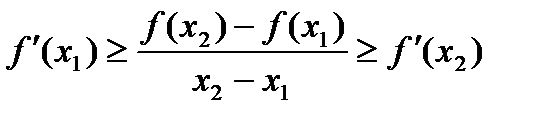 , то есть
, то есть  , то
, то ,
,  ,
,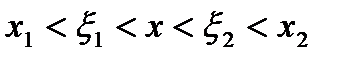 . Так как
. Так как 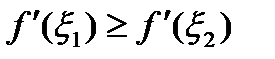 , а, следовательно,
, а, следовательно,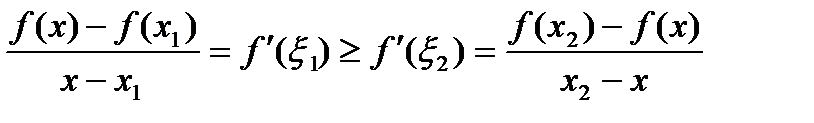 . (10)
. (10) , то вместо неравенства (8) получаем неравенство
, то вместо неравенства (8) получаем неравенство ,
, выполнялось неравенство
выполнялось неравенство  (
(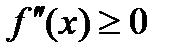 ).
).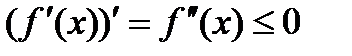 (
( . Остается применить теорему 1.
. Остается применить теорему 1. .
.
 - произвольная точка. Уравнение касательной линии к графику функции в данной точке имеет вид
- произвольная точка. Уравнение касательной линии к графику функции в данной точке имеет вид 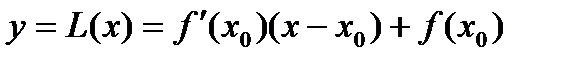 .
.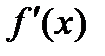 монотонно убывает на интервале
монотонно убывает на интервале 
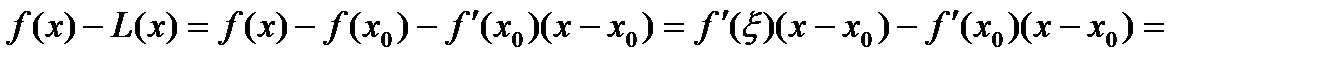
 , (11)
, (11)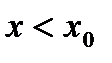
 ,
,  , а, если
, а, если 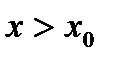 , то
, то 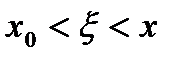 ,
, 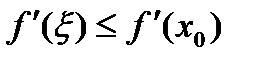 .
.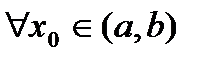 , и
, и 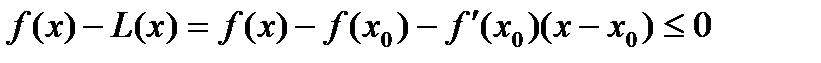 . Тогда
. Тогда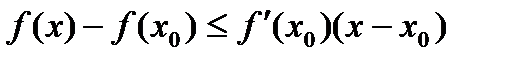 . (12)
. (12)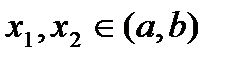 ,
,  , тогда из неравенства (12) получаем
, тогда из неравенства (12) получаем 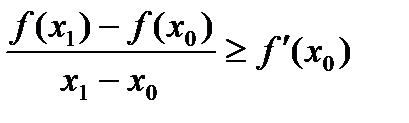 ,
, 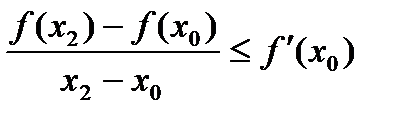 .
.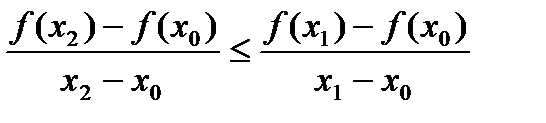 (13)
(13) 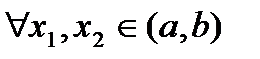 и
и  . Условие (13) является равносильным условию выпуклости вверх функции
. Условие (13) является равносильным условию выпуклости вверх функции  по лемме.
по лемме. дифференцируема в точке
дифференцируема в точке  ,
, 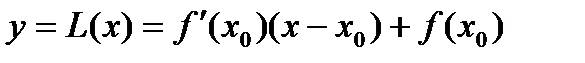 - уравнение касательной к графику функции в точке
- уравнение касательной к графику функции в точке 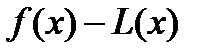 меняет знак при переходе через точку
меняет знак при переходе через точку 
 разность
разность 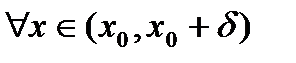 разность
разность 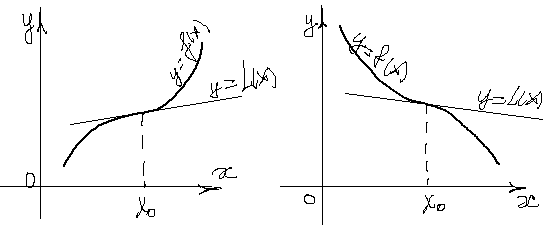
 .
.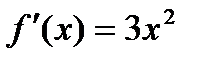 ,
, 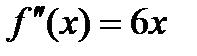 , и
, и  при
при 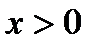 , то есть функция выпукла вниз на интервале
, то есть функция выпукла вниз на интервале  и любая касательная в точках
и любая касательная в точках  лежит ниже графика.
лежит ниже графика. при
при 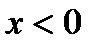 , то есть функция выпукла вверх на интервале
, то есть функция выпукла вверх на интервале 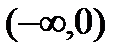 и любая касательная в точках
и любая касательная в точках  лежит выше графика функции.
лежит выше графика функции. - точка перегиба. Касательная в этой точке
- точка перегиба. Касательная в этой точке  .
.
 непрерывна в точке
непрерывна в точке  .
.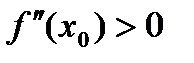 (
( ), тогда
), тогда 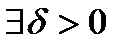
 выполняется неравенство
выполняется неравенство  (
( ), то есть на интервале
), то есть на интервале  функция выпукла вниз (вверх) и любая касательная к графику функции лежит, в силу теоремы 3, ниже (выше) графика функции, то есть
функция выпукла вниз (вверх) и любая касательная к графику функции лежит, в силу теоремы 3, ниже (выше) графика функции, то есть 


