
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Тейлора для многочлена
Пусть дан многочлен ……………………………………. Положив в этих равенствах
Аналогично, если
Формулы (1), (2) называются формулами Тейлора для многочлена.
Разложение функции по формуле Тейлора.
Пусть функция
Очевидно, Обозначим Покажем, что ЛЕММА. Если Докажем лемму методом математической индукции. Пусть
Предположим, что утверждение верно при Из верности утверждения для
Вернемся к равенству (3). В силу леммы Получаем формулу Тейлора с дополнительным членом в форме Пеано. ТЕОРЕМА 1. Пусть функция
Формула (4) называется формулой Тейлора с дополнительным членом в форме Пеано.
ЗАМЕЧАНИЕ. Формула (4) является обобщением равенства
ФОРМУЛА ТЕЙЛОРА С ДОПОЛНИТЕЛЬНЫМ ЧЛЕНОМ В ФОРМЕ ЛАГРАНЖА И КОШИ
Предположим, что функция
Фиксируем точку
где
Пусть
Так как 1. Возьмем
2. Возьмем
ТЕОРЕМА 2. Пусть функция
где
МНОГОЧЛЕН ТЕЙЛОРА КАК МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ ТЕОРЕМА. Пусть функция Замечание. Теорема утверждает, что другой многочлен не может приближать данную функцию с точностью до Доказательство. По формуле Тейлора с дополнительным членом в форме Пеано имеем
Перейдем в равенстве (8) к пределу при где Отбрасываем слева и справа равные первые слагаемые и разделим обе части равенства на
Переходя в равенстве к пределу при Повторяем такие операции, получим
Единственность разложения может быть использована для того, чтобы получить разложение каким либо косвенным путем. ПРИМЕР. Заметим, что Полагаем
ФОРМУЛЫ ТЕЙЛОРА ДЛЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ. 1.
2.
3.
4.
5.
ИССДЕДОВАНИЕ ФУНКЦИЙ
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.175.180 (0.03 с.) |
 . Найдем производные многочлена
. Найдем производные многочлена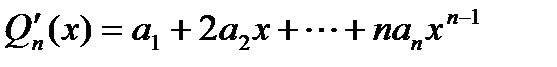 ,
, ,
,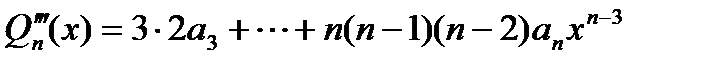 ,
,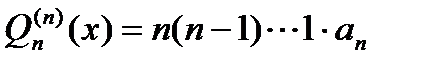 .
. , получаем
, получаем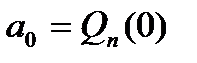 ,
,  ,
,  ,…,
,…,  . Таким образом, многочлен может быть записан в форме
. Таким образом, многочлен может быть записан в форме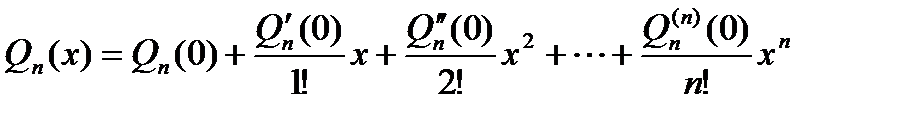 . (1)
. (1) , получаем
, получаем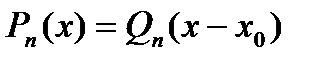 , или
, или  .
. ,
, 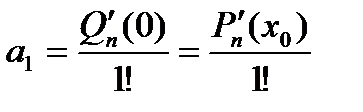 ,
,  ,…,
,…,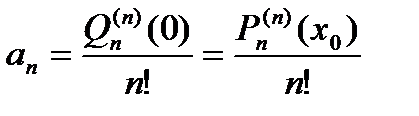 , тогда
, тогда . (2)
. (2)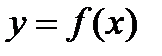 имеет производные до порядка
имеет производные до порядка 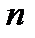 включительно
включительно  ,
, 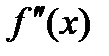 ,…,
,…, 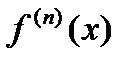 на интервале
на интервале 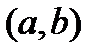 . Составим многочлен
. Составим многочлен .
.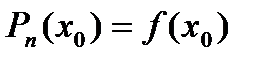 ,
, 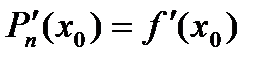 ,
, 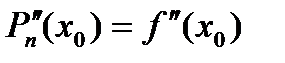 , …,
, …, 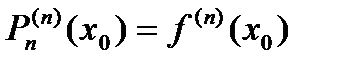 .
. . (3)
. (3) , если
, если 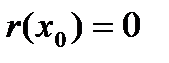 ,
,  ,
,  ,…,
,…,  .
.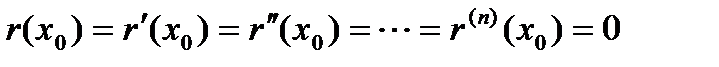 , то
, то  . Покажем, что
. Покажем, что 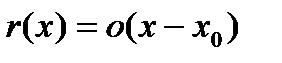 . Действительно, справедливо равенство
. Действительно, справедливо равенство .
. , покажем, что утверждение верно при
, покажем, что утверждение верно при  .
.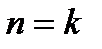 имеем
имеем 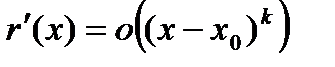 . По формуле конечных приращений Лагранжа имеем
. По формуле конечных приращений Лагранжа имеем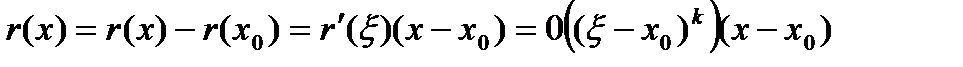 , где точка
, где точка  ,
, 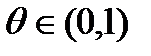 . Так как
. Так как 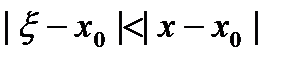 , получаем
, получаем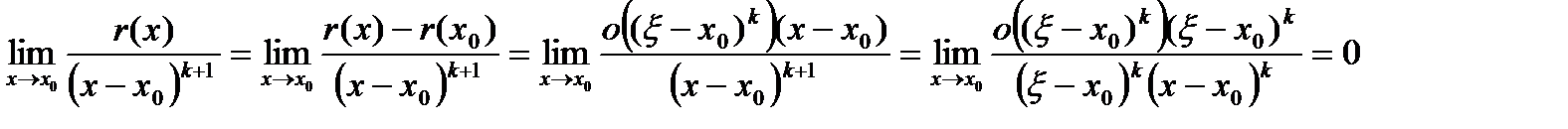 . Лемма доказана.
. Лемма доказана.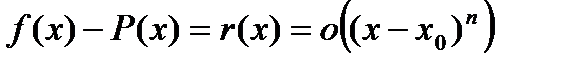 .
.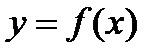
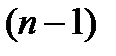 раз дифференцируема на интервале
раз дифференцируема на интервале 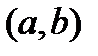 и
и 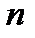 раз дифференцируема в точке
раз дифференцируема в точке 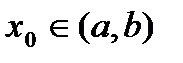 , тогда справедлива формула
, тогда справедлива формула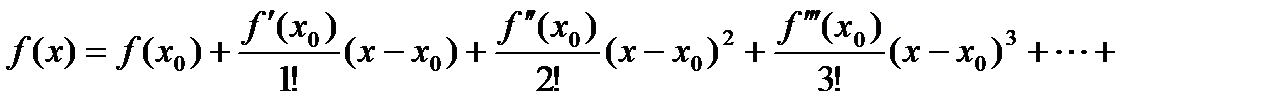
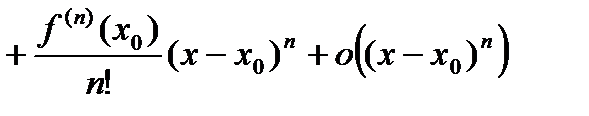 . (4)
. (4) , которое задает условие дифференцируемости функции в точке
, которое задает условие дифференцируемости функции в точке  .
.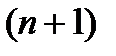 раз дифференцируема на интервале
раз дифференцируема на интервале 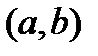 ,
,  . Рассмотрим функцию
. Рассмотрим функцию 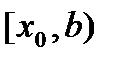 (случай полуинтервала
(случай полуинтервала 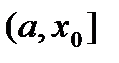 рассматривается аналогично).
рассматривается аналогично). .
. и составим вспомогательную функцию
и составим вспомогательную функцию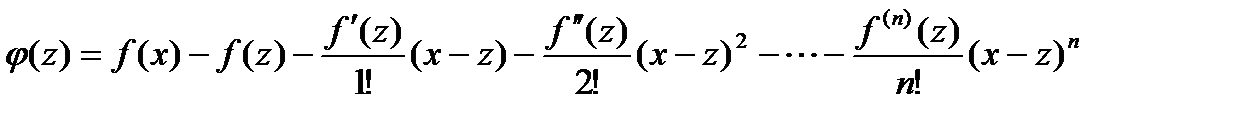 ,
,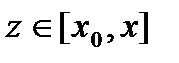 . На этом отрезке функция
. На этом отрезке функция 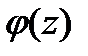 непрерывна,
непрерывна, 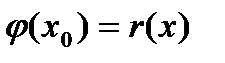 ,
, 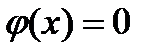 . Кроме того, на интервале
. Кроме того, на интервале  функция дифференцируема, и
функция дифференцируема, и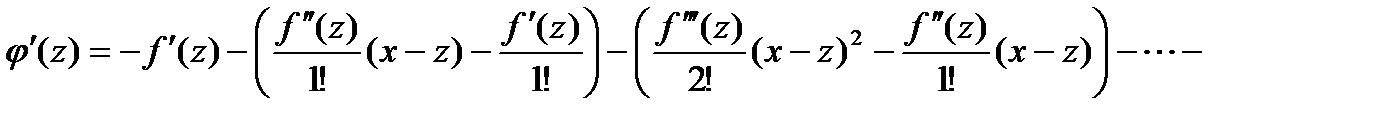
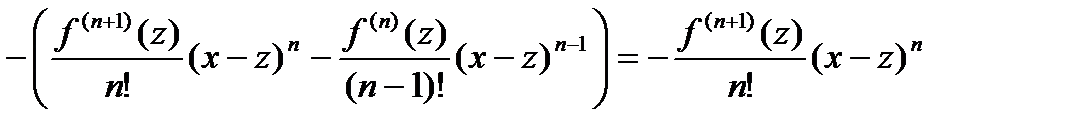 .
.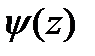 - непрерывная на отрезке
- непрерывная на отрезке  , дифференцируема на интервале
, дифференцируема на интервале 
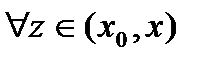 . Справедлива теорема Коши, то есть существует точка
. Справедлива теорема Коши, то есть существует точка 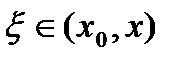 такая, что
такая, что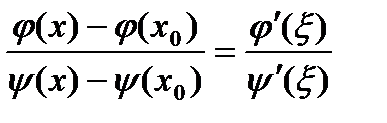 . (5)
. (5) ,
,  ,
, 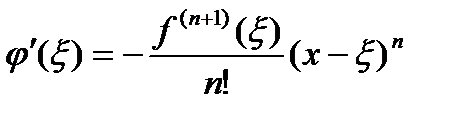 , то
, то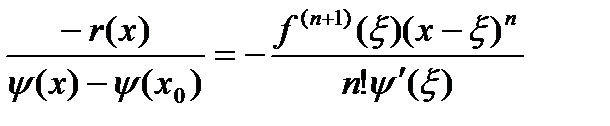 . (6)
. (6) , тогда
, тогда 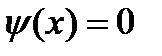 ,
,  ,
,  . Подставляя в (6), получим остаточный член в форме Лагранжа
. Подставляя в (6), получим остаточный член в форме Лагранжа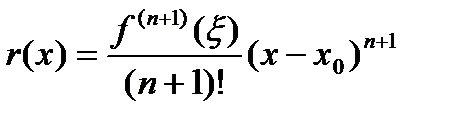 .
. , тогда
, тогда 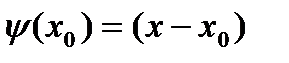 ,
,  ,
, 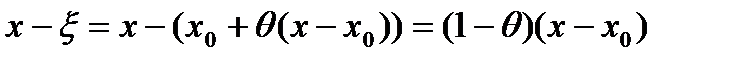 . Тогда из равенства (6) получим остаточный член в форме Коши
. Тогда из равенства (6) получим остаточный член в форме Коши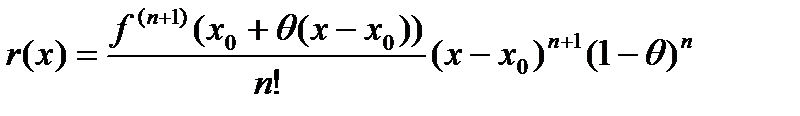 .
. справедлива формула Тейлора
справедлива формула Тейлора 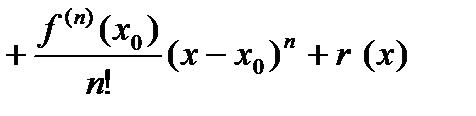 , (7)
, (7)
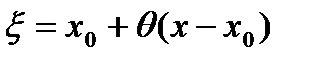 ,
, 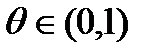 .
.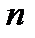 раз дифференцируема в точке
раз дифференцируема в точке  и
и 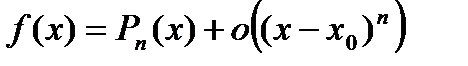 при
при 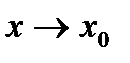 , где
, где  - многочлен степени
- многочлен степени 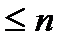 . Тогда
. Тогда 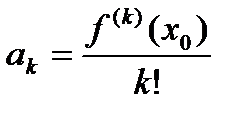 ,
,  , то есть
, то есть  - многочлен Тейлора.
- многочлен Тейлора. при
при 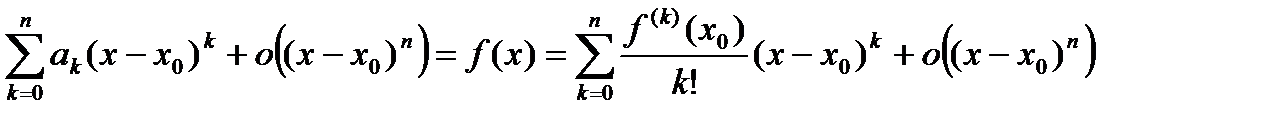 . (8)
. (8) , учитывая, что
, учитывая, что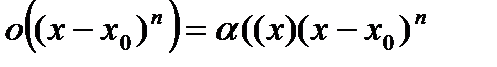 , (9)
, (9) при
при 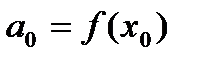 .
.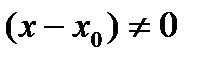 , получаем
, получаем .
.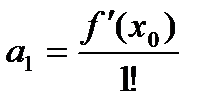 .
. ,
,  .
.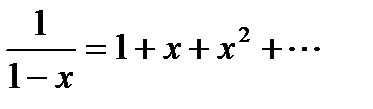 , если
, если 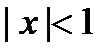 .
. , получаем
, получаем . Это и есть искомое разложение по формуле Тейлора.
. Это и есть искомое разложение по формуле Тейлора. ,
, 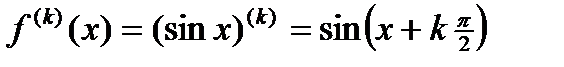 ,
, 
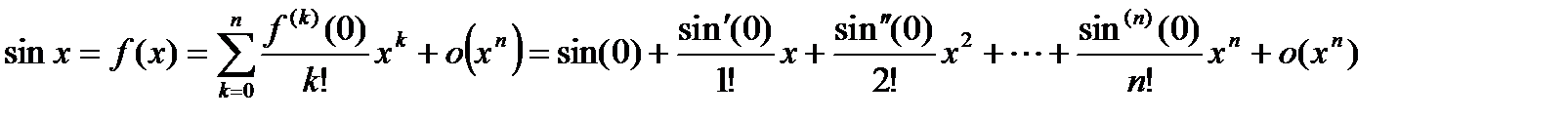 .
.  .
.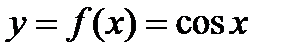 ,
, 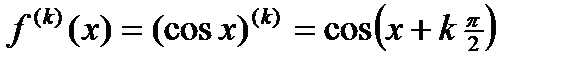 ,
,  .
.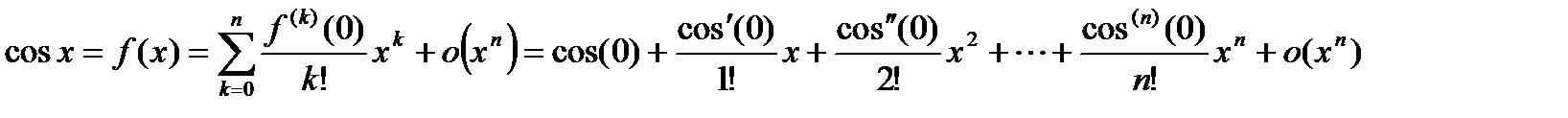 .
. .
.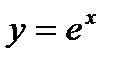 ,
,  ,
,  ,
,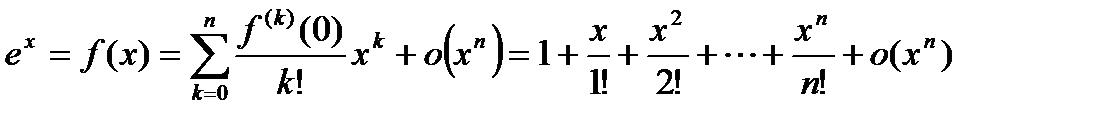 .
. ,
, 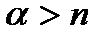 ,
, 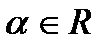
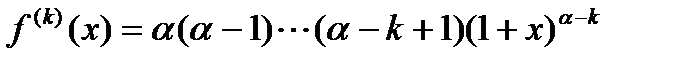 ,
,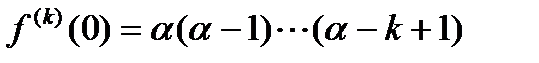 ,
, 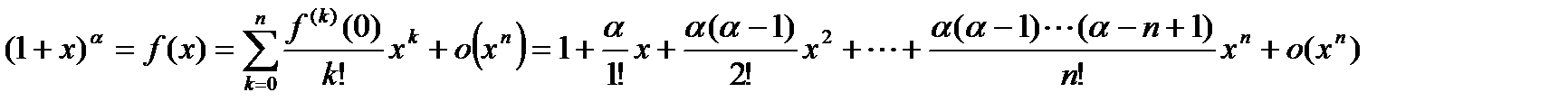
 ,
, 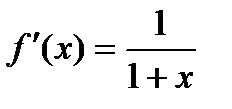 ,
,  ,
,  ,…,
,…,  ,
, 

 .
.


