Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Существование и непрерывность обратных функцийСодержание книги
Поиск на нашем сайте
Понятие функции есть частный случай понятия отображения. Мы знаем, что, если отображение
ЛЕММА. Пусть функция Доказательство. Пусть функция То, что такая точка существует, следует из того, что Докажем, что точка Докажем, что обратная функция строго монотонно возрастает (убывает). Пусть 1) 2) 3) То есть мы доказали, что обратная функция строго монотонно возрастает. Аналогично доказывается, что обратная функция строго монотонно убывает, если функция ТЕОРЕМА 1. Пусть функция
Доказательство. Докажем теорему для случая строго монотонно возрастающей функции. (В случае строго монотонно убывающей функции доказательство аналогично). Покажем, что отрезок Таким образом все значения на отрезке В силу леммы имеем, что существует обратная функция Нам остается показать, что функция непрерывна на отрезке Пусть Зафиксируем произвольное тогда в силу строгого монотонного возрастания функции получаем неравенство Пусть число Пусть
В силу строгого монотонного возрастания функции Мы получили,
Последнее означает, по определению, что функция Если Выберем То есть мы получили, Аналогично доказывается, что функция Теорема доказана. Аналогичные теоремы справедливы, если функция строго монотонна на интервале, полуинтервале конечном или бесконечном. ТЕОРЕМА 2. Пусть функция ТЕОРЕМА 3. Пусть функция
Непрерывность функции
Рассмотрим функцию
Рассмотрим функцию
Если рассматривать эту функцию на всей области определения, то есть на Однако на отрезке
так как справедливы неравенства то
Как мы показывали ранее, функция
Рассмотрим функцию
Если рассматривать эту функцию на всей области определения, то есть на Однако на отрезке
так как справедливы неравенства то
Как мы показывали ранее, функция Обратная функция
Рассмотрим функцию
Такая функция определена при всех
Рассмотрим функцию Функция определена при всех По теореме об обратной функции существует обратная функция
Показательная функция.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.007 с.) |

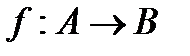 биективное, то есть взаимно-однозначное, то существует обратное отображение
биективное, то есть взаимно-однозначное, то существует обратное отображение 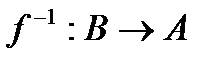 . Причем, если
. Причем, если 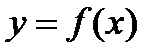 , то
, то 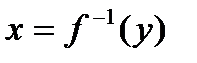 , и справедливы равенства
, и справедливы равенства 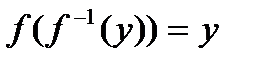 и
и 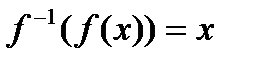 .
.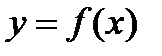 строго монотонно возрастает (убывает) на некотором множестве
строго монотонно возрастает (убывает) на некотором множестве 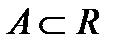 и пусть
и пусть 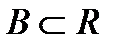 - ее множество значений, тогда существует обратная функция
- ее множество значений, тогда существует обратная функция 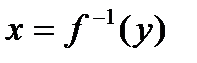 , которая является строго монотонно возрастающей (убывающей) на множестве
, которая является строго монотонно возрастающей (убывающей) на множестве 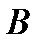 .
.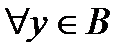
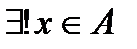 такая, что
такая, что 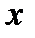 - единственная. Доказательство будем вести от противного. Предположим, что существует не одна точка, а по крайней мере две
- единственная. Доказательство будем вести от противного. Предположим, что существует не одна точка, а по крайней мере две 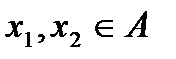 такие, что
такие, что 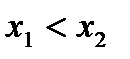 и
и 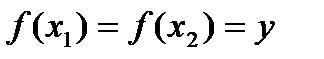 , но это противоречит строгой монотонности функции, так как
, но это противоречит строгой монотонности функции, так как 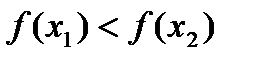 (
(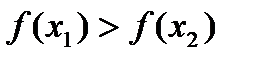 ).Так как мы получили противоречие, то наше предположение неверно. Следовательно,
).Так как мы получили противоречие, то наше предположение неверно. Следовательно, 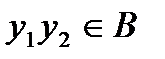 - произвольные точки такие, что
- произвольные точки такие, что 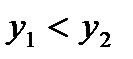 . Возможны три варианта
. Возможны три варианта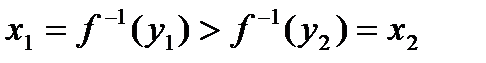 , но тогда в силу строгого монотонного возрастания функции
, но тогда в силу строгого монотонного возрастания функции 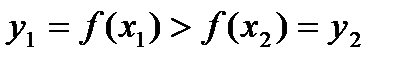 , то есть противоречие. То есть такое предположение неверно.
, то есть противоречие. То есть такое предположение неверно.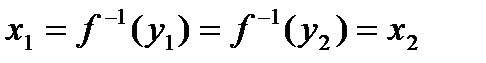 , но тогда
, но тогда 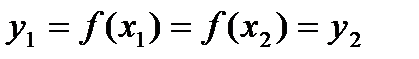 , то есть противоречие. То есть такое предположение неверно.
, то есть противоречие. То есть такое предположение неверно. , тогда
, тогда 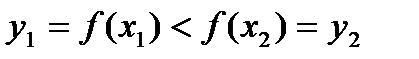 , получаем верное неравенство.
, получаем верное неравенство.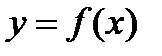 непрерывна на отрезке
непрерывна на отрезке 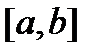 и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на отрезке
и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на отрезке 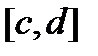 ,
, 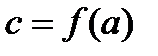 ,
, 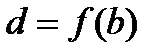 (в случае монотонно убывающей функции
(в случае монотонно убывающей функции 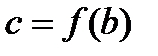 ,
, 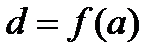 ), строго монотонно возрастает (убывает) и непрерывна на отрезке
), строго монотонно возрастает (убывает) и непрерывна на отрезке 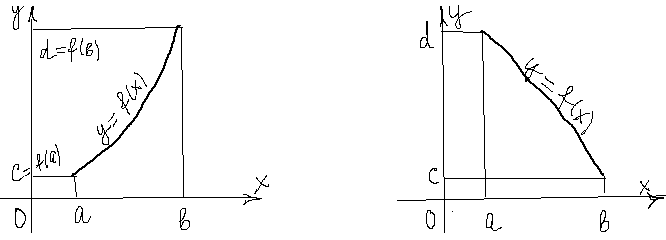
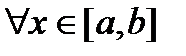 выполняется неравенство
выполняется неравенство 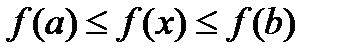 , то есть на концах отрезка
, то есть на концах отрезка 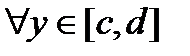
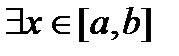 такая, что
такая, что 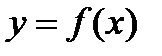 .
.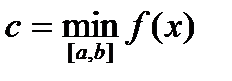 ,
, 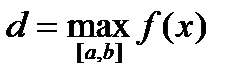 .
.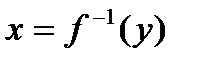 , которая определена и строго монотонно возрастает на отрезке
, которая определена и строго монотонно возрастает на отрезке 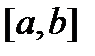 .
.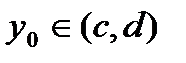 ,
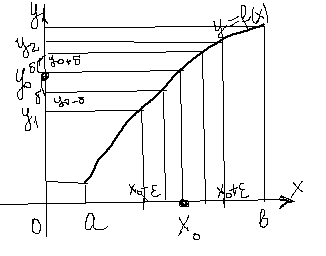
, 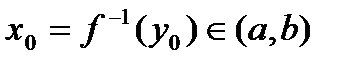 .
.
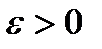 такое, чтобы справедливо было неравенство
такое, чтобы справедливо было неравенство 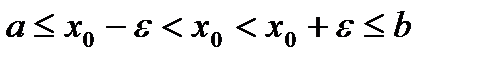 (Неравенство означает, что
(Неравенство означает, что 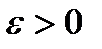 - достаточно мало, так что точки
- достаточно мало, так что точки 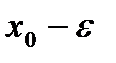 и
и 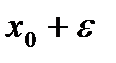 лежат на отрезке
лежат на отрезке 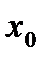 - внутренняя точка интервала
- внутренняя точка интервала 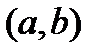 ). Пусть
). Пусть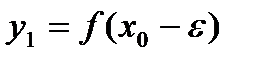 , а
, а 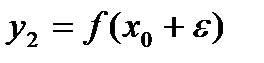 ,
,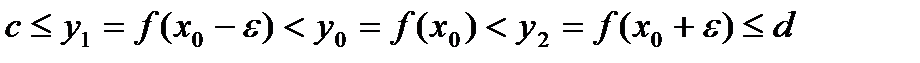 .
.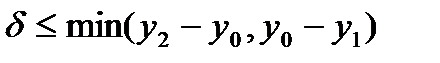 , тогда верно неравенство
, тогда верно неравенство .
.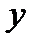 - любая точка на интервале,
- любая точка на интервале, 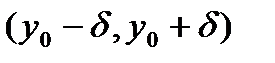 , то есть выполняется неравенство
, то есть выполняется неравенство .
. получаем неравенство
получаем неравенство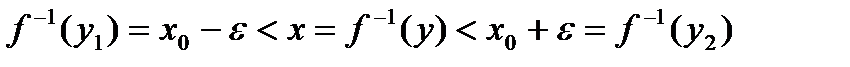 .
.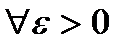
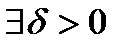 такое, что
такое, что 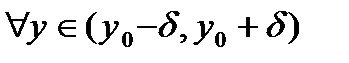
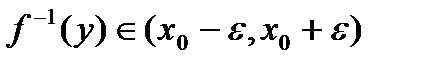 . Учитывая, что
. Учитывая, что 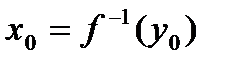 , получаем.
, получаем.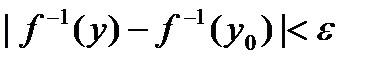 .
. .
.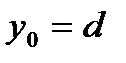 , то нам требуется доказать, что функция
, то нам требуется доказать, что функция 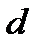 слева, то есть
слева, то есть 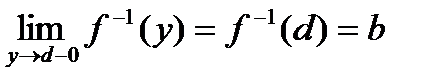 .
.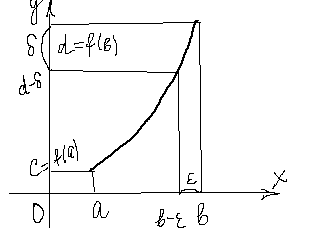
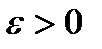 (так, чтобы точка
(так, чтобы точка 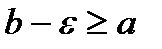 ). Тогда
). Тогда 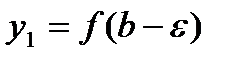 . Пусть число
. Пусть число 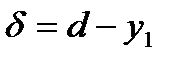 . Тогда для любого
. Тогда для любого 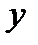 , удовлетворяющего неравенству
, удовлетворяющего неравенству 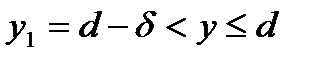 , в силу строгой монотонности функции имеем
, в силу строгой монотонности функции имеем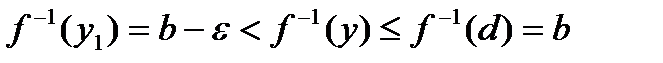 .
.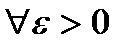
 такое, что
такое, что  выполняется
выполняется 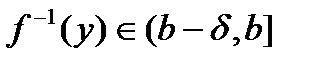 . По определению это означает, что
. По определению это означает, что
 справа.
справа.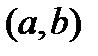 и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на интервале
и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на интервале 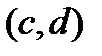 ,
, 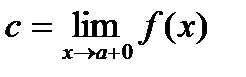 ,
, 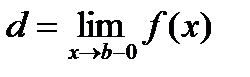 (в случае монотонно убывающей функции
(в случае монотонно убывающей функции 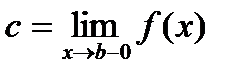 ,
, 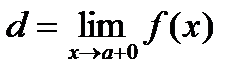 ), строго монотонно возрастает (убывает) и непрерывна на интервале
), строго монотонно возрастает (убывает) и непрерывна на интервале 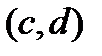 .
.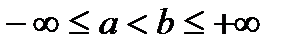 , и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на интервале
, и строго монотонно возрастает (убывает) на нем, тогда обратная функция определена на интервале 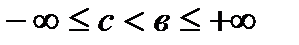 , строго монотонно возрастает (убывает) и непрерывна на интервале
, строго монотонно возрастает (убывает) и непрерывна на интервале 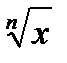 , обратных тригонометрических функций.
, обратных тригонометрических функций.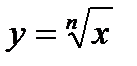 .
.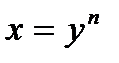 . Если её рассматривать на всей числовой оси, то она не является биективным отображением, например, при четных значениях
. Если её рассматривать на всей числовой оси, то она не является биективным отображением, например, при четных значениях 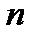 . Поэтому рассмотрим эту функцию на неограниченном полуинтервале
. Поэтому рассмотрим эту функцию на неограниченном полуинтервале 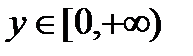 . На этом полуинтервале функция является строго монотонно возрастающей. Множество значение функции неограниченный полуинтервал
. На этом полуинтервале функция является строго монотонно возрастающей. Множество значение функции неограниченный полуинтервал 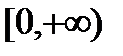 . Как было нами показано ранее функция непрерывна на полуинтервале
. Как было нами показано ранее функция непрерывна на полуинтервале 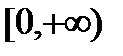 . По теореме об обратной функции
. По теореме об обратной функции  .
.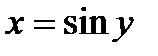 .
.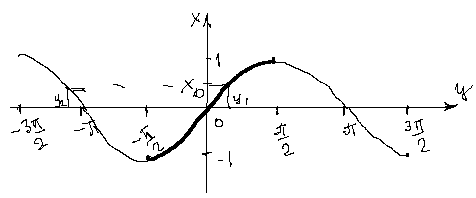
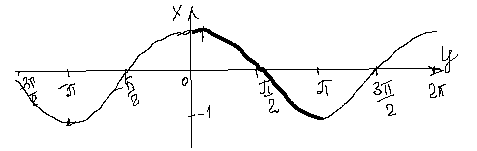
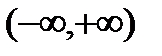 , то функция не является биективным отображением, так на рисунке показано, что значение
, то функция не является биективным отображением, так на рисунке показано, что значение 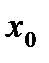 функция принимает в бесконечном числе точек.
функция принимает в бесконечном числе точек.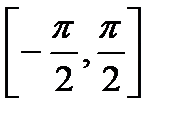 функция является строго монотонно возрастающей. В самом деле, для любых точек
функция является строго монотонно возрастающей. В самом деле, для любых точек 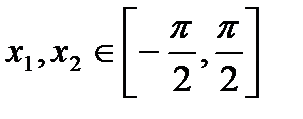 таких, что
таких, что 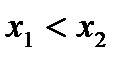 верно неравенство
верно неравенство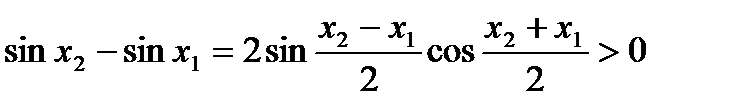 ,
,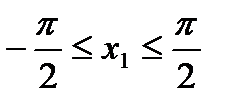 ,
, 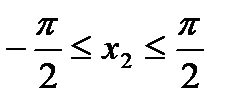 ,
,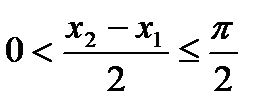 ,
, 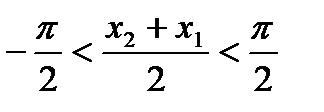 , и, поэтому
, и, поэтому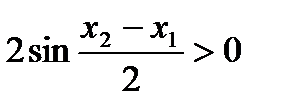 ,
, 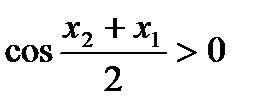 .
.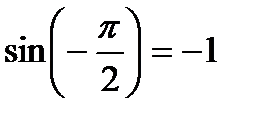 , на правом конце
, на правом конце 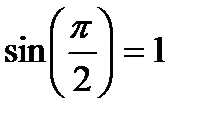 , поэтому обратная функция имеет область определения отрезок
, поэтому обратная функция имеет область определения отрезок 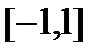 , множество значений – отрезок
, множество значений – отрезок 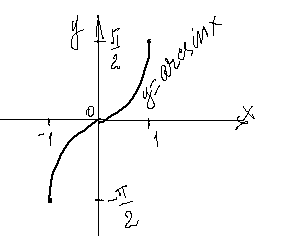
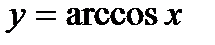
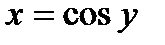
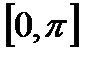 функция является строго монотонно убывающей. В самом деле, для любых точек
функция является строго монотонно убывающей. В самом деле, для любых точек 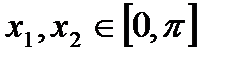 таких, что
таких, что 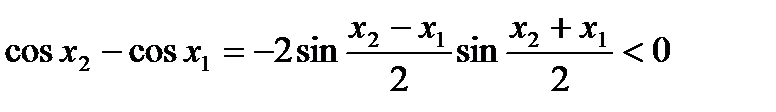 ,
,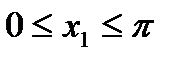 ,
, 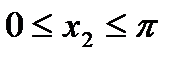 ,
,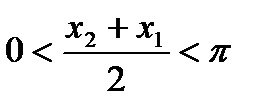 , и, поэтому
, и, поэтому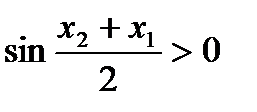 .
.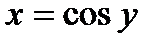 непрерывна на отрезке
непрерывна на отрезке 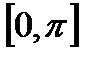 . На левом конце она принимает значение
. На левом конце она принимает значение 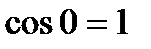 , на правом конце
, на правом конце 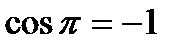 , поэтому обратная функция имеет область определения отрезок
, поэтому обратная функция имеет область определения отрезок 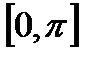 .
. 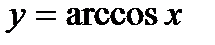 является строго монотонно убывающей непрерывной функцией на отрезке
является строго монотонно убывающей непрерывной функцией на отрезке 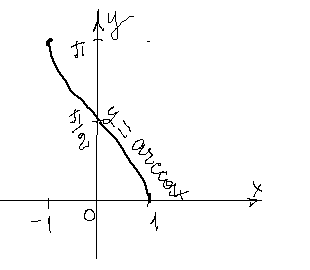
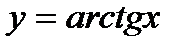
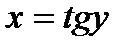
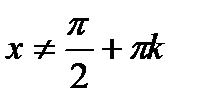 ,
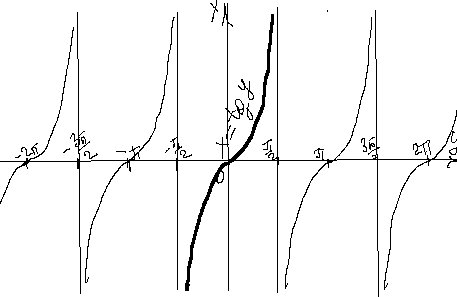
, 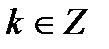 . Она не является биективной. Однако, если мы будем рассматривать функцию на интервале
. Она не является биективной. Однако, если мы будем рассматривать функцию на интервале 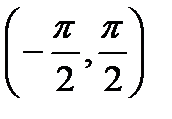 , то на этом интервале она является строго монотонно возрастающей и непрерывной, причем
, то на этом интервале она является строго монотонно возрастающей и непрерывной, причем 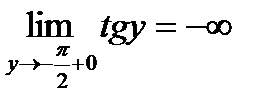 ,
, 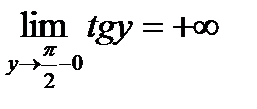 . Следовательно множество значений функции
. Следовательно множество значений функции 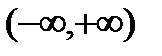 . Как было показано ранее функция
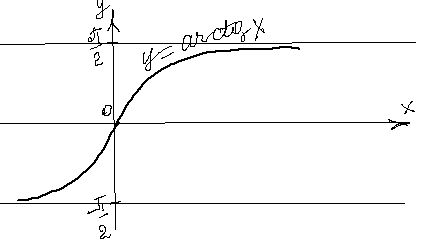
. Как было показано ранее функция 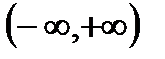 .
.
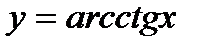
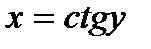 .
.
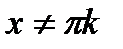 ,
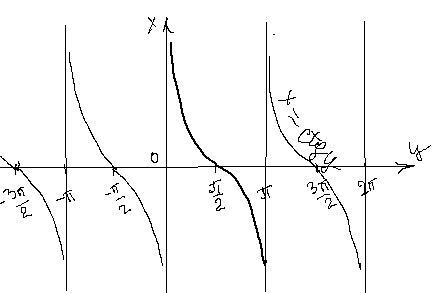
, 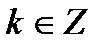 . Функция является периодической на области определения и, поэтому не является взаимно-однозначной. Если же мы рассмотрим функцию на интервале
. Функция является периодической на области определения и, поэтому не является взаимно-однозначной. Если же мы рассмотрим функцию на интервале 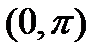 , то на таком интервале она является строго монотонно убывающей и непрерывной, причем
, то на таком интервале она является строго монотонно убывающей и непрерывной, причем  ,
, 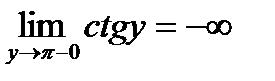 . Следовательно множество значений функции интервал
. Следовательно множество значений функции интервал 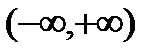 .
.