
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монотонные функции и их точки разрыва.
Пусть ОПРЕДЕЛЕНИЕ 6. Функция
ОПРЕДЕЛЕНИЕ 7. Функция
ОПРЕДЕЛЕНИЕ 8. Монотонно возрастающие и монотонно убывающие на промежутке
ОПРЕДЕЛЕНИЕ 9. Функция
ОПРЕДЕЛЕНИЕ 10. Функция
ОПРЕДЕЛЕНИЕ 11. Строго монотонно возрастающие и строго монотонно убывающие на промежутке
ТЕОРЕМА 1. Пусть функция Если функция ограничена сверху, то существует конечный предел Если функция неограниченна сверху, то Если функция ограничена снизу, то существует конечный предел Если функция неограниченна снизу, то Доказательство. Пусть функция 2) Но тогда, в силу монотонного возрастания функции, для всех Положим
Пусть функция
Замечание. В этом случае будем писать
Пусть функция 2) Но тогда, в силу монотонного возрастания функции, для всех Положим
Пусть функция
Замечание. В этом случае будем писать
Аналогичная теорема справедлива для монотонно убывающей функции.
ТЕОРЕМА 2. Пусть функция Если функция ограничена сверху, то существует конечный предел Если функция неограниченна сверху, то Если функция ограничена снизу, то существует конечный предел Если функция неограниченна снизу, то
СЛЕДСТВИЕ 1. Пусть функция Доказательство. Пусть функция Кроме того, СЛЕДСТВИЕ 2. Пусть функция Доказательство. Если односторонние пределы совпадают Если односторонние пределы не совпадают, по следствию 1 они конечны, то есть точка
ТЕОРЕМА 3 (Счетность множества точек разрыва у монотонной функции). Пусть функция
Доказательство. Пусть функция Пусть
Точке разрыва Каждой точке разрыва функции
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.014 с.) |
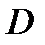 - промежуток на числовой прямой (отрезок, интервал, полуинтервал) конечный или бесконечный.
- промежуток на числовой прямой (отрезок, интервал, полуинтервал) конечный или бесконечный.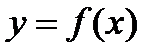 называется монотонно возрастающей на промежутке
называется монотонно возрастающей на промежутке 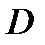 , если
, если 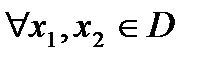 таких, что
таких, что 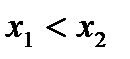 выполняется неравенство
выполняется неравенство 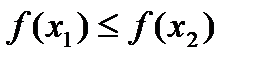 .
.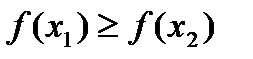 .
.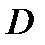 функции называются монотонными на
функции называются монотонными на  .
.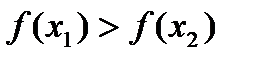 .
.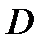 функции называются строго монотонными на
функции называются строго монотонными на  монотонно возрастает на интервале
монотонно возрастает на интервале  .
.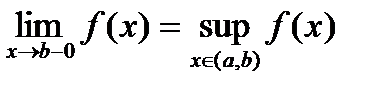 .
.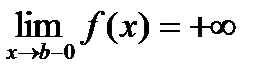 .
.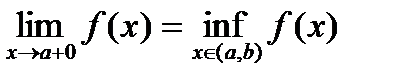 .
.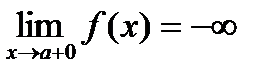 .
. . Тогда справедливы утверждения 1)
. Тогда справедливы утверждения 1) 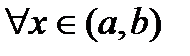
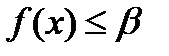 ,
,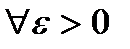

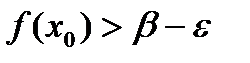 .
. 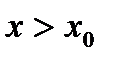 ,
, 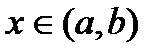 выполняется неравенство
выполняется неравенство 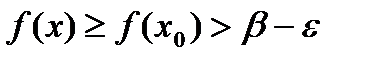 .
. . Получаем,
. Получаем, 
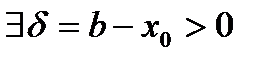
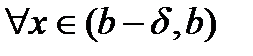 выполняется неравенство
выполняется неравенство 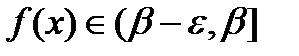 . Последнее означает, по определению,
. Последнее означает, по определению,  .
.
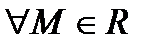
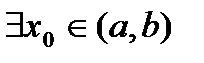 такая точка, что
такая точка, что  . В силу монотонного возрастания функции имеем
. В силу монотонного возрастания функции имеем 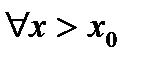 ,
, 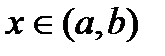
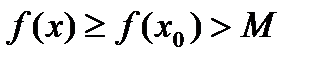 .
.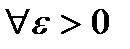 , положим
, положим  , тогда
, тогда  , что
, что 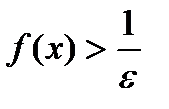 . Последнее означает, по определению,
. Последнее означает, по определению, 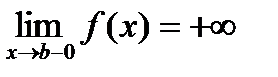 .
.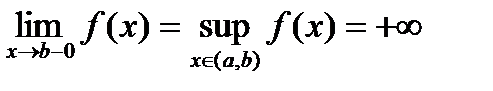 .
.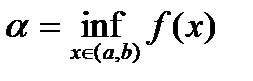 . Тогда справедливы утверждения 1)
. Тогда справедливы утверждения 1)  ,
, .
. 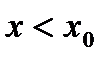 ,
, 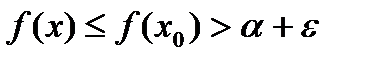 .
.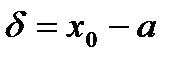 . Получаем,
. Получаем, 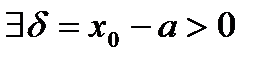
 выполняется неравенство
выполняется неравенство 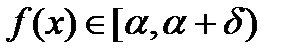 . Последнее означает, по определению,
. Последнее означает, по определению, 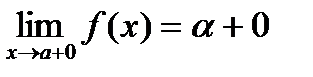 .
.
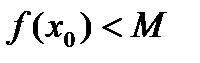 . В силу монотонного возрастания функции имеем
. В силу монотонного возрастания функции имеем  ,
, 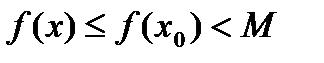 .
. , тогда
, тогда 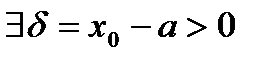 , что
, что 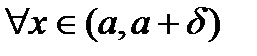 выполняется неравенство
выполняется неравенство  . Последнее означает, по определению,
. Последнее означает, по определению, 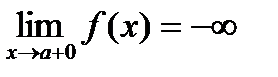 .
. .
. .
.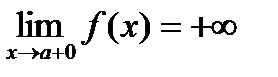 .
.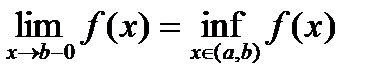 .
.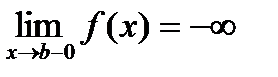 .
.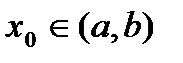 существуют конечные односторонние пределы
существуют конечные односторонние пределы 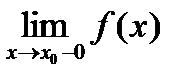 ,
, 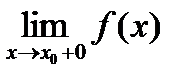 .
.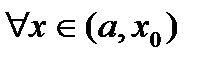 ,
, 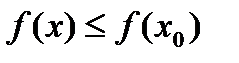 . Последнее неравенство означает, что функция
. Последнее неравенство означает, что функция 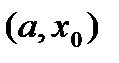 . По теореме имеем, существует предел слева
. По теореме имеем, существует предел слева  .
. ,
, 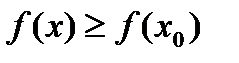 . Последнее неравенство означает, что функция
. Последнее неравенство означает, что функция  . По теореме имеем, существует предел справа
. По теореме имеем, существует предел справа  .
.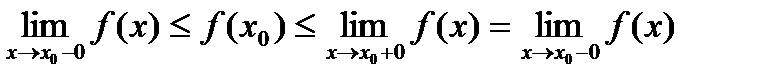 , то существует предел функции и равен значению функции в точке
, то существует предел функции и равен значению функции в точке 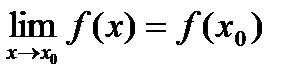 .
.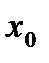 является точкой разрыва первого рода.
является точкой разрыва первого рода.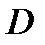 , тогда множество точек разрыва или конечное или счетное.
, тогда множество точек разрыва или конечное или счетное.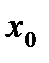 можно поставить в соответствие интервал
можно поставить в соответствие интервал 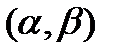 , где
, где 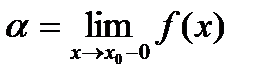 ,
, 
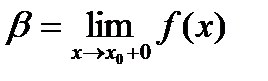 , причем справедливо неравенство
, причем справедливо неравенство 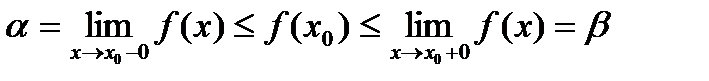 . Верно неравенство
. Верно неравенство 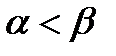 , в противном случае в точке
, в противном случае в точке 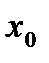 функция была бы непрерывна.
функция была бы непрерывна.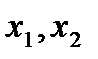 - две различные точки разрыва функции
- две различные точки разрыва функции 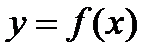 , пусть
, пусть  . Покажем, что этим точкам соответствуют разные интервалы, причем непересекающиеся.
. Покажем, что этим точкам соответствуют разные интервалы, причем непересекающиеся. ставится в соответствие интервал
ставится в соответствие интервал 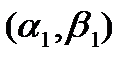 , где
, где 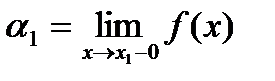
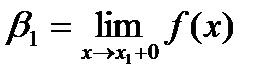 . Точке разрыва
. Точке разрыва 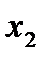 ставится в соответствие интервал
ставится в соответствие интервал 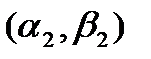 , где
, где 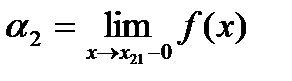
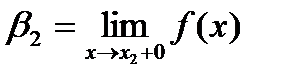 . Пусть точка
. Пусть точка 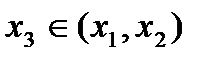 тогда справедливо неравенство
тогда справедливо неравенство 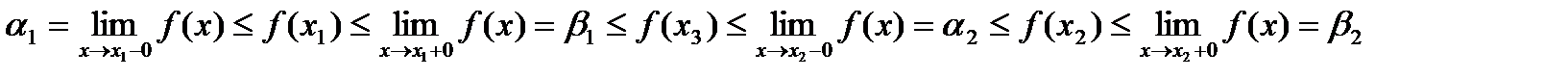 .
. 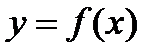 поставим интервал взаимно однозначно, каждому интервалу поставим в соответствие рациональное число
поставим интервал взаимно однозначно, каждому интервалу поставим в соответствие рациональное число 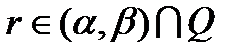 . Поскольку интервалы не пересекаются, то это соответствие взаимно однозначное. Поскольку множество рациональных чисел счетное, то его подмножество или счетное или конечное. Поэтому множество точек разрыва монотонной функции или счетное или конечное. Теорема доказана.
. Поскольку интервалы не пересекаются, то это соответствие взаимно однозначное. Поскольку множество рациональных чисел счетное, то его подмножество или счетное или конечное. Поэтому множество точек разрыва монотонной функции или счетное или конечное. Теорема доказана.


