
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показательная функция и её Свойства
Свойства функции
1. Область определения показательной функции Если
2. Функция является строго монотонно возрастающей, если
Пусть Обозначим Пусть Если Если По теореме о предельном переходе в неравенстве, переходя к пределу в неравенствах (10) и (11), получаем
3.
Пусть
4.
Пусть
5.
Пусть
6.
Для доказательства непрерывности функции нам потребуется лемма. ЛЕММА 3. Доказательство. В силу леммы 2 имеем, Пусть
Из неравенств (12) и (13) получаем То есть справедливо утверждение Доказательство непрерывности функции будем проводить по определению непрерывности в терминах приращений. Составим приращение функции в точке
Так как
7. Множество значений функции интервал Для доказательства свойства достаточно показать, что если
если По определению, если Пусть
Если выполняется неравенство Получаем, Аналогично доказываются и остальные пределы. Графики функции
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
Как мы показали выше, показательная По теореме об обратной функции, существует обратная функция
В частных случаях, если Свойства логарифмической функции. 1. 2. Свойства 1, 2 следуют из определения обратной функции. 3. 4.
5.
6.
ЛИТЕРАТУРА 1. Кудрявцев Л.Д. Курс математического анализа. Т.1, § 7.
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
ТЕОРЕМА. Доказательство. Ранее было доказано, что Пусть последовательность Обозначим Тогда справедливо неравенство Прибавляем ко всем частям неравенства 1, получаем Используя свойства монотонности показательной функции с основанием больше единицы и степенной функции, получаем
Найдем предел правой части неравенства (3) Найдем предел левой части неравенства (3) В силу теоремы о трех пределах Так как Пусть теперь
В силу произвольности последовательности Из (4) и (5), так как односторонние пределы равны, следует Теорема доказана.
СЛЕДСТВИЕ 1. Доказательство. В силу свойств логарифмической функции имеем
СЛЕДСТВИЕ 2. Доказательство. Функция Применяем теорему о замене переменных в пределах, получаем
СЛЕДСТВИЕ 3. При
РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ ОПРЕДЕЛЕНИЕ. Функция ПРИМЕР 1. Рассмотрим функцию
То есть,
ТЕОРЕМА. Если функция равномерно непрерывна на множестве В самом деле, если мы зафиксируем произвольную точку Обратное утверждение неверно. ПРИМЕР 2. Покажем, что функция Рассмотрим две последовательности Последнее по определению означает
Получаем, Следовательно, функция не является равномерно непрерывной на интервале
ТЕОРЕМА (КАНТОРА). Если функция Доказательство. Доказательство будем вести от противного. Предположим, что функция не является равномерно непрерывной на отрезке Выберем такие, что Мы получили две последовательности По теореме Больцано-Вейерштрасса из ограниченной последовательности можно выделить сходящуюся подпоследовательность. То есть Из неравенства (6) следует, что Функция
Из неравенства (7) получаем Переходя в последнем неравенстве к пределу при
Литература 1. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Т. 1,гл. 4.
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.70.93 (0.058 с.) |
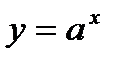 ,
, 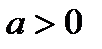 .
.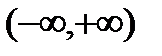 .
. , то
, то 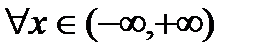 степень
степень  определена.
определена.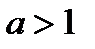 , и строго монотонно убывающей, если
, и строго монотонно убывающей, если 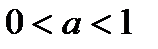 , то есть
, то есть таких, что
таких, что 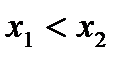
 , если
, если 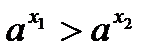 , если
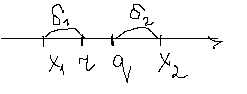
, если  такие, что
такие, что 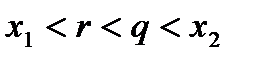 .
. 
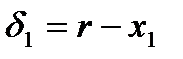 ,
, 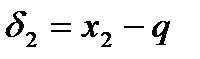 .
.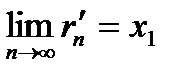 ,
, 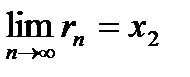 , причем
, причем 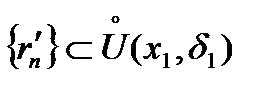 ,
,  . Тогда справедливо неравенство
. Тогда справедливо неравенство  . (9)
. (9)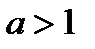 , то справедливо неравенство
, то справедливо неравенство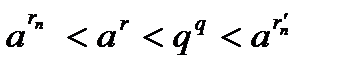 . (10)
. (10)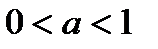 , то справедливо неравенство
, то справедливо неравенство . (11)
. (11) при
при  при
при 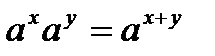 .
.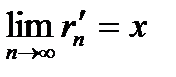 ,
, 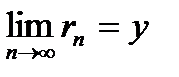 .
.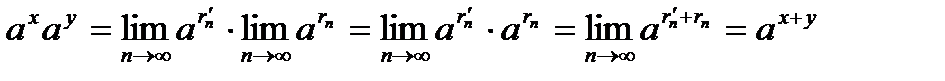 . Свойство доказано.
. Свойство доказано.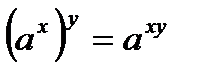 .
.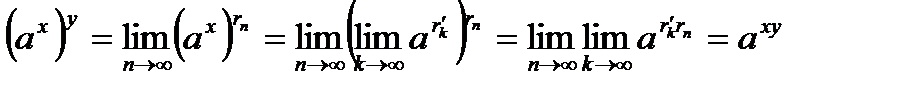 . Свойство доказано.
. Свойство доказано.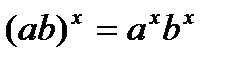 .
.  .
. . Свойство доказано.
. Свойство доказано.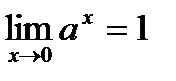 ,
, 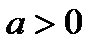 .
.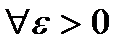
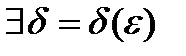 такое число, что для любого рационального числа
такое число, что для любого рационального числа 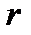 такого, что
такого, что 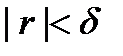 выполняется неравенство
выполняется неравенство 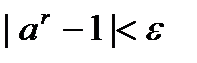 .
.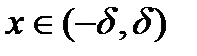 . Тогда существует
. Тогда существует 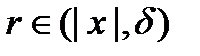 , тогда справедливо неравенство
, тогда справедливо неравенство 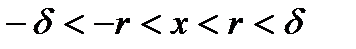 , и, в силу свойства 2 функции
, и, в силу свойства 2 функции  , получаем неравенство
, получаем неравенство , если
, если  и (12)
и (12)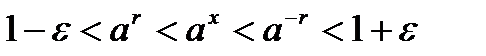 , если
, если  . (13)
. (13)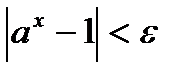 .
.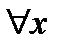 такого, что
такого, что 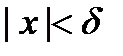 , по определению это означает, что
, по определению это означает, что 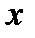 .
.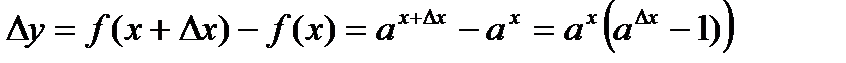 .
. , то функция непрерывна в любой точке
, то функция непрерывна в любой точке  , то есть функция непрерывна на всей области определения.
, то есть функция непрерывна на всей области определения. .
.  ,
, 
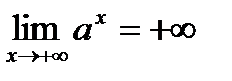 ,
, 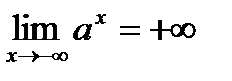 ,
, 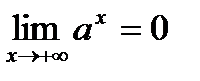 .
.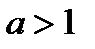 ,
, 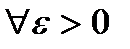
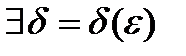 такое, что
такое, что 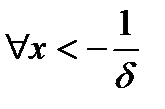 выполняется
выполняется 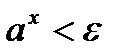 .
.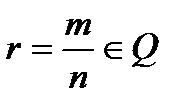 , такое рациональное число, что выполняется неравенство
, такое рациональное число, что выполняется неравенство 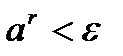 . Последнее неравенство означает, что
. Последнее неравенство означает, что 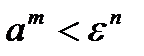 .
.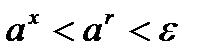 , то, по свойству функции, получаем
, то, по свойству функции, получаем  . Из последнего неравенства следует
. Из последнего неравенства следует 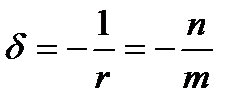 .
. такое, что
такое, что 
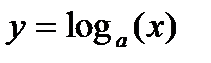 ,
, 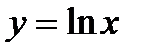
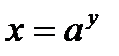 - функция определена на всей числовой оси
- функция определена на всей числовой оси 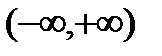 , непрерывна на области определения, строго монотонно возрастающая, если
, непрерывна на области определения, строго монотонно возрастающая, если  , и строго монотонно убывающая, если
, и строго монотонно убывающая, если 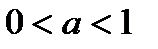 . Множеством значений является интервал
. Множеством значений является интервал 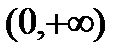 .
.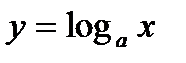 , определенная на интервале
, определенная на интервале 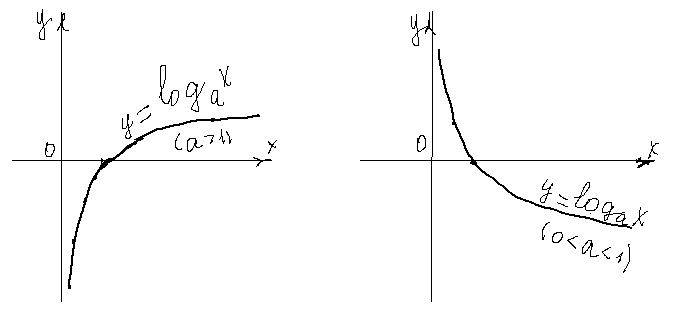
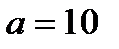 ,
, 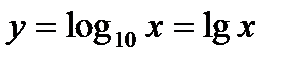 , называется десятичным логарифмом. Если
, называется десятичным логарифмом. Если 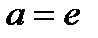 , то функция
, то функция 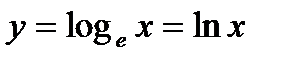 называется натуральным логарифмом.
называется натуральным логарифмом.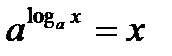 ,
, 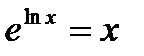 .
.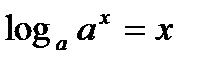 ,
, 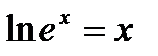 .
. ,
, 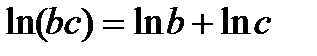 .
.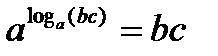 ,
, 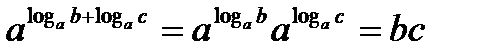 , отсюда следует, что
, отсюда следует, что  . Последнее равенство доказывает свойство.
. Последнее равенство доказывает свойство. .
.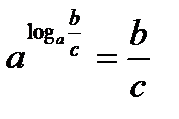 ,
, 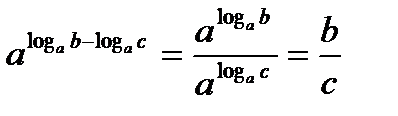 , отсюда следует, что
, отсюда следует, что 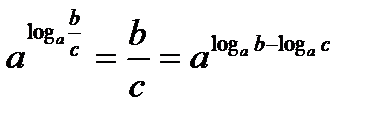 . Последнее равенство доказывает свойство.
. Последнее равенство доказывает свойство. .
.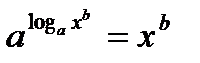 ,
,  . Свойство доказано.
. Свойство доказано.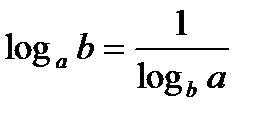 .
.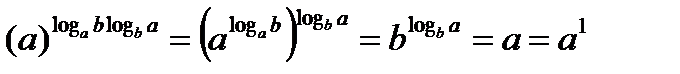 , отсюда получаем
, отсюда получаем  . Свойство доказано.
. Свойство доказано. .
.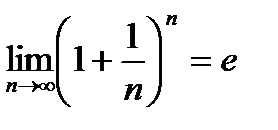 , тогда
, тогда  имеем
имеем 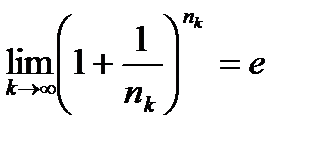 .
.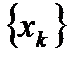 - последовательность такая, что
- последовательность такая, что 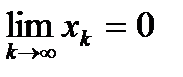 ,
,  (без ограничения общности будем считать, что
(без ограничения общности будем считать, что  ), то есть
), то есть  . Тогда
. Тогда 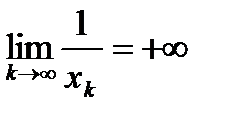 .
.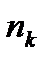 целую часть числа
целую часть числа  , то есть справедливо неравенство
, то есть справедливо неравенство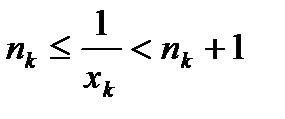 . (1)
. (1)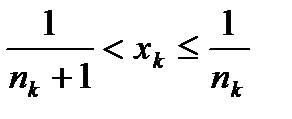 . (2)
. (2)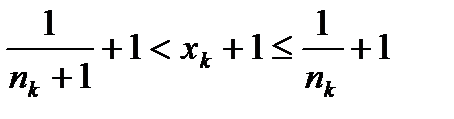 .
.  . (3)
. (3)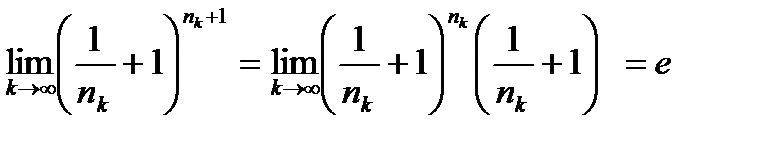 .
. .
.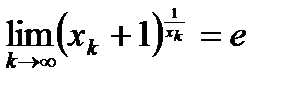 .
.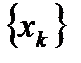 - произвольная последовательность,
- произвольная последовательность, 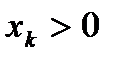 ,
, 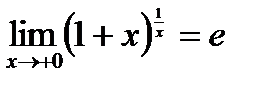 . (4)
. (4) , положим
, положим  .
.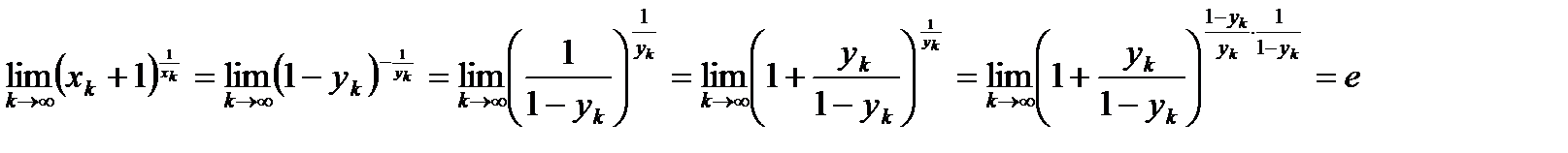 .
.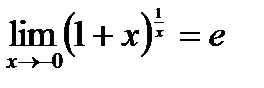 . (5)
. (5) ,
, 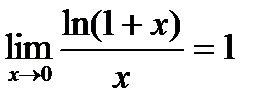 .
.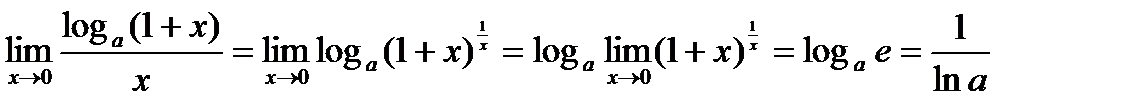 .
.  ,
, 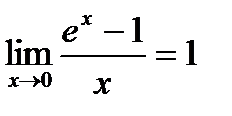 .
.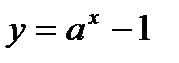 является строго монотонной. Обратная к ней функция имеет вид
является строго монотонной. Обратная к ней функция имеет вид  .
.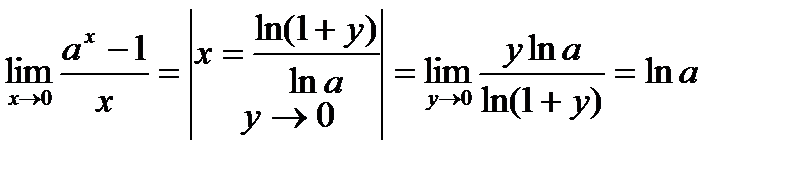 .
.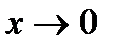
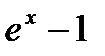 ̴
̴ 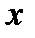 ,
, 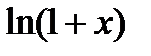 ̴
̴ 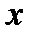 .
. называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве  , если
, если 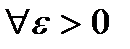
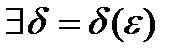
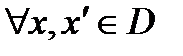 таких, что
таких, что  справедливо неравенство
справедливо неравенство 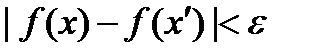 .
.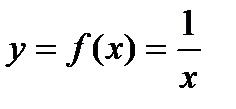 . Покажем, что функция равномерно непрерывна на интервале
. Покажем, что функция равномерно непрерывна на интервале 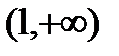 .
. .
.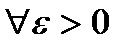
 такое, что
такое, что  выполняется неравенство
выполняется неравенство 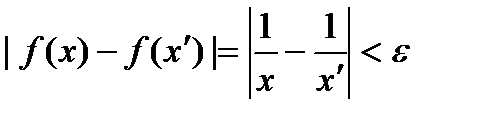 . Следовательно, функция равномерно непрерывна на интервале
. Следовательно, функция равномерно непрерывна на интервале 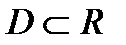 , то она непрерывна на
, то она непрерывна на 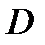 .
.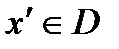 , то в силу равномерной непрерывности
, то в силу равномерной непрерывности 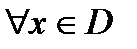 такой, что
такой, что 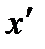 . В силу произвольности точки
. В силу произвольности точки 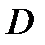 .
.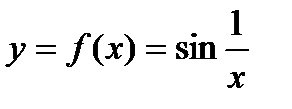 не является равномерно непрерывной на интервале
не является равномерно непрерывной на интервале 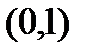 .
. ,
,  . Очевидно, что
. Очевидно, что  ,
, 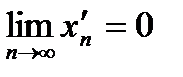 , тогда
, тогда  .
.
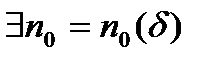 такой номер, что
такой номер, что  выполняется неравенство
выполняется неравенство  .
.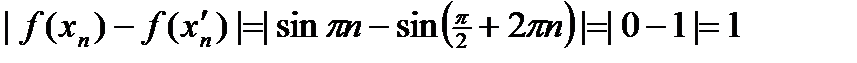 .
.
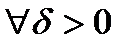
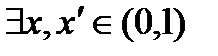 (
(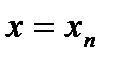 ,
, 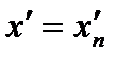 ,
, 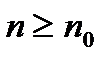 ) такие, что
) такие, что 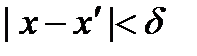 , а
, а 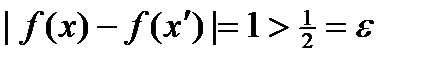 .
. непрерывна на отрезке
непрерывна на отрезке 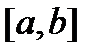 , то она равномерно непрерывна на нем.
, то она равномерно непрерывна на нем.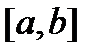 . Это значит, что
. Это значит, что 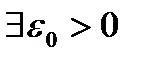 такое, что
такое, что 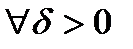
 :
: 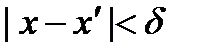 , что выполняется неравенство
, что выполняется неравенство 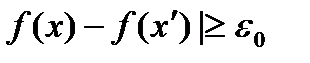 .
.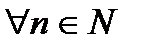 число
число 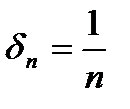 , тогда
, тогда 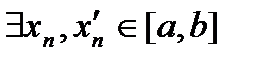 :
: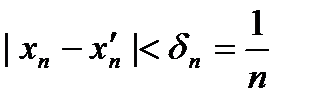 (6)
(6)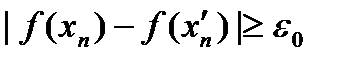 . (7)
. (7)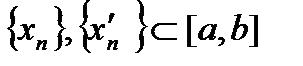 , то есть ограниченные последовательности.
, то есть ограниченные последовательности.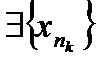 ,
,  . Из последовательности
. Из последовательности 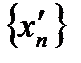 выделим подпоследовательность с теми же номерами
выделим подпоследовательность с теми же номерами 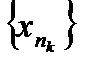 .
.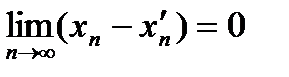 , тогда любая подпоследовательность сходится, и
, тогда любая подпоследовательность сходится, и 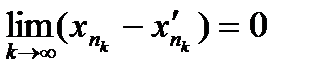 .
. .
.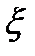 . В силу определения по Гейне получаем
. В силу определения по Гейне получаем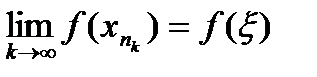 ,
, 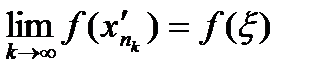 . (8)
. (8)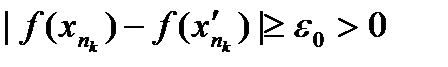 .
.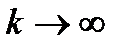 , получаем
, получаем 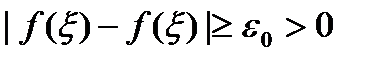 . Получили противоречие, следовательно, наше предположение неверно. Теорема доказана.
. Получили противоречие, следовательно, наше предположение неверно. Теорема доказана.


