
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о непрерывных функциях
ОПРЕДЕЛЕНИЕ 1. Функция
ОПРЕДЕЛЕНИЕ 2. Функция
ОПРЕДЕЛЕНИЕ 3. Функция
ОПРЕДЕЛЕНИЕ 4. Функция
ТЕОРЕМА Вейерштрасса (первая). Пусть функция Доказательство. Чтобы доказать, что функция ограничена на отрезке достаточно доказать, что функция ограничена сверху и ограничена снизу. Докажем, что функция ограничена сверху, то есть Таким образом, мы построили последовательность Так как последовательность Так как справедливо неравенство Последнее равенство противоречит равенству (2). То есть предположение неверно, а это означает, что функция ограниченна сверху. Аналогично доказывается, что функция ограниченна снизу. Теорема доказана.
ТЕОРЕМА Вейерштрасса (вторая). Пусть функция
Доказательство. Докажем, что существует точка Из последнего неравенства получаем для
ТЕОРЕМА Больцано-Коши (о промежуточных значениях непрерывной функции). Пусть функция Доказательство теоремы. Пусть Если Если Если Разделим отрезок Если Если Если Продолжаем процесс дальше. Или на каком то шаге получим точку Поскольку верно неравенство С другой стороны, по свойству пределов имеем
То есть По теореме о сжимающейся системе вложенных отрезков
В силу определения непрерывности функции в точке Переходим к пределу в неравенстве (4), получаем Отсюда имеем
СЛЕДСТВИЕ 1. Пусть функция СЛЕДСТВИЕ 2. Пусть функция Доказательство. По второй теореме Вейрштрасса найдутся точки Тогда по теореме Больцано-Коши функция на отрезке
ОБРАТНЫЕ ФУНКЦИИ.
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.129.100 (0.018 с.) |
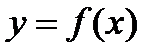 называется непрерывной на интервале
называется непрерывной на интервале 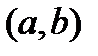 , если она непрерывна в любой точке
, если она непрерывна в любой точке 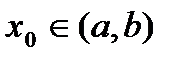 .
. , если она непрерывна в любой точке
, если она непрерывна в любой точке  и непрерывна слева в точке
и непрерывна слева в точке 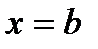 .
.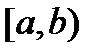 , если она непрерывна в любой точке
, если она непрерывна в любой точке  .
. , если она непрерывна в любой точке
, если она непрерывна в любой точке  и непрерывна справа в точке
и непрерывна справа в точке 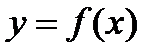 непрерывна на отрезке
непрерывна на отрезке  , тогда функция ограничена на отрезке.
, тогда функция ограничена на отрезке. , что
, что  выполняется неравенство
выполняется неравенство  . Доказательство будем вести от противного, то есть предположим, что функция неограниченна на отрезке
. Доказательство будем вести от противного, то есть предположим, что функция неограниченна на отрезке 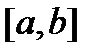 . Это означает, что
. Это означает, что 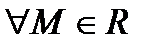
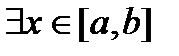 такая, что
такая, что 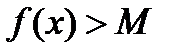 . Поскольку константа
. Поскольку константа  любая, выбарем последовательность таких констант
любая, выбарем последовательность таких констант 
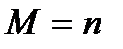 , тогда для каждого натурального числа
, тогда для каждого натурального числа 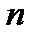 найдется точка
найдется точка  такая, что выполняется неравенство
такая, что выполняется неравенство  . (1)
. (1) , причем, если мы применим теорему о предельном переходе в неравенстве (1), то
, причем, если мы применим теорему о предельном переходе в неравенстве (1), то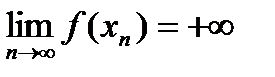 . (2)
. (2) ограниченна, то, по теореме Больцано-Вейерштрасса, из этой последовательности можно выделить сходящуюся подпоследовательность
ограниченна, то, по теореме Больцано-Вейерштрасса, из этой последовательности можно выделить сходящуюся подпоследовательность 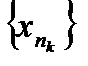 . Пусть
. Пусть 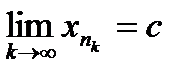 .
. , то по теореме о предельном переходе в неравенстве имеем
, то по теореме о предельном переходе в неравенстве имеем  . То есть точка
. То есть точка 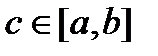 , и, поэтому функция непрерывна в этой точке. В силу определения непрерывности функции в точке по Гейне имеем
, и, поэтому функция непрерывна в этой точке. В силу определения непрерывности функции в точке по Гейне имеем  . (3)
. (3)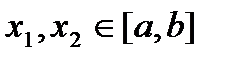 такие, что
такие, что  ,
,  .
.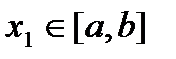 такая, что
такая, что  . Предположим противное, то есть
. Предположим противное, то есть  выполняется строгое неравенство
выполняется строгое неравенство 
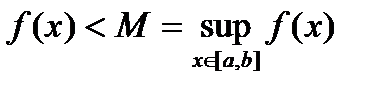 . Введем вспомогательную функцию
. Введем вспомогательную функцию 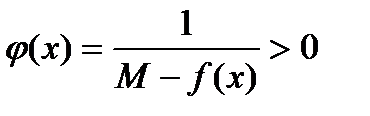 . Функция непрерывна на отрезке
. Функция непрерывна на отрезке  как частное непрерывных функций. По первой теореме Вейерштрасса функция
как частное непрерывных функций. По первой теореме Вейерштрасса функция 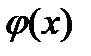 ограничена на отрезке, то есть существует положительная константа
ограничена на отрезке, то есть существует положительная константа 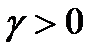 такая, что для
такая, что для  выполняется неравенство
выполняется неравенство 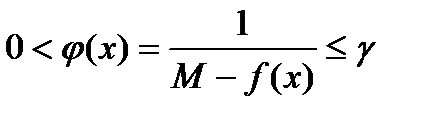 .
.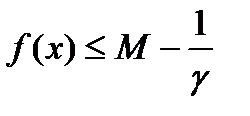 . Последнее неравенство противоречит тому, что
. Последнее неравенство противоречит тому, что 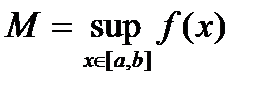 . Следовательно предположение неверно. То есть существует точка
. Следовательно предположение неверно. То есть существует точка 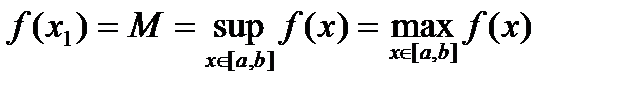 . Аналогично доказывается, что существует точка
. Аналогично доказывается, что существует точка 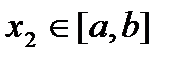 такая, что
такая, что  .
.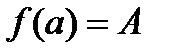 ,
,  ,
, 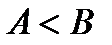 (или
(или 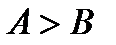 ), тогда
), тогда  (или
(или 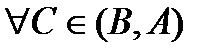 ) найдется точка
) найдется точка 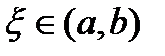 такая, что
такая, что  .
. пополам.
пополам.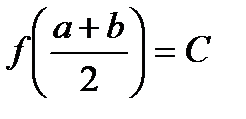 , то
, то 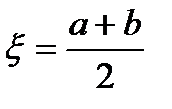 .
. , обозначим
, обозначим  ,
,  .
. 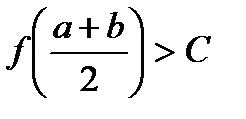 , обозначим
, обозначим 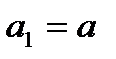
 . Получаем
. Получаем  , кроме того справедливо неравенство
, кроме того справедливо неравенство 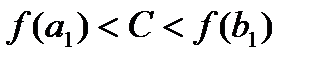 .
.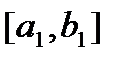 пополам.
пополам. , то
, то  .
. , обозначим
, обозначим  ,
, 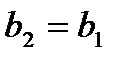 .
.  , обозначим
, обозначим 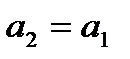
 . Получаем
. Получаем 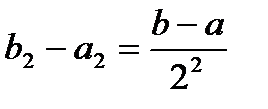 , кроме того справедливо неравенство
, кроме того справедливо неравенство  .
.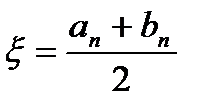 такую, что
такую, что  , или построим систему вложенных отрезков
, или построим систему вложенных отрезков 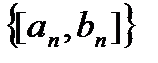 такую, что
такую, что  , причем справедливо неравенство
, причем справедливо неравенство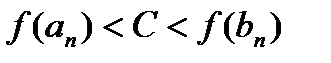 . (4)
. (4)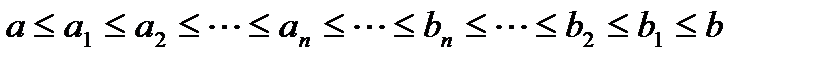 , мы получаем, что последовательность
, мы получаем, что последовательность  - монотонно возрастает и ограничена сверху, поэтому существует предел
- монотонно возрастает и ограничена сверху, поэтому существует предел  , а последовательность
, а последовательность  - монотонно убывает и ограничена снизу, поэтому существует предел
- монотонно убывает и ограничена снизу, поэтому существует предел 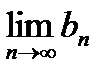 .
. .
. .
. .
.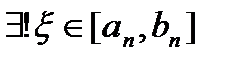
 , то есть
, то есть . Отсюда получаем
. Отсюда получаем 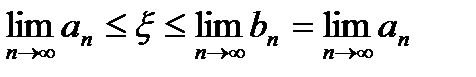 , то есть
, то есть  .
. по Гейне имеем
по Гейне имеем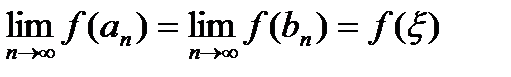 .
.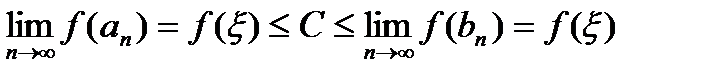 .
.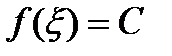 . Теорема доказана.
. Теорема доказана.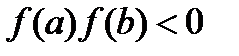 , тогда найдется точка
, тогда найдется точка 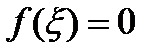 .
.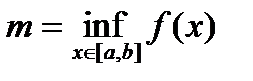 ,
, 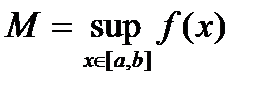 , тогда отрезок
, тогда отрезок 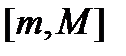 - множество значений функции.
- множество значений функции.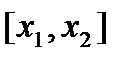 (или
(или  ) принимает любое значение
) принимает любое значение  .
.


