
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
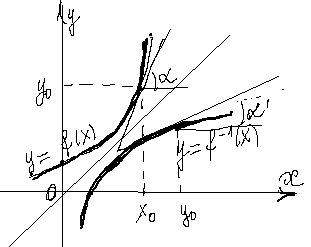
Геометрический смысл теоремы. Если графики функций и изобразить на одной плоскости
Если графики функций
причем
ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ. 1.
2.
3.
4.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ (СУПЕРПОЗИЦИИ ФУНКЦИЙ) ТЕОРЕМА. Пусть функция Замечание. Формула производной сложной функции можно записать и в другой форме Доказательство. Функции Положим Функция где Положим в равенстве Функция Поделим обе части равенства (4) на
Функция Переходя к пределу в равенстве (5), получаем
ПРИМЕР 1.
ПРИМЕР 2.
СВОЙСТВО ИНВАРИАНТНОСТИ ПЕРВОГО ДИФФЕРЕНЦИАЛА Пусть функция Дифференциал функции где Дифференциал сложной функции
но учитывая, что где Сравнивая (6) и (9), мы видим, что дифференциал функции В этом и состоит свойство инвариантности первого дифференциала.
ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕ ЯВНО Используя формулу дифференцирования сложной функции, можно находить производную функции, заданной неявно. Пусть дано уравнение Такое уравнение может задавать функцию ПРИМЕР 1. Продифференцируем равенство, считая, что Отсюда получаем ПРИМЕР 2. Прологарифмируем равенство
ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕ СКИ ОПРЕДЕЛЕНИЕ. Пусть функции ТЕОРЕМА. Если функции Доказательство. По правилу дифференцирования сложной функции имеем По теореме о дифференцировании обратной функции справедливо равенство Теорема доказана.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
ОПРЕДЕЛЕНИЕ 1. Пусть функция Аналогично определяется производная порядка ОПРЕДЕЛЕНИЕ 2. Пусть функция
ОПРЕДЕЛЕНИЕ 3. Функция (При этом если конец промежутка принадлежит промежутку, то под производной на конце понимается односторонняя производная). ПРИМЕР 1.
ПРИМЕР 2.
ПРИМЕР 3.
ПРИМЕР 4.
ТЕОРЕМА. Пусть функции (В формуле (2) под производной порядка Доказательство. Формулы доказываются по индукции. При Предполагаем, что формула верна при Тогда при
При Предполагаем, что формула верна при Используя правила вычисления производной суммы и произведения, получаем при
так как Теорема доказана.
СЛЕДСТВИЕ. Если
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.13 (0.045 с.) |
 и
и  изобразить на одной плоскости, то они симметричны относительно биссектрисы первого и третьего координатных углов. Обозначим
изобразить на одной плоскости, то они симметричны относительно биссектрисы первого и третьего координатных углов. Обозначим  угол между осью
угол между осью  и касательной к графику функции
и касательной к графику функции  , а
, а 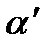 - угол между осью
- угол между осью  . Очевидно,
. Очевидно,  .
. ,
, ,
, 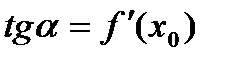 .
. ,
, 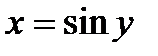 ,
, 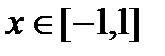 ,
,  .
. .
. ,
,  ,
,  ,
, 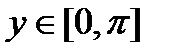 .
. .
.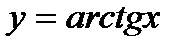 ,
,  ,
,  ,
,  .
.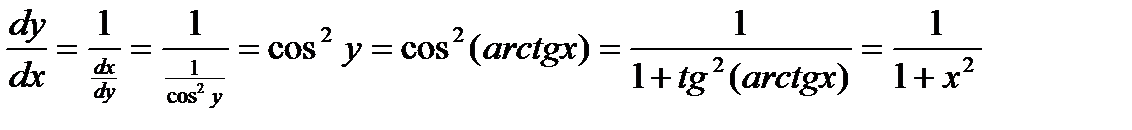 .
. ,
, 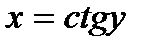 ,
, 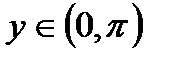 .
.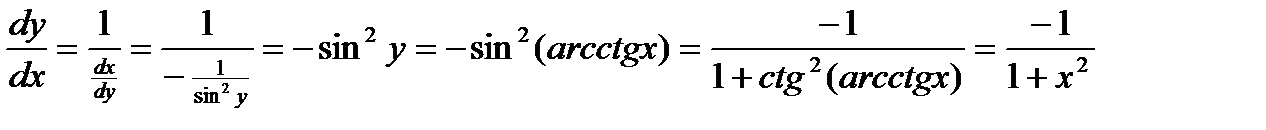 .
.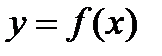 имеет производную в точке
имеет производную в точке 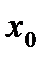 , а функция
, а функция  имеет производную в точке
имеет производную в точке  , тогда сложная функция
, тогда сложная функция  имеет производную в точке
имеет производную в точке  .
. .
.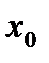 и
и 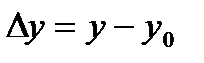 ,
, 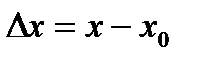 .
.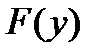 дифференцируема в точке
дифференцируема в точке  ,
,  .
.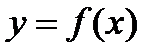 , получим
, получим , (4)
, (4) может быть не определена при
может быть не определена при 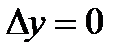 . Доопределим её, положив
. Доопределим её, положив  . Определенная таким образом функция
. Определенная таким образом функция 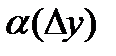 непрерывна в точке
непрерывна в точке 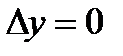 . Положим
. Положим  .
. , получаем
, получаем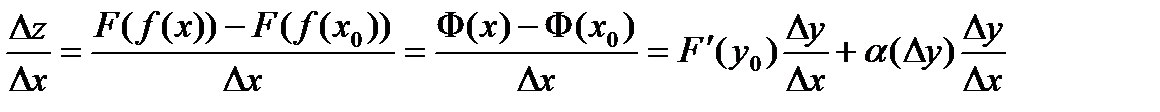 . (5)
. (5) 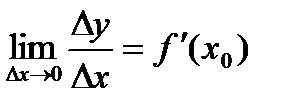 . Кроме того, функция
. Кроме того, функция 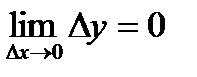 . По теореме о замене переменной в пределе имеем
. По теореме о замене переменной в пределе имеем .
.
 . Теорема доказана.
. Теорема доказана. ,
, 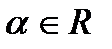 .
. ,
, 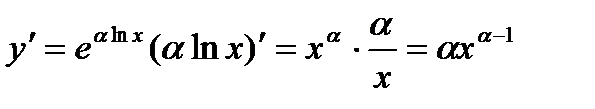 .
. , где
, где  ,
, 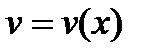 - дифференцируемые функции,
- дифференцируемые функции, 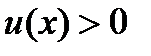 . Найти производную функции.
. Найти производную функции. ,
, 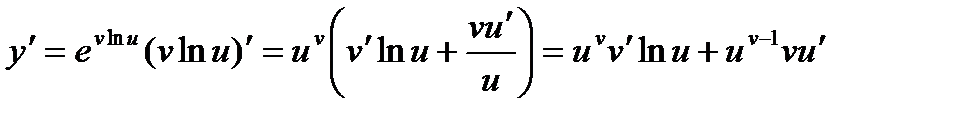 .
. , (6)
, (6)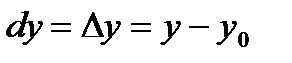 . (7)
. (7) , (8)
, (8)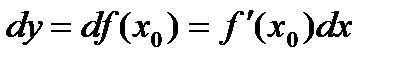 , из (8) получаем
, из (8) получаем - независимая переменная, и если
- независимая переменная, и если  - функция. Но в первом случае
- функция. Но в первом случае  - это дифференциал независимой переменной, то есть
- это дифференциал независимой переменной, то есть  , а во втором случае
, а во втором случае  - дифференциал функции.
- дифференциал функции.  .
. . Если подставить эту функцию в уравнение, то получится тождественное равенство.
. Если подставить эту функцию в уравнение, то получится тождественное равенство. .
.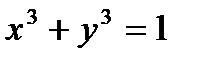 .
. , и при таком
, и при таком 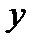 равенство превращается в тождество.
равенство превращается в тождество.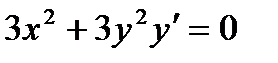 .
. .
. . Тогда
. Тогда 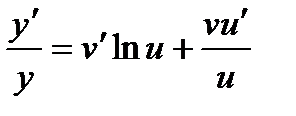 (логарифмическая производная),
(логарифмическая производная), 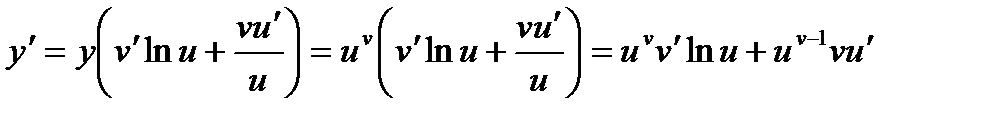 .
.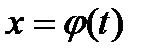 ,
,  определены в некоторой окрестности точки
определены в некоторой окрестности точки 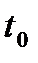 , и одна из них, например,
, и одна из них, например,  в некоторой окрестности точки
в некоторой окрестности точки  , тогда сложная функция
, тогда сложная функция  будет определена в некоторой окрестности точки
будет определена в некоторой окрестности точки 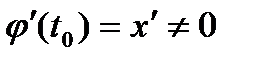 , то функция
, то функция  .
.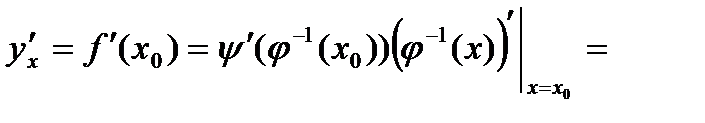 (10)
(10)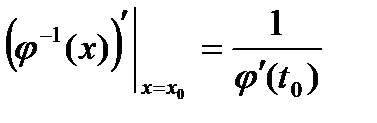 . Тогда из (10) получаем
. Тогда из (10) получаем .
.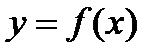 , определенная на интервале
, определенная на интервале 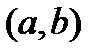 , в каждой точке интервала имеет производную
, в каждой точке интервала имеет производную 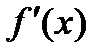 . Если
. Если 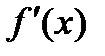 имеет производную в точке
имеет производную в точке 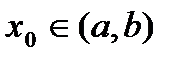 , то эта производная называется второй производной функции
, то эта производная называется второй производной функции 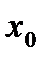 и обозначается
и обозначается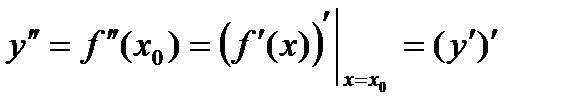 .
.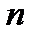 .
.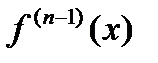 порядка
порядка 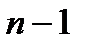 . Если
. Если 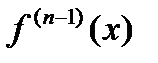 имеет производную в точке
имеет производную в точке 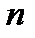 функции
функции 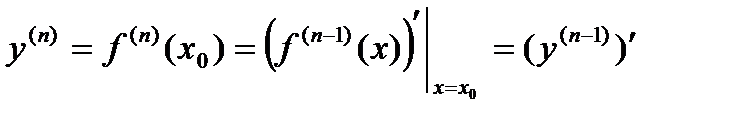 , то есть
, то есть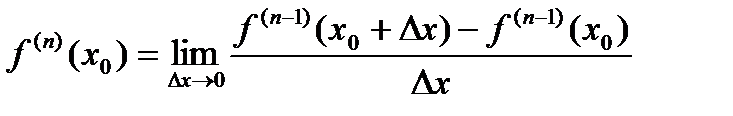 .
.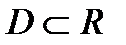 , если во всех точках этого промежутка она имеет непрерывные производные до порядка
, если во всех точках этого промежутка она имеет непрерывные производные до порядка 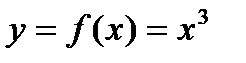 .
.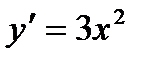 ,
, 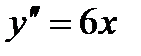 ,
, 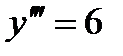 ,
, 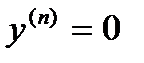 , если
, если 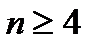 .
.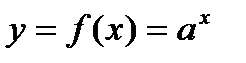 .
.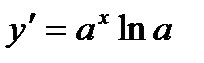 ,
, 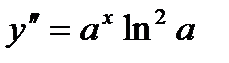 ,
, 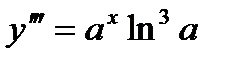 ,…,
,…, 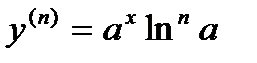 .
.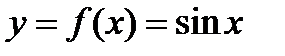 .
.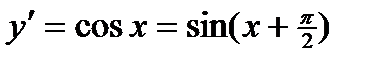 ,
, 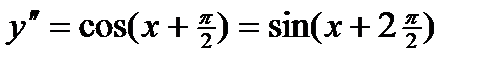 ,…,
,…, 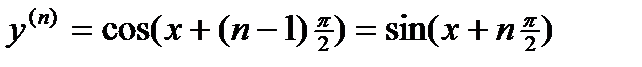 .
. .
. ,
,  ,…,
,…,  .
. и
и 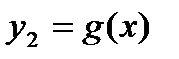 имеют в точке
имеют в точке 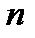 , тогда функции
, тогда функции 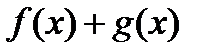 и
и 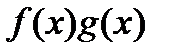 также имеют в точке
также имеют в точке  , (1)
, (1) . (Формула Лейбница) (2)
. (Формула Лейбница) (2) понимается сама функция, то есть
понимается сама функция, то есть  ).
). формула (1) верна,
формула (1) верна, 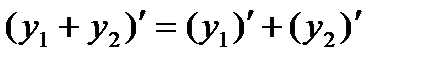 .
.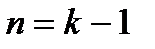 , то есть
, то есть 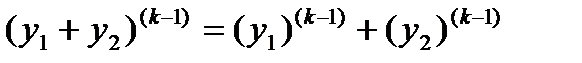 .
. получаем
получаем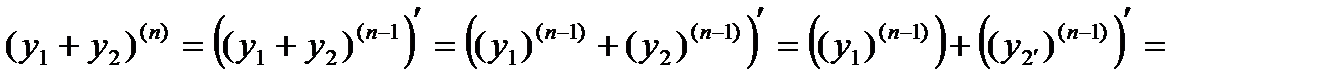
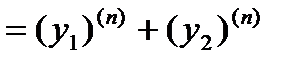 .
.  .
.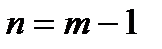 , то есть
, то есть  .
.



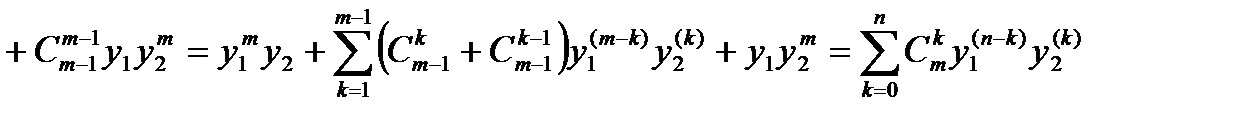 ,
, ,
,  .
. , то
, то  .
.


