
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл проиводной и дифференциала
ПРИМЕР 1. Пусть Применение дифференциала основано на том, что замена приращения функции её дифференциалом позволяет заменить любую дифференцируемую функцию линейной в достаточно малой окрестности.
ПРИМЕР 2. Пусть дан стержень. Масса части стержня от начала до точки
Если
ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Пусть функции 1. Если существуют производные Доказательство.
2. Если существуют производные Доказательство.
СЛЕДСТВИЕ. Если
Равенство получаем, так как
ЛЕММА. Если функция Доказательство. Докажем лемму от противного, то есть предположим, что Выберем последовательность чисел
3. Если существуют производные
ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ ТЕОРЕМА. Пусть функция
Доказательство. Зафиксируем окрестность точки
Так как существует предел правой части равенства
то существует предел левой части, и справедливо равенство
Используя другое обозначение производной, получаем равенство
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.141 (0.007 с.) |
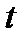 - время,
- время,  - смещение точки относительно начального положения, то есть
- смещение точки относительно начального положения, то есть 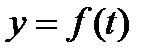 и
и  - расстояние, которое проходит точка за время
- расстояние, которое проходит точка за время  , начиная с момента времени
, начиная с момента времени 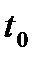 .
. - средняя скорость движения точки за время
- средняя скорость движения точки за время  величина
величина 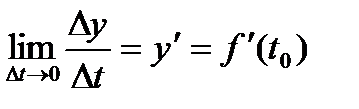 называется скоростью в точке
называется скоростью в точке 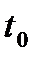 , или мгновенной скоростью.
, или мгновенной скоростью. - путь, который прошла бы точка, если бы двигалась равномерно за время
- путь, который прошла бы точка, если бы двигалась равномерно за время  (на малых участках движение можно считать равномерным).
(на малых участках движение можно считать равномерным). равна
равна  . Тогда
. Тогда  масса части стержня длины
масса части стержня длины  . Величина
. Величина  - средняя линейная плотность стерня.
- средняя линейная плотность стерня.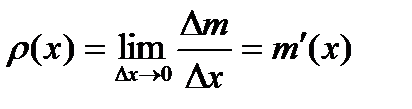 - линейная плотность стержня в точке.
- линейная плотность стержня в точке. , то стержень однородный. Если же нет, то
, то стержень однородный. Если же нет, то , то есть на малой длине стержня
, то есть на малой длине стержня 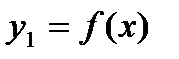 ,
,  определены в окрестности точки
определены в окрестности точки  .
. ,
,  , тогда в точке
, тогда в точке 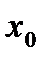 существует производная функции
существует производная функции  , причем
, причем . (1)
. (1)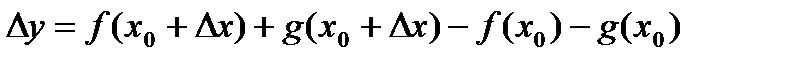 ,
,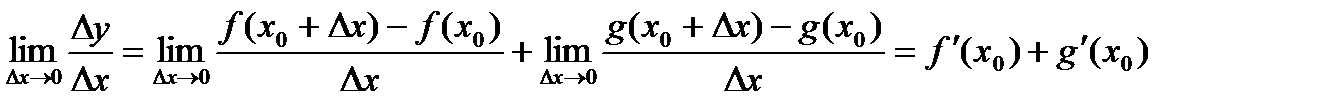 .
. , причем
, причем . (2)
. (2)

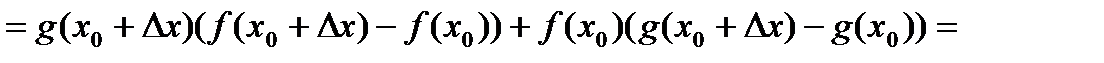
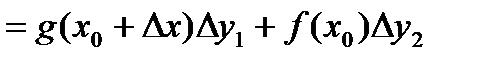 ,
,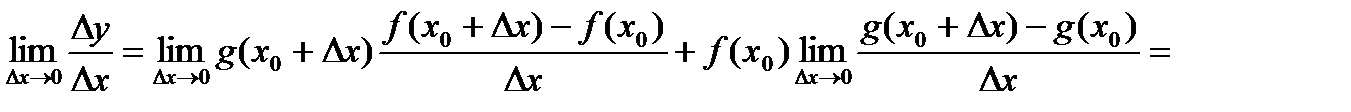
 .
. , и существует производная
, и существует производная 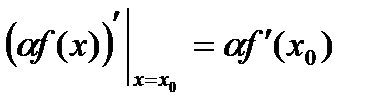 .
.
 непрерывна в точке
непрерывна в точке  и
и  , то существует
, то существует  такое, что
такое, что 
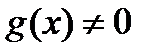 .
.
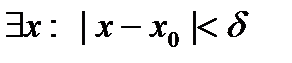
 .
.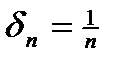 , тогда
, тогда 
 . Тогда
. Тогда  , и, в силу непрерывности функции в точке
, и, в силу непрерывности функции в точке  . Получили противоречие. Следовательно, предположение неверно. Лемма доказана.
. Получили противоречие. Следовательно, предположение неверно. Лемма доказана. , тогда в точке
, тогда в точке 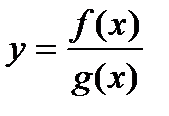 , причем
, причем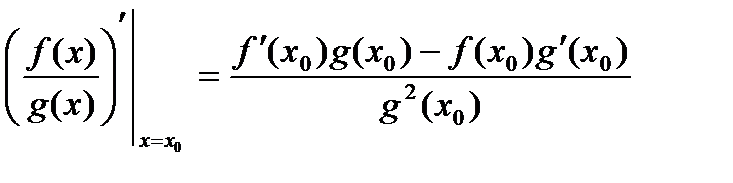 . (3)
. (3)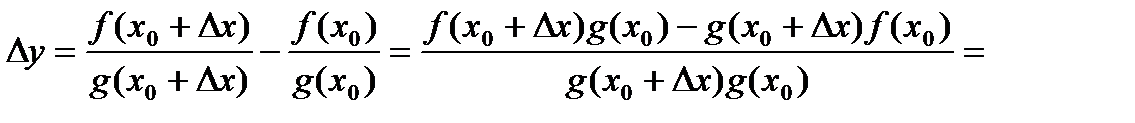

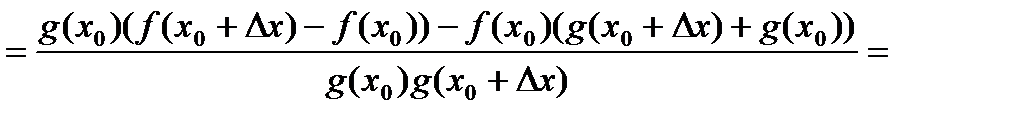
 ,
,
 .
.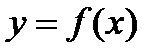 непрерывна и строго монотонна (строго монотонно возрастает или убывает) в некоторой окрестности точки
непрерывна и строго монотонна (строго монотонно возрастает или убывает) в некоторой окрестности точки  и в точке
и в точке  , тогда обратная функция
, тогда обратная функция 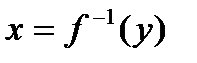 имеет производную в точке
имеет производную в точке 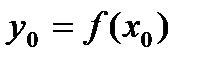 , причем
, причем .
. . Если
. Если  , то
, то 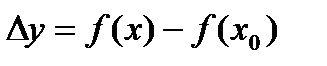 . В силу непрерывности функции
. В силу непрерывности функции  .
.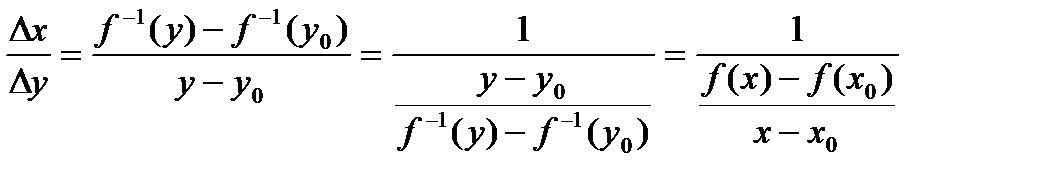 .
.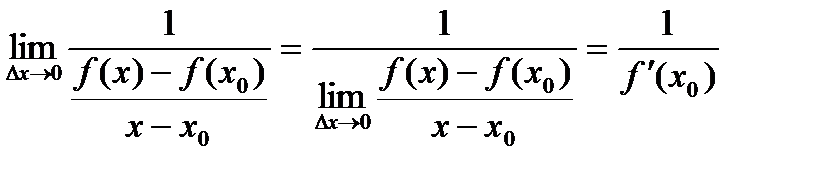 ,
, .
.


