
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия экстремума ТЕОРЕМА 1. Пусть функция
Доказательство. Пусть Если Если Получаем, что Замечание. В точке
если точка
если точка
ТЕОРЕМА 2. Пусть функция
Доказательство. Функция удовлетворяет условиям теоремы о разложении по формуле Тейлора с дополнительным членом в форме Пеано, то есть
Учитывая, что
По определению Пусть
Тогда в равенстве (2) правая часть строго меньше нуля, и и, следовательно, Если
Тогда в равенстве (2) правая часть строго больше нуля, и и, следовательно,
ОПРЕДЕЛЕНИЕ. Точка ТЕОРЕМА 3. Пусть функция Доказательство. Функция удовлетворяет условиям теоремы о разложении по формуле Тейлора с дополнительным членом в форме Пеано, то есть
Учитывая, что
По определению Пусть
Тогда в равенстве (3) правая часть строго меньше нуля, если и, следовательно, Если
Если
Тогда в равенстве (3) правая часть строго меньше нуля, если и, следовательно, Если Теорема доказана.
|
||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.157.186 (0.005 с.) |
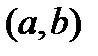 , кроме может быть точки
, кроме может быть точки 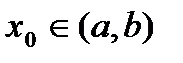 , в которой функция непрерывна. Если производная
, в которой функция непрерывна. Если производная  меняет знак при переходе через точку
меняет знак при переходе через точку 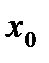 (то есть
(то есть  такое, что при
такое, что при  производная
производная  имеет один знак, а
имеет один знак, а  другой), то точка
другой), то точка  - точка строгого локального экстремума. При этом, если
- точка строгого локального экстремума. При этом, если 
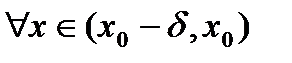 и
и 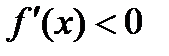
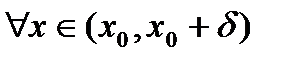 , то точка
, то точка 

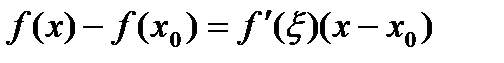 . (1)
. (1)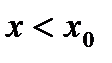 , то
, то 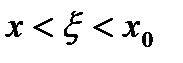 ,
,  ,
, 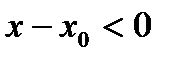 , тогда
, тогда 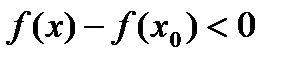 .
. , то
, то 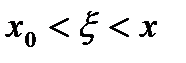 ,
,  ,
,  , тогда
, тогда 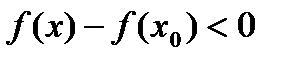 .
. выполняется неравенство
выполняется неравенство  . По определению это означает, что
. По определению это означает, что 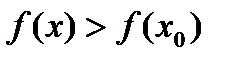 . По определению это означает, что
. По определению это означает, что  . На рисунках изображены случаи, если производная не существует (слева), и когда производная равна нулю,
. На рисунках изображены случаи, если производная не существует (слева), и когда производная равна нулю,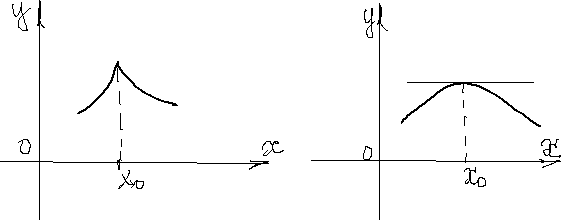

 дифференцируема на интервале
дифференцируема на интервале  имеет вторую производную, и
имеет вторую производную, и 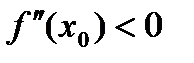 (или
(или  ), тогда
), тогда 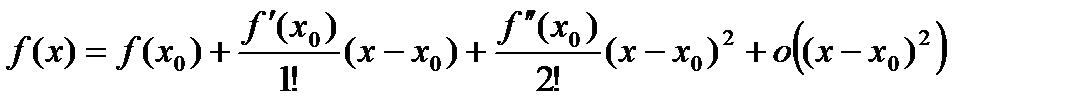 .
.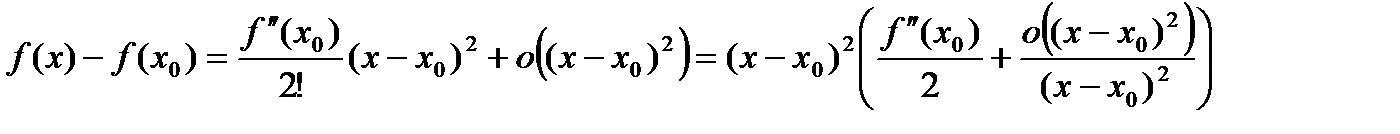 . (2)
. (2) , то есть
, то есть 
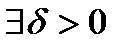 такое, что
такое, что 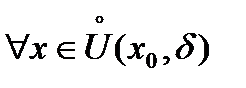 выполняется неравенство
выполняется неравенство  , или
, или  .
. , тогда
, тогда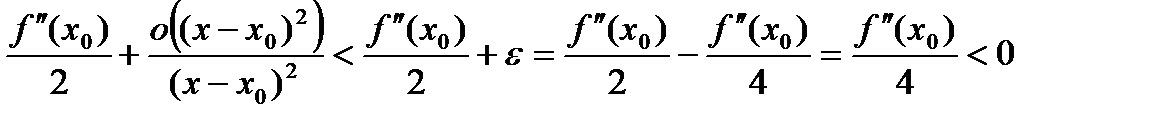 .
. ,
, , положим
, положим  , тогда
, тогда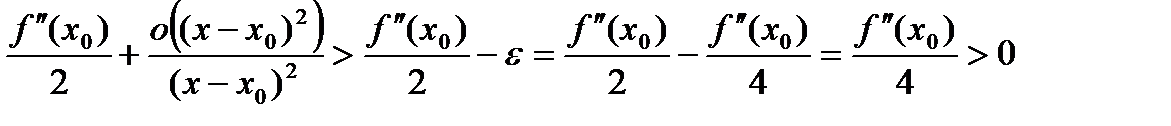 .
.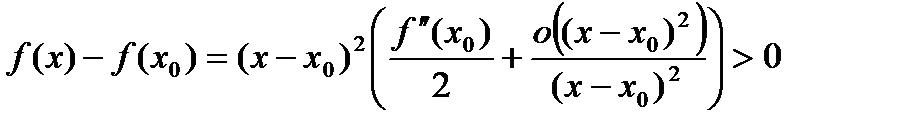 ,
, называется точкой возрастания (убывания) функции
называется точкой возрастания (убывания) функции 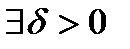
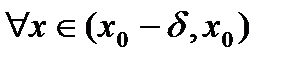 выполняется неравенство
выполняется неравенство  , а
, а 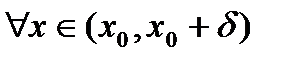 выполняется неравенство
выполняется неравенство  (
( , а
, а 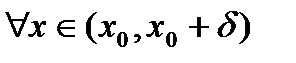 выполняется неравенство
выполняется неравенство  ).
). раз, в точке
раз, в точке 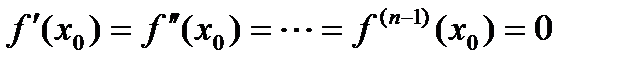 ,
,  . Тогда, если
. Тогда, если  - четное, то функция имеет в точке
- четное, то функция имеет в точке  и минимум, если
и минимум, если 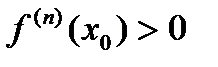 . Если же
. Если же 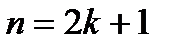 - нечетное число, то
- нечетное число, то  .
. . (3)
. (3) , то есть
, то есть 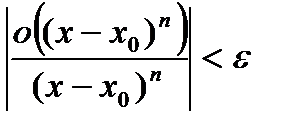 , или
, или 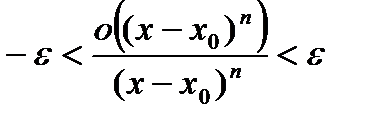 .
. . Положим
. Положим  , тогда
, тогда .
. ,
, меняет знак с «-» на «+» при переходе через точку
меняет знак с «-» на «+» при переходе через точку  , положим
, положим 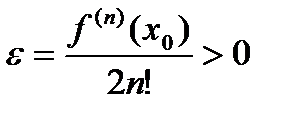 , тогда
, тогда .
.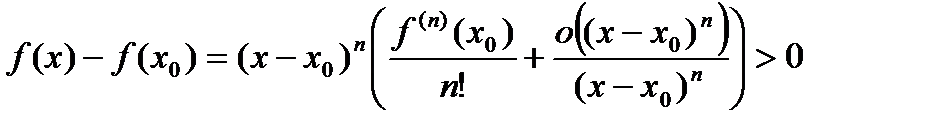 ,
, , а
, а 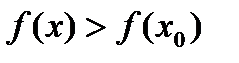 . Следовательно,
. Следовательно, 


