Параллельность прямых, прямой и плоскости

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Параллельность прямых, прямой и плоскости

 

Параллельность прямой и плоскости

Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:

1) прямая лежит (находится) в плоскости;

2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются);

3) прямая и плоскость не имеют общих точек.

 

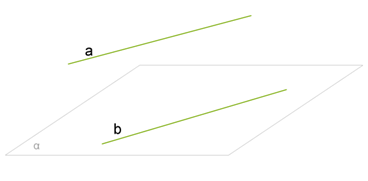
Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема 5 «Признак параллельности прямой и плоскости».

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

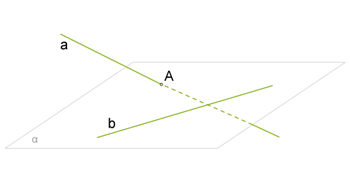
Доказательство:

доказательство проведём от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причём A не находится на b, так как a ∥ b. Согласно признаку скрещивающихся прямых, прямые a и b — скрещивающиеся.

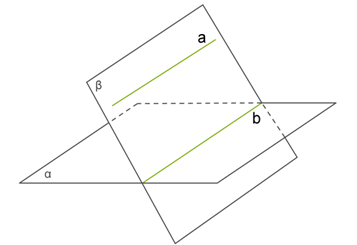
Мы пришли к противоречию. Так как согласно данной информации a ∥ b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Обрати внимание!

Следующие две теоремы очень часто используются при решении задач.

Теорема 6.

Если плоскость β проходит через данную прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b ∥ a.

Обрати внимание!

Прямую b иногда называют следом плоскости β на плоскости α.

Теорема 7.

Если одна из двух параллельных прямых a ∥ b параллельна данной плоскости α, то другая прямая либо параллельна этой плоскости, либо лежит в этой плоскости.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Взаимное расположение прямой и плоскости в пространстве

Условие задания:

Определи взаимное расположение данной прямой и плоскости.

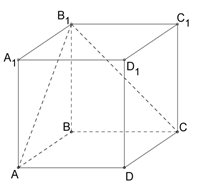
1. Прямая AA₁ и плоскость (ADD₁): прямая параллельна плоскости прямая находится в плоскости прямая пересекает плоскость.

2. Прямая BC и плоскость (A₁B₁C₁): прямая пересекает плоскость прямая находится в плоскости прямая параллельна плоскости.

3. Прямая CC₁ и плоскость (ABA₁): прямая параллельна плоскости прямая находится в плоскости прямая пересекает плоскость.

4. Прямая CB₁ и плоскость (DD₁C): прямая параллельна плоскости прямая пересекает плоскость прямая находится в плоскости.

5. Прямая AB₁ и плоскость (DD₁C): прямая параллельна плоскости прямая пересекает плоскость прямая находится в плоскости.

 

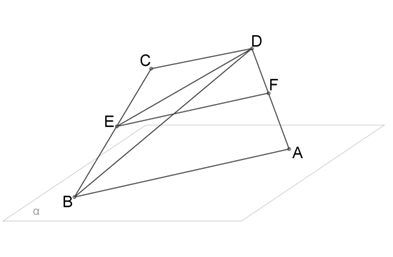
Прямая и плоскость

Условие задания:

Основание AB трапеции ABCD лежит в плоскости α. Основание CD не лежит в этой плоскости.

Дополни данные предложения, которые характеризуют взаимное расположение данных прямых и плоскости α.

1.Tак как прямая DB имеет общую точку с данной плоскостью, то эта прямая параллельна плоскости находится в плоскости пересекается с плоскостью  α.

2.Средняя линия EF трапеции параллельна основаниям, поэтому она находится в плоскости параллельна плоскости пересекается с плоскостью  α.

 

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Параллельность прямых, прямой и плоскости