
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
График четной функции является симметричным относительно оси ОУ .Содержание книги
Поиск на нашем сайте
Если же функция f является нечетной, то графику функции одновременно принадлежат точки с координатами график нечетной функции является симметричным относительно начала координат О. Заметим, что всякую функцию, которая задана на симметричном множестве, можно представить в виде суммы четной и нечетной функций. В самом деле, пусть f задана на симметричном множестве Х. Тогда Очевидно, Функция Функция
Множество точек плоскости,удовлетворяющих уравнению j (x, y)=0, называется графиком этого уравнения.
К примеру, уравнение j (x, y)= Периодические функции. Многие явления в природе и технике являются повторяющимися во времени (периодичными)процессами. Например, движение стрелок часов, планет, приливы, электромагнитные волны и др.Изучение указанных явлений приводит нас к периодическим функциям. Функция 1) 2) График периодической функции изображен на рисунке. Легко показать, что, если T >0 есть период заданной функции, то всякое число вида kT, где k – целое число, также является периодом этой функции. Действительно,=f((x+T)+T)=f(x+T)=f(x), так как Для построения графика периодической функции достаточно построить его на любом отрезке длины Т. Выполняя параллельный перенос графика на Т единиц влево и вправо вдоль оси ОХ, получим весь график функции. Так функции являются периодическими с периодом равным Периодические функции обладают следующими свойствами: 1. Если Т – период функции f (x), то функция Действительно,
Так, функция 2. Если периоды В самом деле,пусть отрезки длины Найдем период функции у= Sin 2 x + Cos 3 x. Период функции Sin 2 x равен 4.Монотонные функции. Функция Заметим, что неубывающая и невозрастающая функции могут принимать в различных точках равные значения. (см. рис. 23 и 25). Возрастающая функция характеризуется тем, что из любых двух точек на графике правая лежит выше левой, т.е. при движении слева направо график функции поднимается (см. рис. 22). Если же функция убывающая, то ее график при движении слева направо график функции опускается (см. рис. 24). Для неубывающей функции график не опускается (рис. 23), для невозрастающей – не поднимается (рис. 25). Функции, удовлетворяющие любому из указанных выше условий, называются монотонными. При этом возрастающие и убывающие функции называются строго монотонными (или монотонными в «строгом смысле»), а неубывающие и невозрастающие функции называются монотонными «в широком смысле». ункция называется кусочно-монотонной, если область ее определения можно разбить на «части», на которых она монотонна. Так, функция является кусочно-монотонной на R. В самом деле, множество R разобъем на две «части» Вопросы и задания для самопроверки. 1. Приведите определение функции, области определения и области изменения функции. 2. Определяет ли формула 3. Определяет ли формула 4. При каких условиях формула 5. Приведите определение четной и нечетной функций. 6. Можно ли всякую функцию представить в виде суммы четной и нечетной функций? 7. Может ли быть четной (нечетной) сумма, разность, произведение и частное четной и нечетной функций? Приведите примеры. 8. Приведите определение периодической функции. 9. Всегда ли сумма (разность) двух периодических функций является периодической функцией? 10. При каких условиях сумма (разность) двух периодических функций является периодической функцией? 11. Является ли произведение двух периодических функций периодической функцией? Приведите примеры. 12. Приведите определения возрастающей, неубывающей, убывающей, невозрастающей функций. Приведите примеры. 13. Всегда ли сумма двух возрастающих (убывающих) функций является возрастающей (убывающей) функцией? Приведите примеры. 14. Что можно сказать о характере монотонности суммы убывающей и возрастающей функций? Приведите примеры. 15. Что можно сказать о характере монотонности произведения (частного) двух монотонных функций? Приведите примеры. 16. Найдите область определения функций: 1. 4. 7. 10. 13. 16. 19. 17. Исследовать на четность функции: 1. 4. 7. 10. 13. Доказать, что функция
4. 7. 10. 20. Приведите примеры функций, имеющих следующие периоды: 1) 21. Найти период функции Решение. Функция 22. Доказать, что функция Решение. Пусть 23. Докажите, что указанные ниже функции являются строго монотонными на указанных промежутках: 1. 4. 7. 10. 24. Найти промежутки монотонности функций: 1. 4. 7. 25. Являются ли кусочно-монотонными следующие функции: 1. 4. 6. 25.Являются ли кусочно-монотонными следующие функции: 1. 4. 6.
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.54 (0.009 с.) |

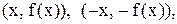 это означает, что
это означает, что

 , т.е.
, т.е. 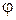 является четной функцией,
является четной функцией, 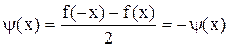 , т.е.
, т.е. 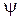 – нечетная функция.
– нечетная функция. представляет пример четной функции, т.к.
представляет пример четной функции, т.к.  для любого действительного числа х. Так как
для любого действительного числа х. Так как  , то функция знака
, то функция знака 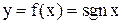 является нечетной.
является нечетной. , заданная на всей числовой оси, не является ни четной, ни нечетной (почему?). Представим ее в виде суммы четной и нечетной функций. Имеем:
, заданная на всей числовой оси, не является ни четной, ни нечетной (почему?). Представим ее в виде суммы четной и нечетной функций. Имеем: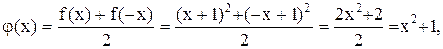
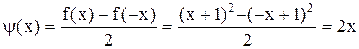 . Очевидно,
. Очевидно,  является четной функцией, а
является четной функцией, а  – нечетной функцией. Значит,
– нечетной функцией. Значит, 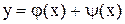 .
. Если j (- x, y)= j (x, y), то график уравнения симметричен относительно оси ординат, если же j (x,- y)= j (x, y), то он симметричен относительно оси абсцисс, при выполнении условия j (- x,- y)= j (x, y) график будет симметричным относительно осей координат (почему?).
Если j (- x, y)= j (x, y), то график уравнения симметричен относительно оси ординат, если же j (x,- y)= j (x, y), то он симметричен относительно оси абсцисс, при выполнении условия j (- x,- y)= j (x, y) график будет симметричным относительно осей координат (почему?). 0 удовлетворяет условию j (- x,- y)= j (x, y), так как
0 удовлетворяет условию j (- x,- y)= j (x, y), так как 
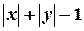 по свойству модуля,и,значит, график этого уравнения симметричен относительно осей координат.Для постоения графика достаточно построить его часть,расположенную в первой четверти,а затем зеркально отобразить эту часть относительно осей координат. В первой четверти j (x, y)=х+у-1=0, и графиком уравнения будет часть прямой,которая находится в первой четверти.
по свойству модуля,и,значит, график этого уравнения симметричен относительно осей координат.Для постоения графика достаточно построить его часть,расположенную в первой четверти,а затем зеркально отобразить эту часть относительно осей координат. В первой четверти j (x, y)=х+у-1=0, и графиком уравнения будет часть прямой,которая находится в первой четверти.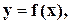 определенная на множестве Х, называется периодической с периодом T >0, если выполняются условия:
определенная на множестве Х, называется периодической с периодом T >0, если выполняются условия: если то и
если то и  ;
;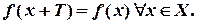

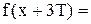
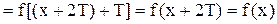 , и т.д. Аналогично: f(x-T)=f((x-T)+T)=f(x), так как
, и т.д. Аналогично: f(x-T)=f((x-T)+T)=f(x), так как 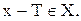

 , и т.д. Наименьший положительный период функции f называется ее основным периодом. Для постоянной функции любое число
, и т.д. Наименьший положительный период функции f называется ее основным периодом. Для постоянной функции любое число  является периодом. Однако, она не имеет основного периода, так как во множестве действительных положительнвых чисел нет наименьшего числа.
является периодом. Однако, она не имеет основного периода, так как во множестве действительных положительнвых чисел нет наименьшего числа.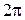 , а функции
, а функции 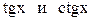 -периодическими с периодом равным
-периодическими с периодом равным 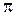 .
. имеет период равный
имеет период равный  .
. .
.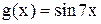 имеет период равный
имеет период равный  , т.к. функция
, т.к. функция  имеет период
имеет период  , а
, а 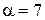 .
. соответственно функций
соответственно функций 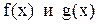 соизмеримы, то сумма (разность), произведение этих функций являются периодическими функциями.
соизмеримы, то сумма (разность), произведение этих функций являются периодическими функциями.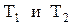 соизмеримы, т.е.
соизмеримы, т.е. 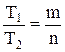 , где m и n – натуральные числа. Тогда
, где m и n – натуральные числа. Тогда  . Рассмотрим функцию
. Рассмотрим функцию 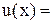
 и докажем, что она является периодической с периодом
и докажем, что она является периодической с периодом 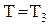 . Имеем:
. Имеем: 
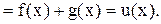 Свойство 2 доказывается таким же способом для разности и произведения функций.
Свойство 2 доказывается таким же способом для разности и произведения функций. , а функции Cos 3 x равен
, а функции Cos 3 x равен 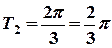 по свойству 1.Далее,
по свойству 1.Далее,  т.е.
т.е.  Следовательно, периодом данной функции будет число Т=2p. Функция у= Sin
Следовательно, периодом данной функции будет число Т=2p. Функция у= Sin 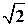 x + Cos 3 x не является периодической,так как отношшение периода первой функции
x + Cos 3 x не является периодической,так как отношшение периода первой функции 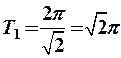 к периоду второй
к периоду второй  иррациональное число.
иррациональное число. и
и 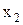 из Х, таких, что
из Х, таких, что  ,неубывающей, если для любых
,неубывающей, если для любых 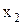 из Х, таких, что
из Х, таких, что  <
<  , выполняется неравенство
, выполняется неравенство  ,убывающей, если для любых
,убывающей, если для любых 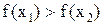 ,невозрастающей, если для любых
,невозрастающей, если для любых  .
.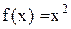 является кусочно-монотонной на R. В самом деле, множество R разобъем на две
является кусочно-монотонной на R. В самом деле, множество R разобъем на две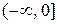 ,
, 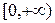 . На промежутке
. На промежутке  также являются кусочно-монотонными на R.
также являются кусочно-монотонными на R.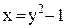 переменную х как функцию переменной у? Найдите
переменную х как функцию переменной у? Найдите  . Постройте график данной функции.
. Постройте график данной функции. переменную у как функцию переменной х?
переменную у как функцию переменной х?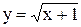 ? Функцию
? Функцию  ? Постройте графики этих функций.
? Постройте графики этих функций.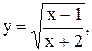 2.
2. 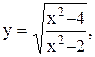 3.
3. 
 5.
5.  6.
6. 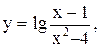
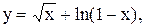 8.
8.  , 9.
, 9. 
 11.
11.  12.
12. 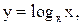
 14.
14. 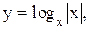 15.
15. 
 17.
17.  18.
18. 
 20.
20. 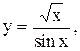 21.
21. 
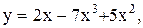 2.
2.  3.
3. 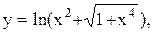
 5.
5.  6.
6. 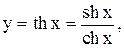
 8.
8. 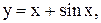 9.
9. 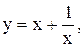
 11.
11. 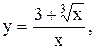 12.
12. 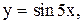
 14.
14. 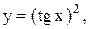 15.
15. 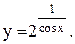
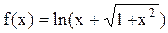 является нечетной. Решение. Подставляем -х вместо х в выражение для f(x):
является нечетной. Решение. Подставляем -х вместо х в выражение для f(x): 5.
5.  6.
6. 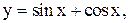
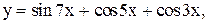 8.
8.  9.
9. 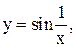
 11.
11.  12.
12. 
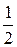 , 2)
, 2) 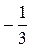 , 3)
, 3) 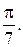
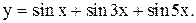
 имеет период
имеет период  , функция
, функция  – период
– период  , функция
, функция  – период
– период  . В соответсвии со свойством 2 периодических функций наша функция является периодической с периодом
. В соответсвии со свойством 2 периодических функций наша функция является периодической с периодом 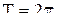 , т.к. отрезки
, т.к. отрезки  ,
,  .
.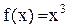 строго возрасает на множестве R.
строго возрасает на множестве R. – произвольные числа, причем
– произвольные числа, причем 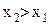 . Покажем, что
. Покажем, что 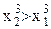 . Для этого рассмотрим разность
. Для этого рассмотрим разность 
 т.к. все сомножители в правой части положительны.
т.к. все сомножители в правой части положительны.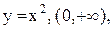 2.
2. 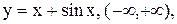 3.
3. 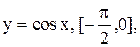
 5.
5.  6.
6. 
 8.
8. 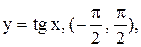 9.
9. 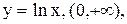
 11.
11. 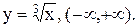
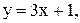 2.
2. 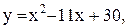 3.
3. 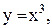
 5.
5. 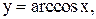 6.
6. 
 8.
8. 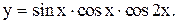
 2.
2.  3.
3. 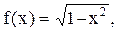
 5.
5. 
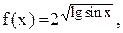 7.
7. 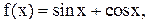 8.
8. 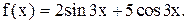
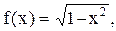
 5.
5. 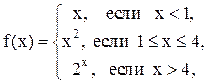
 8.
8. 


