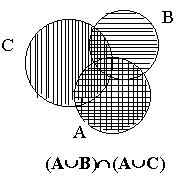Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
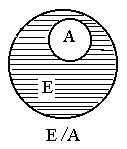
Множество, состоящее из элементов, принадлежащих одновременно множеству А и множеству В, называется пересечением множеств А и ВСодержание книги
Поиск на нашем сайте
Очевидно, что А Ç А=А; если А Ì В, то А Ç В=А. Операция пересечения множеств переносится на любое число множеств. Пересечением любого числа множеств считается множество, состоящее из элементов, принадлежащих одновременно каждому из заданныхмножеств. Для рассмотренных выше множеств А Ç В Ç С= Æ. Пересечение множеств Q и множества всех иррациональных чисел есть пустое множество, так как любое рациональное число не является иррациональным числом.
Очевидно, А\А= Æ; если В Ì А, то В\А= Æ. Разность множества действительных и иррациональных чисел есть множество рациональных чисел Q. Дополнением А Ì Е множества А до множества Е называется множество АC, состоящее из всех элементов множества Е, не принадлежащих множеству А, то есть АC=Е\ А. Очевидно, А Ç АC= Æ. Например, дополнением множества Q до множества R является множество всех иррациональных чисел. Вопросы для самопроверки. Что такое объединение множеств? Разность множеств? 2. Приведите примеры объединения множеств. Что такое пересечение множеств? 4. Приведите примеры пересечения множеств. Что такое дополнение к множеству? 6. Приведите примеры дополнения к множеству. Упражнения. 1. Доказать, что А È (В Ç С)=(А È В) Ç (А È С). ешение. Пусть элемент х входит в левую часть равенства. Тогда х Î А или х Î В Ç С. Если х Î А, то х Î А È В и х Î А È С, следовательно, х принадлежит правой части доказываемого равенства. Если же х Î В Ç С, то х Î В и х Î С. Но тогда х Î А È В и х Î А È С. Значит, и в этом случае х является элементом правой части. Обратно, пусть теперь х есть элемент правой части. Значит х Î А È В и х Î А È С. Если х Î А, то х Î А È (В Ç С). Если же х не принадлежит А, то х Î В и х Î С. Значит, х Î В Ç С, и опять х принадлежит левой части.
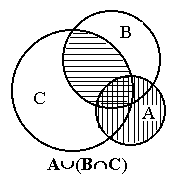
На левом рисунке множество А È В заштриховано горизонтальной штриховкой, а множество А È С - вертикальной штриховкой. Множество (А È В) Ç (А È С) изображено квадратной штриховкой. На правом рисунке множество В Ç С изображено горизонтальной штриховкой, а множество А - вертикальной штриховкой. Заштрихованная область дает множество А È (В Ç С). Мы получили геометрическое доказательство, так как множество, заштрихованное на левом рисунке квадратной штриховкой, и множество, заштрихованное на правом рисунке, совпадают. 2. Доказать, что А È В=В È А (свойство коммутативности объединения множеств). 3. А Ç В=В Ç А (свойство коммутативности пересечения множеств). Доказать. 4. (А È В) È С=А È (В È С) (свойство ассоциативности объединения множеств). Доказать 5. Доказать, что (А Ç В) Ç С=А Ç (В Ç С)= А Ç В Ç С (свойство ассоциативности пересечения множеств). 6. Убедиться, что три соотношения А Ì В, А Ç В=А, А È В=В равносильны, то есть, что из выполнения любого из них вытекает справедливость остальных двух. 7. Верно ли равенство А Ç В=А\(A\B)? 8. (A\B)\C=A\(B È C). Доказать. 9. Верно ли соотношение (A\B) Ç (C\D)=(A Ç C)\(B Ç D)? 10. Доказать, что условие (A È B)\B=A выполняется в том и только том случае, когда A Ç B= Æ. 11. (A\B) È B=A Û B Ì A. Доказать. 12. Доказать, что операции È и Ç связаны законами дистрибутивности: (A È B) Ç C=(A Ç C) È (B Ç C), (A Ç B) È C=(A È C) Ç (B È C), 13. Если A Ì B, то A È B=B? 14. A È Æ =A? 15. Если A Ì B, A Ç B=A? 16. Доказать, что A=B, если A Ì B и B Ì A. 17. Если A Ì B и B Ì C, то A Ì C. Доказать. 18. Следует ли из A Ç B=A соотношение A Ì B? 19. Вытекает ли из A\B=С, что А=B È C? 20. Вытекает ли из A=B È C, что A\B=C? 21. Верно ли, что A\(B È C)=(A\B)\C? 22. A È (B\C)=(A È B)\C? 23. (A\B) È C=(A È C)\B?
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.009 с.) |

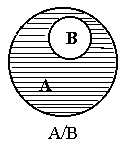 Разностью множеств А и В называется множество А\В, элементы которого принадлежат множеству А, но не принадлежат множеству В.
Разностью множеств А и В называется множество А\В, элементы которого принадлежат множеству А, но не принадлежат множеству В.